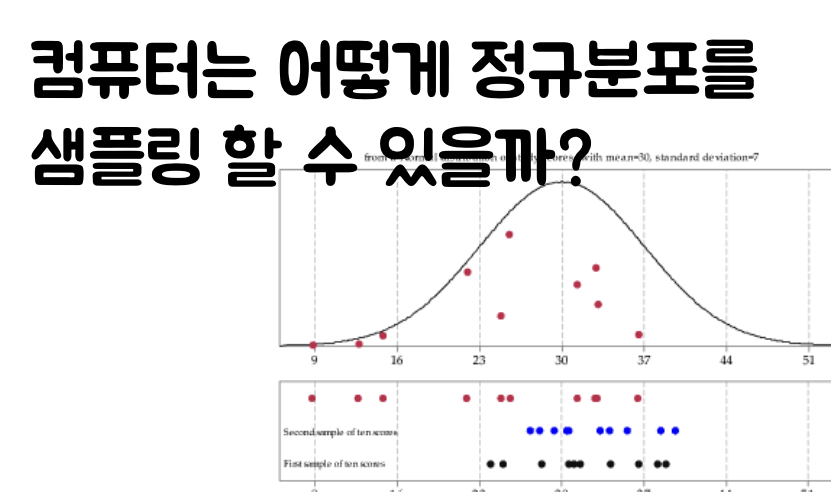
1. Intro
- 일단 uniform하게 0~1사이의 숫자를 뽑을 수 있다고 가정하자.
- 선형합동 or 메르센 트위스터 참고
- uniform 분포로 부터 정규분포(or 감마, 베타 등등 다양한 분포)를 어떻게 하면 생성해낼 수 있을까?
- 컴퓨터는 uniform 분포를 뽑는 방법을 기반으로 이후 다른 다양한 분포를 uniform 기반으로 생성해 낸다.
- 다양한 확률분포를 생성해낼 수 있는 Inverse sampling에 대해서 알아보자
2. Inverse Sampling - intuitive understanding
- 우리가 뽑고 싶은 분포의 pdf가 다음과 같다고 가정해보자.
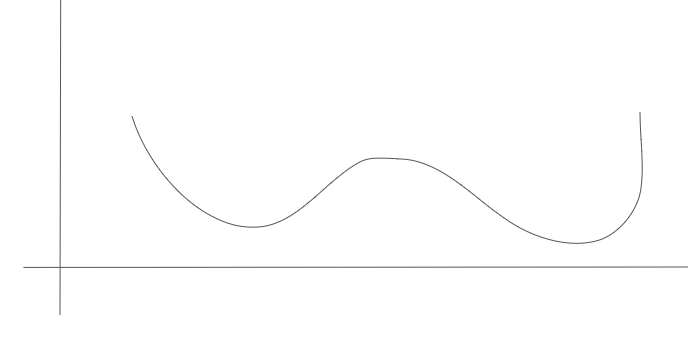
-
위 pdf를 9개의 구간으로 나눠보자
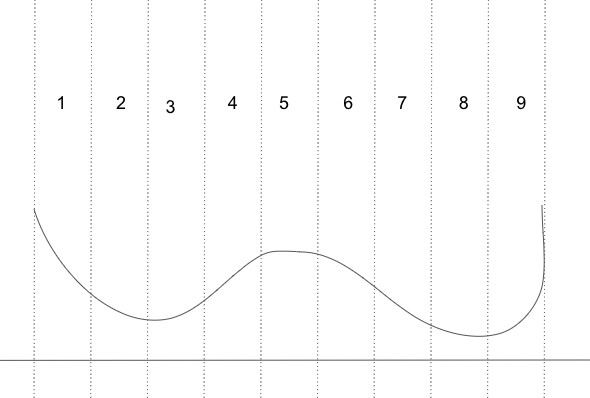
-
각 구간의 확률이 서로 다른데 3번 구간 보다 5번 구간이 더 높은 확률로 뽑힐 것이다.
-
각 구간이 뽑힐 확률이 동일하도록 다시 구간별 넓이를 조정해보자!
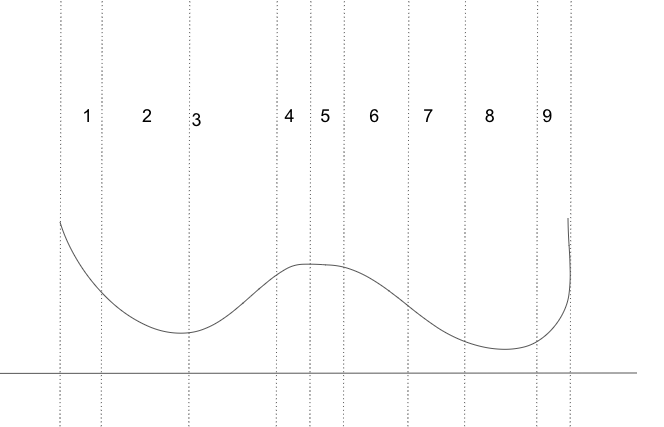
-
이제 각 구간이 뽑힐 확률이 동일하다!
-
위 pdf에서 x를 임의로 추출했을 때 해당 x가 특정 블락(예를 들면 3번)에 있을 확률은 1/9일 것이다.
-
만약 위 블락 1000만개라면...?
- 확률은 1/1000만 일 것이다
-
그렇다면 균등한 확률을 가지는 9개의 숫자 중 (1,2,3,4,5,6,7,8,9)하나의 숫자를 뽑는 것과 블락에서 숫자를 뽑는것과 분포는 다를 것이 없다.
-
9개의 숫자 중 하나를 뽑은 후 뽑힌 숫자에 해당하는 블락의 대표값으로 대체하면 어떤일이 우리는 대충 "근사하게" pdf를 흉내내면서 샘플링을 할 수 있을 것이다.
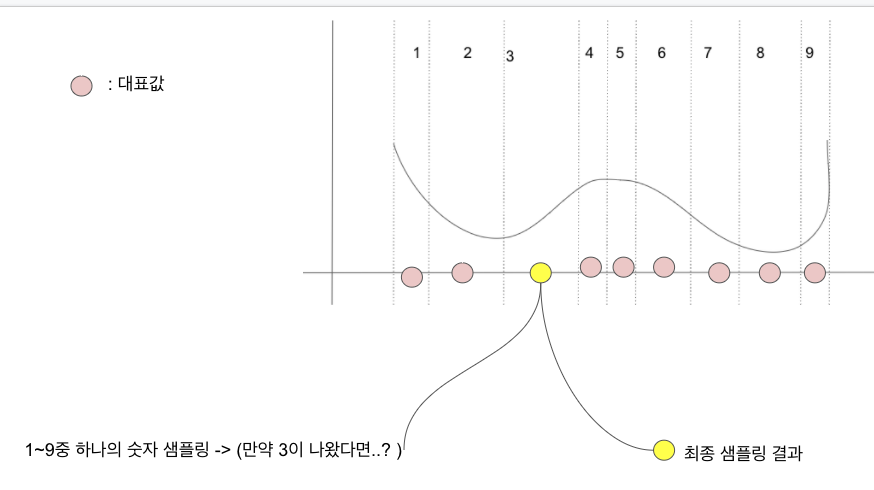
-
아래 처럼 구역을 나눌수록 이 방법은 정교해지고 실제 pdf를 따라 할 수 있을 것이다.
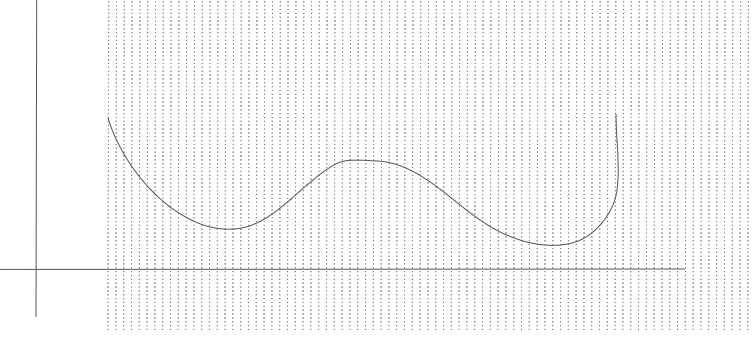
3. Inverse Sampling - mathematical approach
- 위 방법을 좀더 수학적으로 아름답게? 접근해보자.
- 구역을 무한개로 쪼갰다고 생각해보고, 0~1사이의 실수 하나를 Uniform 분포에서 뽑아보자.
- 그러면 그 값에 해당하는 "구역"은 어떻게 찾을 수 있을까?
3-1 CDF
- 이번에는 Y축을 정확히 똑같이 9등분을 해보자 그후 아래 처럼 각 네모칸이 만나는 점을 기준으로 선을 그어보자
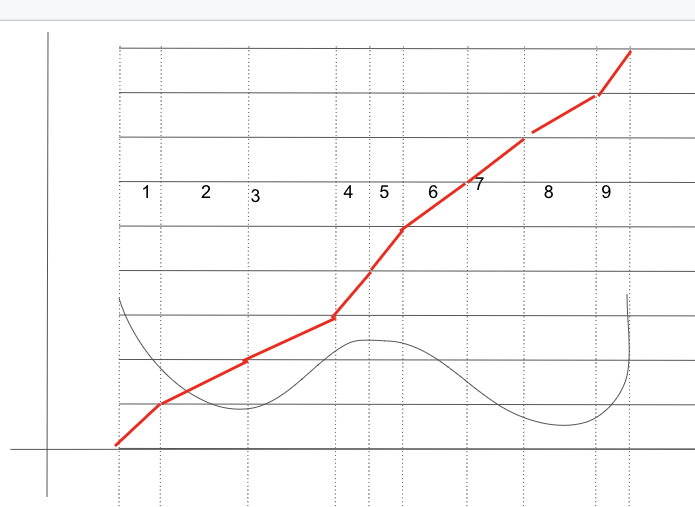
- 그러면 Y축을 기준으로 쪼개진 영역중 하나를 선택후 그에 해당하는 X축 영역을 선택하면 위 2번에서 했던 방법을 똑같이 따라하게 된다.
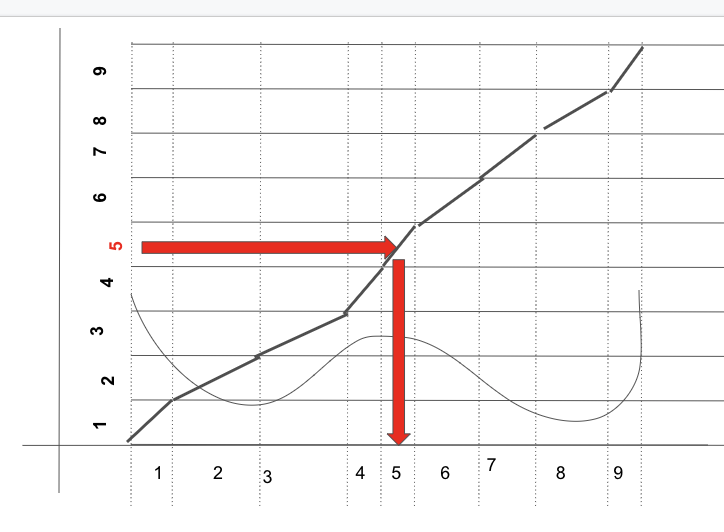
- 마찬가지로 Y축과 X축을 1000만개로 쪼개고 무한개로 쪼개면 어떻게 될까?
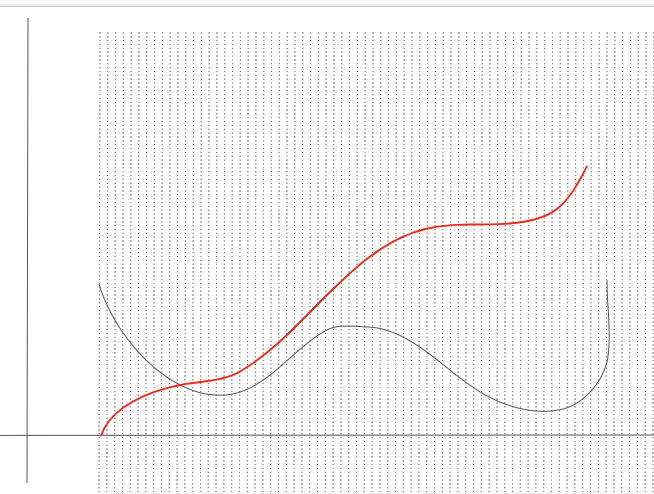
- 네모칸을 이어 그린 곡선은 CDF가 된다!!
3-2 inverse CDF
- 그러면 Y축에서 0~1사이의 값을 랜덤하게 뽑은 해당 영역에 해당하는 X의 값을 뽑는 행위는 무엇이 될까?
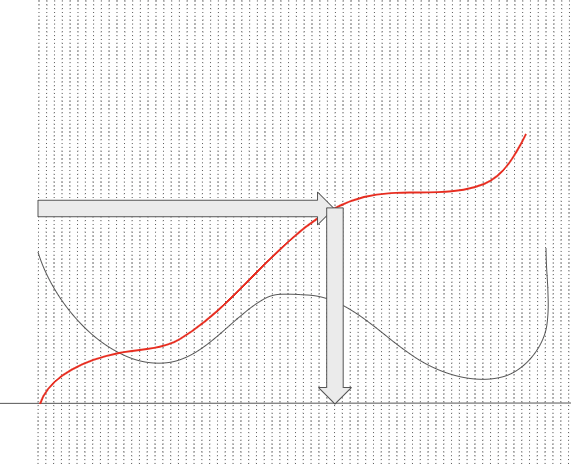
- 바로 CDF의 역함수의 값이 된다.
- 즉 어떤 수 가 의 분포에서 뽑았다고 가정해보자.
- 그리고 우리가 원하는 pdf를 , 그 pdf의 CDF(빨간선)를 라고 해보자.
- 그러면 에 대응하는 블록은 가 된다.
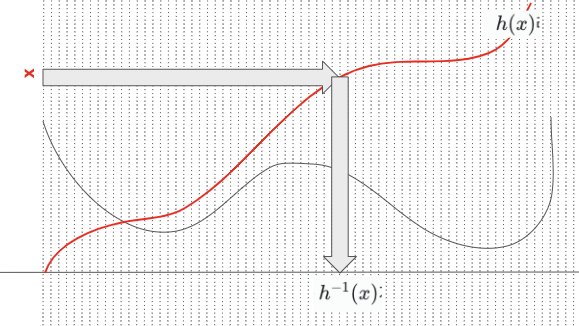
4 Inverse CDF 정리
- Uniform(0,1)로 부터 하나의 숫자 x를 뽑는다.
- 선형합동 or 메르센 트위스터 참고
- cdf의 역함수로 부터 숫자를 추출해낸다:
- 는 우리가 원하는 pdf로 부터 샘플링한 숫자가 된다.