
1. WHY Mutual Information Estimation?
1-1 Pearson correlation coefficient
- 상관계수는 두 변수 사이의 '상관관계'를 계량화한 수치이다.
- 상관계수는 측정하는 방식에 따라 매우 다양하지만, 우리가 보통 상관계수라고 부르면 맥락상
Pearson correlation coefficient을 뜻 한다. Pearson correlation coefficient은 기초 통계학시간에 배우는 지표로 두 확률변수의 공분산 값을 두 확률변수 각각의 표준편차로 나눠준 값이다.- 피어슨 상관 계수 = (X,Y)공분산/(X 표준편차 * Y 표준편차)
1-2 Pearson correlation coefficient 한계
- 본래 '상관계수'는 두 변수의 상관관계를 계량화한 수치이다.
- 때문에, 두 변수에 뚜렷한 관계가 있다면, 그 관계가 non-linear하든 linear 그 두 변수 사이의 관계를 잘 반영할 수 있어야 한다.
- 하지만
Pearson correlation coefficient는 linear한 관계만 잘 측정하고, non-linear한 관계는 잘 반영하지 못 한다. - 아래 그림은 분포에 따른
Pearson correlation coefficient로 분명 상관관계가 있음에도 non-linear할 경우 값이 0이 된다.

- 또한 pearson 상관계수는 두확률변수 사이만 가능할 뿐 (X,Y <-> Z,H) 와 같이 여러개의 두 확률벡터간의 상관계수는 측정할 수 없다.
1-1-3 Mutual Information
- mutual information은 피어슨 상관 계수와 마찬가지로 두 변수 사이의 상관관계를 측정할 수 있다.
- 아래 그림의 MIC는 mutual information 값을 나타내는데, 두 변수사이의 non-linear한 관계 또한 잡아낼 수 있는 것을 볼 수 있다.

- 두 확률변수 사이의 관계를 정보이론 관점에서 겹치는 정보량을 계량 할 수 있다.
- 아래는 mutual information을 계산하는 식이다. mutual information에 대한 자세한 내용은 정보이론을 배우면 알 수 있다.
1-4 Feature selection
- feature selection을 할 때 Y와 상관계수가 높으면서 feature들 끼리는 상관계수가 작기를 원한다.
- 그래서 피어슨 상관 계수를 EDA 단계에서 많이 확인한다.
- feature 선택을 할 때는 아마 아래와 같은 상황을 원할 것이다.
- 종속변수와 독립변수들의 상관계수를 높인다.
- 독립변수 사이의 상관계수를 낮춘다.
- 다중공선성(독립변수들 간에 강한 상관관계가 나타나는 문제)가 안 나타난다.
- 상관계수를 완벽하게 "추정"만 할 수 있다면 피어슨 상관계수보다 이론적으로 완벽한 mututual information을 쓰는게 더욱 좋을 것이다.
- Mutual information은 또한 (Y <-> X1,X2,X4) 와 같이 여러개의확률벡터간의 상관계수도 측정할 수 있다.
- ex : (X1,X2<-> X1,X2,X4)
- ex : (Y <-> X1,X2,X4)
- ex : (X1<-> X2,X4)
1-5 mutual information Estimation
- mutual information은 추정하는 방법이 어렵고, 또 정확하지 않아서 잘 안 쓰이고 있는 것 같다.
- 그럼에도 불구하고 mutual information은 non-linear한 상관계수를 계량할 수 있다.
- feature selection, decision tree, 최적화, 무선통신 등 다양한 분야에서 mutual information은 ML연구에서 쓰이고 있다.
- 쓰이는 곳들 정리된 페이지: https://en.wikipedia.org/wiki/Mutual_information#Applications_2
2. Mutual Information Estimation 방법들
- mutual information식을 보면
- 3개 전부를 알아야 쓸 수 있다.
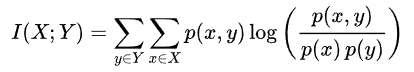
- 가장 간단하게 예측하는 방법은 binning method로 구획을 나누고 단순 카운트를 하여 빈도 예측하여 Mutual information을 구한다.
- 이 방법은 구획을 나누어 histogram을 구하기 때문에 binning으로 불리며 데이터가 많이 필요하다..
- 확률 분포 추정 시 bin 개수가 작으면 bin의 넓이가 커진다. 확률분포가 뭉개져 bin에서의 확률은 정확하지만 분포의 해상도는 작아진다.
(systematic error가 늘어남, statistical error는 줄어듬) - 확률 분포 추정을 bin 개수가 늘어나면, 분포의 해상도는 높아지지만 추정된 확률은 정확하지 않다.
(systematic error가 줄어듬, statistical error는 늘어남)
- 확률 분포 추정 시 bin 개수가 작으면 bin의 넓이가 커진다. 확률분포가 뭉개져 bin에서의 확률은 정확하지만 분포의 해상도는 작아진다.
- 데이터가 많아져서 p(x,y)를 정확하게 알게 되었다는 것은 확률분포를 이미 정확하게 알기 때문에 supervised learning의 목적인 P(Y|X)를 알 수 있게 되어 이런 과정이 필요 없는 상황일 가능성이 높다.
- 따라서 p(x,y)의 정확한 추정 없이 mutual information 추정 방법이 필요하다.
2-1 KSG Estimator (2004)
- 요즘 핫한 딥러닝 쪽 연구가 아님에도 무려 인용수가 2000회를 넘긴 Mutual information estimation 쪽의 시조새 같은 2004년도 연구가 있다.
- 이 연구로 부터 mutual information estimation은 쓸모 있어졌고, 그 후 연구도 대부분은 이 방법을 계량 시킨 것 들이다.
- A. Kraskov, H. Stogbauer and P. Grassberger, “Estimating mutual information”.Phys. Rev. E 69, 2004.

- 이 연구의 저자의 이름이 각자 Kraskov, Stogbauer, Grassberger인데 앞글자인 K,S,G를 가져와서 KSG Estimator라고 불린다.
- 이 논문을 읽는데 거의 일주일이 걸렸었는데, 지금 다시 보니까 너무 어렵고 기억이 잘 안 난다..
- 아래는 한 부분을 캡쳐해왔는데, 나의 그릇(실력?)으로는 도저히 요약이 불가능하다. 다음에 기회가 있으면 포스팅을 해보는 것으로...

- 여기 단락은 그냥 기억나는거 나불대는.. 자세히 읽지는 마세용..
- 대충 기억하기로 핵심은 데이터 포인트 들을 hyper-cube 상에서 구획을 나누어서 hyper cube별로 분포를 구해 도함수를 얻어 뭔가 적분을 해 mutual information 값을 얻었다..
- 아래 그림이 핵심이 였는데, X,Y축 구획을 나누어서 확률 분포 결합확률분포의 도함수를 추정해내는 걸로 기억한다..
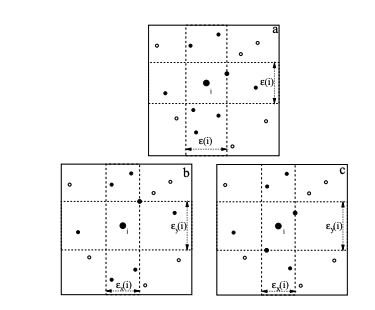
- 2004년에 나온 이 방법은 아직도 scikit learn에서 쓰이고 있는 방법이다.
2-2 이산확률변수는? (2014)
- KSG estimator는 두 확률변수가 모두 연속일 경우를 가정하고 있다.
- 따라서 확률변수가 만약 discrete 하다면 위 방법을 적용할 수가 없는데, 그러면 3개를 counting 하여 예측해야한다.
- 이 방법은 정확성이 떨어지고 실용성이 없는 문제가 있었다.
- 이후 이러한 문제를 해결하기 위해 등장한 연구가 아래 논문이다.
- B. C. Ross “Mutual Information between Discrete and Continuous Data Sets”. PLoS ONE 9(2), 2014.
- KSG Estimator처럼 특별한 명칭은 없었던 것 같다.
- 이 방법은 위 방법에서 생각하지 못한 이산확률변수 <-> 연속확률 변수 사이의 mutual information 계산을 위헤 nearest neighbor를 구하는 방법을 통계적 계산에 맞게 수정하여 정확도를 높였다.
- 이 방법 또한 scikit learn에서 쓰이며 discrete 옵션에 따라 정보를 알려주면 mutual information 추정이 방식으로 작동한다.
2-3 Mixed 확률변수는?(2017)
- Mixed Random variable
- https://www.probabilitycourse.com/chapter4/4_3_1_mixed.php
- 확률변수는 이산, 연속 2개의 타입만 있는 것이 아니다.
- 이산과 연속이 합쳐진 mixed 타입이 있다.
- 예를들어 씨앗을 심고 5일 후 새싹의 높이를 확률변수로 나타내었는데, 씨앗이 죽어버리면 0으로 나타내고 살아 있으면 높이를 나타낸다고 해보자.
- 죽어버릴 확률이 0.5이고 죽지 않았다면 씨앗의 높이가 0~1사이에서 살아있다는 조건부 uniform 분포를 그린다면 이 확률 변수는 이산적인 특성과 연속적인 특성이 함께 존재하게 된다.
- 이산일때는 합, 연속일때는 보통 적분으로 확률을 구하는 것을 넘어서
연속일때와 이산 그리고 mixed일때를 모두 일반화한 적분이 존재한다.
- 문제는 위에서 소개된 mutual information 추정 방법들이 모두 이산, 또는 연속 두 경우를 가정하고 있다.
- 따라서 mixed random variable일 경우에는 정확성이 떨어진다.
- 이러한 경우를 해결하기 위해 측도론에서 쓰는 일반적인 적분을 가져와 KSG estimator의 아이디어를 발전시킨 연구가 NIPS에 나왔다.
- Gao, Weihao, et al. "Estimating mutual information for discrete-continuous mixtures." arXiv preprint arXiv:1709.06212 (2017).
2-4 모든건 Deep Learning 으로.. (2018)
- Belghazi, Mohamed Ishmael, et al. "Mine: mutual information neural estimation." arXiv preprint arXiv:1801.04062 (2018).
- 이 연구는 ICML 2018에서 발표 되었다.
- 아래와 같은 생각에서 출발한 것 같다.
- "시대가 어느 때인데.. 아직도 어렵게 hyper-cube 어쩌구.. 디감마 어쩌구.. 측도론.. 이런거 하고 있니??"
- 그냥 예측하면 되는거 아닌가? 학습데이터 왕창 만들어서 딥러닝에 때려 넣어.. 딥러닝이 짱인데 왜 어렵게 그러고 있어..?
- probability distribtion과 그로부터 샘플링한 데이터와 mutual information을 엄청 많이 준비해두고 모델이 이를 그냥 학습하게 한 것이다.
3. 결론
- Mutual information 잘 예측하면 피어슨 상관계수보다 좋아요
- Mutual information 잘 예측해보려고 KSG를 시작으로 이것을 계량시킨 여러 방법들 있었어요
- KSG 너무 이론적으로 어려워요. 그냥 deep learning에 데이터 때려박아서 예측하는 방법 나왔어요.
