CCW?🔄

Counter Clockwise 알고리즘으로, 반시계 방향을 의미한다.

이름이 이렇게 지어진 이유는 세 점의 관계성이 다음과 같이 반시계 방향, 시계 방향, 일직선으로 이루어져있기 때문이다.

1. 반시계 방향

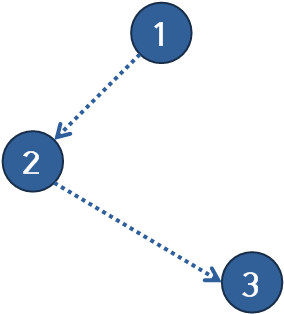
2. 시계 방향

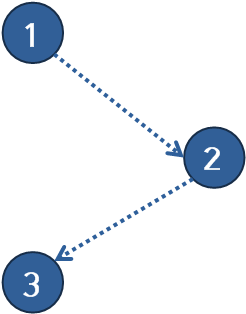
3. 일직선

(출처: https://jason9319.tistory.com/358)

방향을 알아보는 데는 다음의 공식이 존재한다.

사선 공식

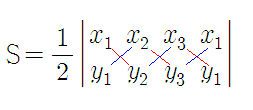
식의 형태때문에 신발끈 공식이라고도 불린다.

• 각각의 점을 A(x1, y1) , B(x2, y2), C(x3, y3) 의 좌표로 두고 함수에 넣어준다.

• 함수는 (x1y2 + x2y3 + x3y1) - (x2y1 + x3y2 + x1y3) 를 리턴한다.

리턴값이

• 음수이면 시계방향
• 양수이면 반시계방향
• 0이면 일직선

을 의미한다.

선분 교차 판별

위에서 알아본 알고리즘을 통해서 선분이 교차하는지 판별할 수 있다.

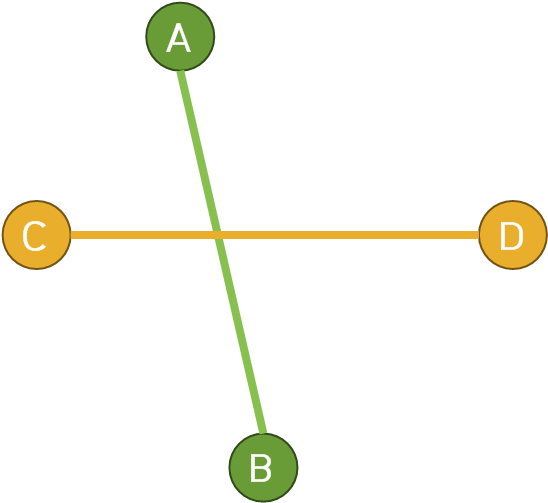
위 그림에서는 A-B를 기준으로 C와 D가 각각 다른 방향에 위치해 있다.

즉, 함수를 두 번 실행했을 때 각기 다른 부호이거나 0이어야만 교차가 가능하다고 할 수 있다.

CCW(A,B,C)*CCW(A,B,D) <= 0

💡 곱이 음수임에도 교차하지 않는 경우

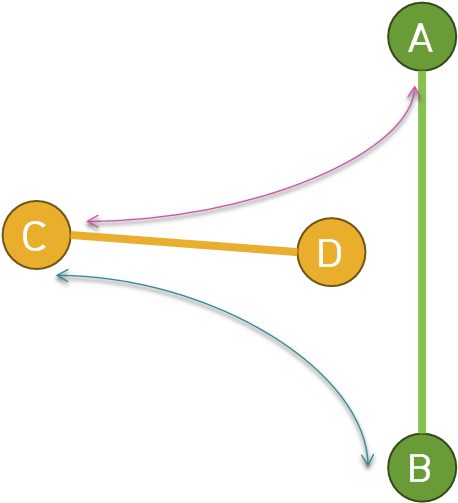
위 그림에서는 CCW(C,D,A)*CCW(C,D,B) <= 0이 성립하지만, 교차하고 있지 않다.

다음과 같은 경우를 위해서 CCW(A,B,C)*CCW(A,B,D) <= 0 인지도 알아보아야 한다.

즉, CCW(A,B,C)*CCW(A,B,D) <= 0 CCW(C,D,A)*CCW(C,D,B) <= 0 를 모두 알아본 후에, 최종적으로 선분 교차를 판단할 수 있게 된다.

💡 네 점이 일직선상에 있는 경우

마지막으로 고려해주어야 할 점은 네 점이 모두 한 직선 위에 있는 것으로,
CCW(A,B,C)*CCW(A,B,D) == 0 CCW(C,D,A)*CCW(C,D,B) == 0 인 경우이다.

이 경우에는 A,B와 C,D의 위치를 비교해서 교차하고 있는지 알아보아야 한다.

즉, 좌표가 큰 값이 서로의 작은 값보다 크다면 가능하다.

• A,B중 큰 좌표인 B가 C,D중 작은 좌표인 C보다 작기 때문에 교차 X

• A,B중 큰 좌표인 B가 C,D중 작은 좌표인 C보다 크기 때문에 교차 O

함수 코드

위의 예외사항까지 모두 고려한 함수 코드는 다음과 같다

# 신발끈 공식 함수
def sinbal(a,b,c):
    A = a[0]*b[1] + b[0]*c[1] + c[0]*a[1]
    B = a[1]*b[0] + b[1]*c[0] + c[1]*a[0]
    return A-B
# CCW 알고리즘 함수
def ccw(a,b):
    fx,fy,sx,sy = a[:2],a[2:],b[:2],b[2:]
    first = sinbal(fx,fy,sx)*sinbal(fx,fy,sy)
    second = sinbal(sx,sy,fx)*sinbal(sx,sy,fy)
    # 네 점이 일직선상에 있는 경우
    if first == 0 and second == 0:
    	# x에 더 작은 값이 오도록 함
        if fx > fy:
            fx,fy = fy,fx
        if sx > sy:
            sx,sy = sy,sx
        if fx <= sy and sx <= fy:
            return True
    
    else:
    	# 교차하는 경우
        if first <= 0 and second <= 0:
            return True
        else:
            return False