
트리의 순회
이전 글에서는 트리가 무엇인지, 그리고 이진 트리의 종류와 특징들에 대해서 알아보았다.
이번에는 트리 안에 있는 원소들을 순회하는 방식 3가지에 대해 알아보고자 한다.
트리는 리스트나 큐와 다르게, 반복문을 사용하는 것이 아닌 재귀적인 방식을 사용해야만 한다.
순회에는 3가지의 동작이 존재한다.
- 왼쪽 트리 부분을 끝까지 탐색한다.
- 오른쪽 트리 부분을 끝까지 탐색한다.
- 특정 노드를 탐색했다는 의미로 출력한다.
이 3가지의 동작의 선후관계에 따라서, 순회 방식은 전위 & 중위 & 후위 순회로 갈린다.
그럼 이제부터 3가지의 순회 방식과 python에서의 구현 코드를 알아보도록 하겠다.
tree는 구성된 이진 트리를 의미하고,root는 현재 노드를 의미한다.
전위 순회 (Pre-order)
Pre는 '~전에' 라는 뜻으로, 왼쪽과 오른쪽 트리 부분을 탐색하기 전에 현재 노드를 출력해준다는 의미이다.
그러므로 전위 순회는 다음과 같은 순서로 동작하게 된다.
① 특정 노드를 탐색했다는 의미로 출력한다.
② 왼쪽 트리 부분을 끝까지 탐색한다.
③ 오른쪽 트리 부분을 끝까지 탐색한다.
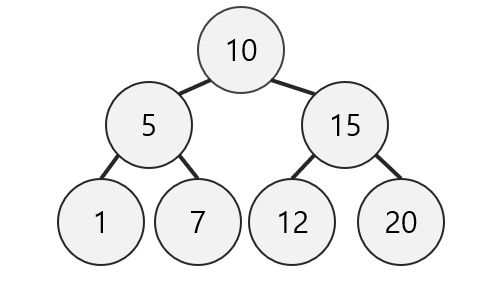
(출처: https://gowoonsori.site/data-structure/tree/)
위 그림을 통해서 알아보자.
-
출력이 우선이기에 루트 노드인
10이 출력된다. -
왼쪽 자식 노드로 이동한 후, 해당 노드인
5를 출력한다. -
다시 왼쪽 자식 노드로 이동, 해당 노드인
1을 출력한다. -
더 이상 갈 곳이 없기에, 부모 노드인
5로 돌아온 후 오른쪽 자식 노드로 이동하여7을 출력한다. -
이러한 과정을 반복하면
10 5 1 7 15 12 20순으로 출력이 된다.
이를 코드로 나타내면 아래와 같다.
# 전위 순회
def pre_order(root):
print(root, end = '') # root
pre_order(tree[root][0]) # left_child
pre_order(tree[root][1]) # right_child 중위 순회 (In-order)
중위 순회는 왼쪽 노드의 탐색을 먼저 진행하고, 현재 노드를 출력한 후에 오른쪽 노드의 탐색을 진행한다.
이쯤되면 감이 올텐데, 순회의 방식을 결정하는 것은 '언제 특정 노드를 출력 (방문처리) 해주는 것인가' 이다.
그러므로 중위 순회는 다음과 같은 순서로 동작하게 된다.
① 왼쪽 트리 부분을 끝까지 탐색한다.
② 특정 노드를 탐색했다는 의미로 출력한다.
③ 오른쪽 트리 부분을 끝까지 탐색한다.

그림을 통해서 알아보자.
-
왼쪽 자식 노드로만 끝까지 이동을 한 후에, 해당 노드인
1을 출력한다. -
부모 노드인
5에서의 왼쪽 트리 탐색을 마쳤기에, 본인인5를 출력한다. -
다음으로 오른쪽 자식 노드인
7을 출력한다. -
부모 노드인
10에서의 왼쪽 트리 탐색을 마쳤기에, 본인인10을 출력하고 오른쪽 트리 탐색을 진행한다. -
이를 반복하게 되면 최종적인 출력 순서는
1 5 7 10 12 15 20이 된다.
코드로 구현하면 다음과 같다. 출력해주는 코드의 순서만 가운데로 옮겨주면 된다.
# 중위 순회
def in_order(root):
in_order(tree[root][0]) # left_child
print(root, end = '') # root
in_order(tree[root][1]) # right_child후위 순회 (Post-order)
post는 '~후에` 라는 뜻으로 왼쪽과 오른쪽 트리의 탐색을 마친 후에 현재 노드를 출력해주는 방식을 말한다.
그러므로 후위 순회는 다음과 같은 순서로 동작하게 된다.
① 왼쪽 트리 부분을 끝까지 탐색한다.
② 오른쪽 트리 부분을 끝까지 탐색한다.
③ 특정 노드를 탐색했다는 의미로 출력한다.

그림을 통해서 알아보자.
-
왼쪽 트리의 끝인
1까지 이동한 후에 출력한다. -
부모 노드인
5로 다시 올라간 후에, 오른쪽 자식 노드인7로 이동한 후 출력한다. -
5에서의 왼쪽과 오른쪽 트리 탐색을 마쳤기에 이를 출력한 후, 부모 노드인10으로 올라간다. -
위와 동일한 방식으로
12 -> 20 -> 15를 출력하고 최종적으로 루트 노드인10을 출력한다. -
출력순서는
1 7 5 12 20 15 10이 된다.
이를 코드로 나타내면 아래와 같다.
# 후위 순회
def post_order(root):
post_order(tree[root][0]) # left_child
post_order(tree[root][1]) # right_child
print(root, end = '') # root(참고한 블로그: https://seongonion.tistory.com/41)
