[Python] G4_14938_서강그라운드 ⚔

https://www.acmicpc.net/problem/14938

문제

예은이는 요즘 가장 인기가 있는 게임 서강그라운드를 즐기고 있다. 서강그라운드는 여러 지역중 하나의 지역에 낙하산을 타고 낙하하여, 그 지역에 떨어져 있는 아이템들을 이용해 서바이벌을 하는 게임이다. 서강그라운드에서 1등을 하면 보상으로 치킨을 주는데, 예은이는 단 한번도 치킨을 먹을 수가 없었다. 자신이 치킨을 못 먹는 이유는 실력 때문이 아니라 아이템 운이 없어서라고 생각한 예은이는 낙하산에서 떨어질 때 각 지역에 아이템 들이 몇 개 있는지 알려주는 프로그램을 개발을 하였지만 어디로 낙하해야 자신의 수색 범위 내에서 가장 많은 아이템을 얻을 수 있는지 알 수 없었다.

각 지역은 일정한 길이 l (1 ≤ l ≤ 15)의 길로 다른 지역과 연결되어 있고 이 길은 양방향 통행이 가능하다. 예은이는 낙하한 지역을 중심으로 거리가 수색 범위 m (1 ≤ m ≤ 15) 이내의 모든 지역의 아이템을 습득 가능하다고 할 때, 예은이가 얻을 수 있는 아이템의 최대 개수를 알려주자.

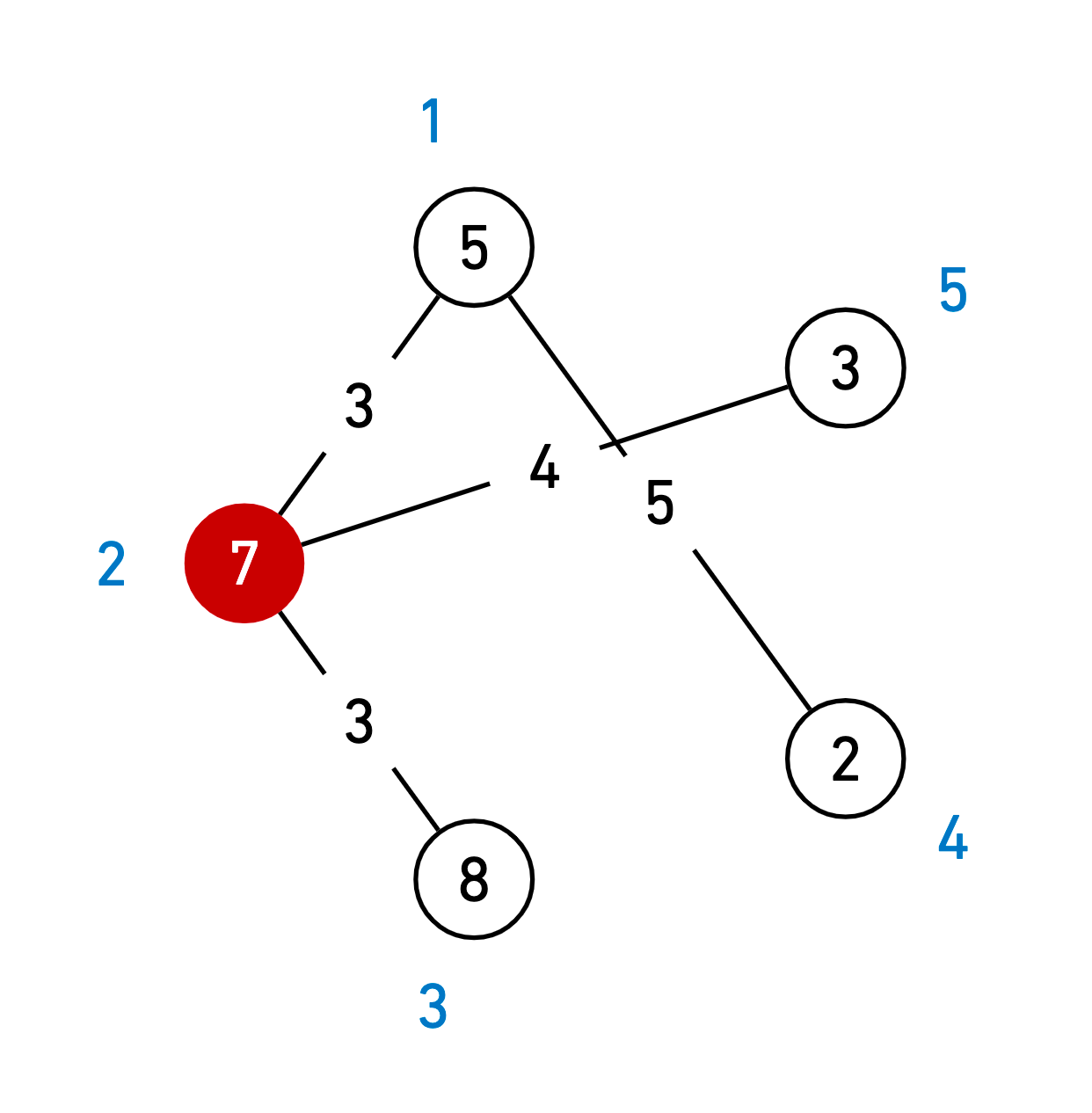
주어진 필드가 위의 그림과 같고, 예은이의 수색범위가 4라고 하자. ( 원 밖의 숫자는 지역 번호, 안의 숫자는 아이템 수, 선 위의 숫자는 거리를 의미한다) 예은이가 2번 지역에 떨어지게 되면 1번,2번(자기 지역), 3번, 5번 지역에 도달할 수 있다. (4번 지역의 경우 가는 거리가 3 + 5 = 8 > 4(수색범위) 이므로 4번 지역의 아이템을 얻을 수 없다.) 이렇게 되면 예은이는 23개의 아이템을 얻을 수 있고, 이는 위의 필드에서 예은이가 얻을 수 있는 아이템의 최대 개수이다.

입력

첫째 줄에는 지역의 개수 n (1 ≤ n ≤ 100)과 예은이의 수색범위 m (1 ≤ m ≤ 15), 길의 개수 r (1 ≤ r ≤ 100)이 주어진다.

둘째 줄에는 n개의 숫자가 차례대로 각 구역에 있는 아이템의 수 t (1 ≤ t ≤ 30)를 알려준다.

세 번째 줄부터 r+2번째 줄 까지 길 양 끝에 존재하는 지역의 번호 a, b, 그리고 길의 길이 l (1 ≤ l ≤ 15)가 주어진다.

지역의 번호는 1이상 n이하의 정수이다. 두 지역의 번호가 같은 경우는 없다.

출력

예은이가 얻을 수 있는 최대 아이템 개수를 출력한다.

예제

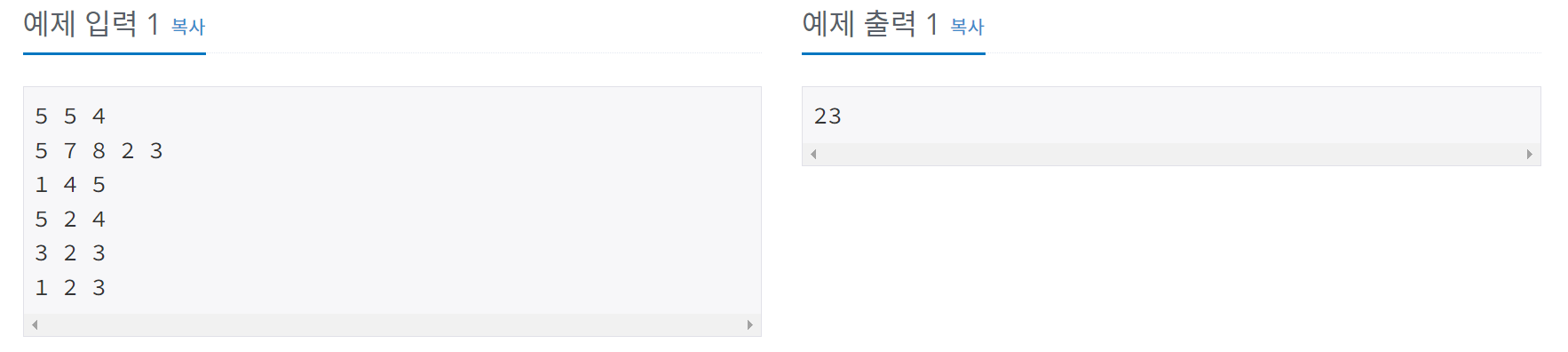
조건

• 시간 제한: 1초
• 메모리 제한: 128MB

코드

import sys
input = sys.stdin.readline
INF = sys.maxsize
# 입력
V,limit,E = map(int,input().split())    # 노드의 개수, 수색 범위, 간선의 개수
items = list(map(int,input().split()))  # 각 구역에 있는 아이템의 수
# 초기 그래프 설정
dp = [[INF]*V for _ in range(V)]
for i in range(V):
    dp[i][i] = 0 # 본인은 0
for _ in range(E):
    u,v,weight = map(int,input().split())
    # 양방향이므로
    if weight < dp[u-1][v-1]:
        dp[u-1][v-1] = weight
    if weight < dp[v-1][u-1]:
        dp[v-1][u-1] = weight
# 플로이드-워셜 알고리즘    
for k in range(V):
    for i in range(V):
        for j in range(V):
            if dp[i][j] > dp[i][k] + dp[k][j]:
                dp[i][j] = dp[i][k] + dp[k][j]
# 출력
result = 0                
for i in range(V):
    Sum = 0
    for j in range(V):
        # 수색 범위를 초과하는 경우
        if dp[i][j] > limit:
            continue
        Sum += items[j]
    result = max(result,Sum)
print(result)

이 문제는 플로이드-워셜 알고리즘을 통해서 각 노드별 간의 최단 거리를 구해준 다음에, 가능한 노드에 대해서만 아이템의 개수를 더해주면 되는 문제이다.

• 도달할 수 있는 거리의 한계점인 수색범위를 limit에 저장해준다.

• 각 노드별 도달 시 얻을 수 있는 아이템의 개수를 items에 저장해준다.

본인의 최단 거리는 0으로 설정한 후에, 입력받은 간선의 정보에 따라 초기 그래프를 설정한다.

• 양방향이기때문에, 시작 노드와 도착 노드의 위치를 바꾼 경우도 함께 저장해주어야 한다.

플로이드-워셜 알고리즘을 실행한다.

어느 지역에 처음으로 떨어져야 가장 많은 아이템을 얻을 수 있는지 구한 후, 출력한다.

• i는 처음으로 떨어지는 지역의 번호, j는 그 지역에서의 다른 노드들을 의미한다.

• 만약 i에서 j로 가는 거리가 수색 범위를 넘어선다면, 아이템을 얻을 수가 없다.

• if dp[i][j] > limit: continue

• result에는 떨어지는 지역들 중 가장 많이 얻은 아이템의 개수가 들어간다.

느낀 점 & 배운 점

1. 플로이드-워셜 알고리즘을 제대로 이해했다면 풀 수 있는 문제였다.

2. 양방향을 고려해주어야 하고, 수색범위에 따라 값을 더해주어야할지 말지를 정하는 것이 중요한 문제였다!