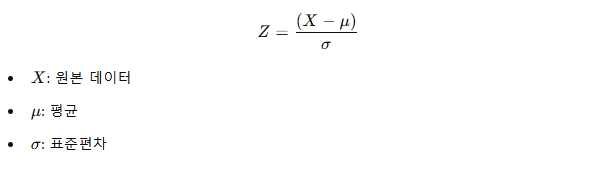z-표준화

표준화 (Standardization 또는 Z-score Normalization)

1. 정의

• 표준화는 데이터의 평균(mean)을 0으로, 표준편차(standard deviation)를 1로 변환하는 데이터 전처리 방법.
• Z-score 공식을 사용하여 계산:
  

---

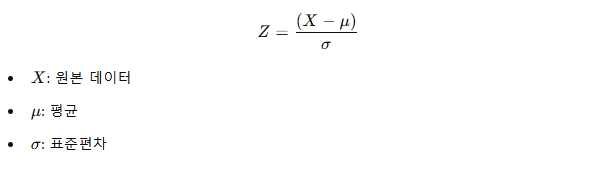
2. 목적

• 서로 다른 단위나 범위를 가진 데이터의 스케일을 동일하게 맞춤.
• 머신러닝 알고리즘(예: SVM, k-NN, PCA 등)이 데이터의 스케일에 민감하기 때문에 사용.
• 특징: 표준화 후에도 데이터의 분포 모양은 유지.

---

3. 예시

원본 데이터

• 키(cm): [150, 160, 170, 180]
• 몸무게(kg): [50, 65, 80, 90]

문제점

• 단위가 달라서 키와 몸무게를 직접 비교하거나 계산하기 어려움.
• 머신러닝 모델은 키(숫자가 큼)를 더 중요하게 여기게 될 수도 있음.

표준화 후

• 평균과 표준편차를 기준으로 값을 변환:
  • 키 → [ -1.34, -0.67, 0.67, 1.34 ]
  • 몸무게 → [ -1.72, -0.57, 0.86, 1.43 ]
• 결과적으로 값의 범위와 단위가 제거되고, 스케일이 같아짐.

---

4. Z-score와 데이터 분포

• 변환 후 데이터의 평균: 0
• 변환 후 데이터의 표준편차: 1
• 데이터의 상대적인 위치(값이 평균보다 크거나 작은 정도)가 유지됨.

---

5. 사용 예시 (Python 코드)

import numpy as np
from sklearn.preprocessing import StandardScaler

# 데이터 준비
data = np.array([[150, 50], [160, 65], [170, 80], [180, 90]])

# 표준화 수행
scaler = StandardScaler()
standardized_data = scaler.fit_transform(data)

print("원본 데이터:")
print(data)

print("\n표준화된 데이터:")
print(standardized_data)

---

6. 언제 사용하나?

• 데이터의 스케일(범위나 단위)가 서로 다른 경우.
• 선형 회귀, SVM, PCA, k-NN 등 거리 기반 알고리즘 사용 시.
• 주의: 트리 기반 알고리즘(예: 결정 트리, 랜덤 포레스트)은 표준화가 필요하지 않음.

---

7. 요약

• 표준화는 데이터의 스케일을 동일하게 만들어 모델 학습을 안정화.
• 평균을 0, 표준편차를 1로 변환.
• 데이터의 상대적 크기나 패턴을 유지하며 단위 차이를 제거.