Box-Cox, Yeo-Johnson Transformation

박스-콕스 변환 (Box-Cox Transformation)

1. 개념

박스-콕스(Box-Cox) 변환은 비대칭적이고 비정상적인 분포를 가진 데이터를 정규 분포에 가까운 형태로 변환하는 데 사용되는 방법이다.
이 방법은 데이터의 변환 파라미터인 람다를 찾는 방식으로 데이터를 변환한다.

박스-콕스 변환 공식:

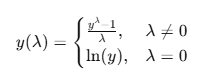
2. 사용 목적

• 비정상적인 분포를 가진 데이터를 정규 분포에 가깝게 변환하려고 할 때 사용한다.
• 많은 머신러닝 알고리즘은 정규 분포를 가정하기 때문에, 데이터를 정규화하는 것이 성능을 개선할 수 있음.
• 데이터의 왜도(skewness)를 조정하거나 평균-분산 불균형을 완화하려는 목적.

3. 람다 값에 따른 변화

• lambda = 1: 원본 데이터를 그대로 유지 (변환 없음)
• lambda = 0: 자연로그 변환 ((\ln(y)))
• lambda > 1: 데이터가 더 왼쪽으로 치우친 분포를 가진 경우
• lambda < 0: 데이터가 더 오른쪽으로 치우친 분포를 가진 경우

4. 예시

import numpy as np
from scipy import stats

# 예시 데이터 (왜도가 큰 데이터)
data = np.array([0.1, 0.5, 1.0, 2.0, 5.0, 10.0, 20.0])

# 박스-콕스 변환 (최적의 lambda를 찾음)
transformed_data, best_lambda = stats.boxcox(data)

print("박스-콕스 변환된 데이터:", transformed_data)
print("최적의 lambda 값:", best_lambda)

• 박스-콕스 변환을 통해 데이터가 더 정규 분포에 가까운 형태로 바뀌게 됨.

---

여-존슨 변환 (Yeo-Johnson Transformation)

1. 개념

여-존슨(Yeo-Johnson) 변환은 박스-콕스 변환을 음수 값을 처리할 수 있도록 확장한 방식.
즉, 박스-콕스 변환은 0 이하의 값에 대해 적용할 수 없지만, 여-존슨 변환은 음수 데이터를 포함한 데이터도 처리할 수 있음. 그래서 이게 sklearn.preprocessing에서 power_transform의 기본값임.

여-존슨 변환 공식:

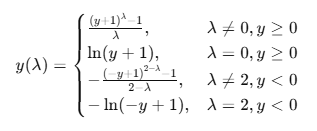
2. 사용 목적

• 박스-콕스 변환과 비슷하지만, 음수 값도 처리할 수 있다는 점에서 더 일반화된 변환 방법
• 박스-콕스 변환과 마찬가지로 데이터의 왜도(skewness)를 조정하여 정규 분포에 가깝게 만듦.
• 음수 값을 포함한 데이터에서도 적용할 수 있어, 더 넓은 범위의 데이터에 유용.

3. 예시

from scipy import stats

# 예시 데이터 (음수 값 포함)
data_with_negatives = np.array([0.1, -0.5, 1.0, 2.0, -5.0, 10.0, 20.0])

# 여-존슨 변환 (최적의 lambda를 찾음)
transformed_data, best_lambda = stats.yeojohnson(data_with_negatives)

print("여-존슨 변환된 데이터:", transformed_data)
print("최적의 lambda 값:", best_lambda)

• 여-존슨 변환을 통해 데이터가 정규 분포에 더 가까워지고, 음수 값을 처리할 수 있음.

---

박스-콕스와 여-존슨 변환의 차이점

• 박스-콕스: 음수 값을 처리할 수 없고, 양수 값에만 적용됨.
• 여-존슨: 음수 값도 처리할 수 있어, 더 다양한 데이터에 적용 가능.

결론

• 박스-콕스 변환은 데이터가 양수일 때 정규 분포를 만들기 위한 방법.
• 여-존슨 변환은 음수 값도 처리할 수 있도록 확장된 방법으로, 보다 일반적인 변환 방법.

코드적으로 봤을때 box-cox든 yeo-johnson이든 fit과 transform을 여타 sklearn 모듈처럼 나누지 않는다.
왜냐하면 box-cox와 yeo-johnson 모두 비교에 목적이 있는 것이 아니라, 단순히 데이터의 모양새를 정규표현식과 유사하게 변경시켜줌에 목적이 있기 때문이다.

그래서 보통 바로 아래와 같이 적용하게 된다.

from sklearn.preprocessing import power_transform
power_transform(data, method = ???)
# 여기서 기본적으로 method는 범용성이 좋은 yeo-johnson이다.