내삽과 외삽

본 글은
https://brunch.co.kr/@gimmesilver/1
위 페이지의 내용을 깊게 참고하여 학습 목적으로 정리한 글입니다.
많은 도움을 받고 있습니다.
깊은 감사를 전합니다.

1. 내삽과 외삽의 기본 개념

내삽(Interpolation)은 기존 데이터 범위 내에서 값을 예측하는 것이고, 외삽(Extrapolation)은 데이터 범위 밖의 값을 예측하는 것이다.
이를 게임 데이터로 설명하면 아래와 같다.

유저 수(만)	월 매출(억)
10	5
20	12
30	18
40	25

내삽 예시: 유저 수가 25만 명일 때의 매출을 예측하는 것
외삽 예시: 유저 수가 50만 명일 때의 매출을 예측하는 것

2. 네트워크 효과와 예측의 어려움

온라인 게임에서는 네트워크 효과로 인해 예측이 더욱 복잡해진다. 네트워크 효과란 사용자가 많아질수록 서비스의 가치가 높아지는 현상으로 다음과 같은 구조를 보인다.

1. 양의 피드백 메커니즘: 사용자 증가 → 서비스 가치 상승 → 추가 사용자 유입
2. 선순환 구조: 구독자 증가 → 콘텐츠 다양화 → 추가 구독자 확보

3. 예측 모델의 태생적 제약

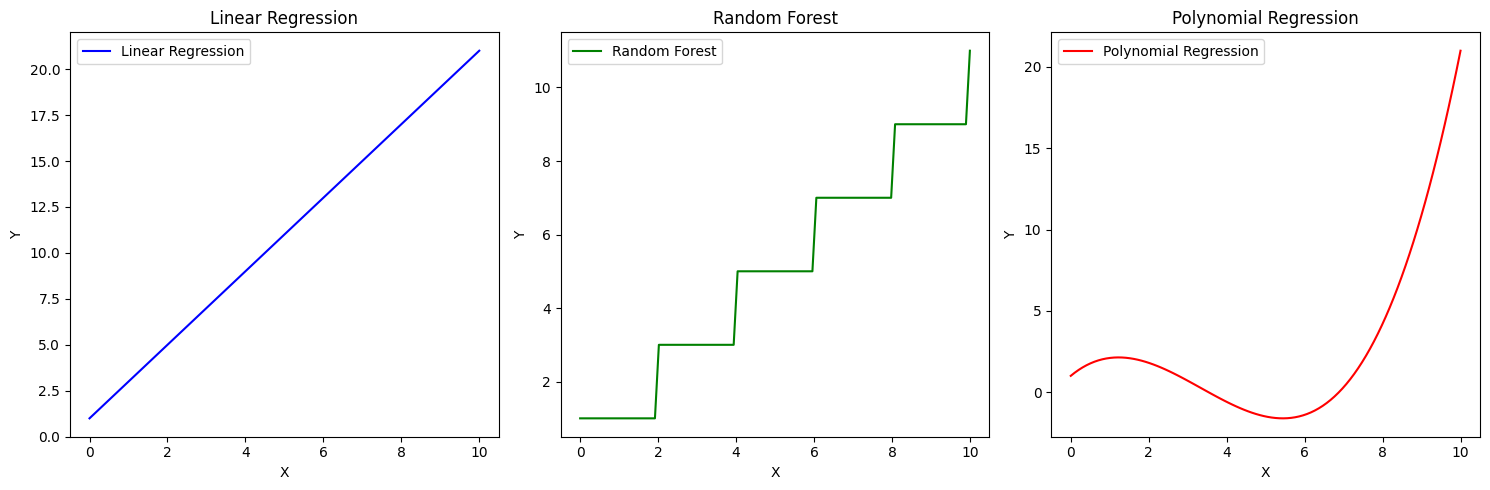
각 모델은 다음과 같은 특성을 가진다.

• 선형 회귀: 기울기가 항상 일정

  • 선형 회귀는 직선 형태로 데이터를 표현하기에, 애초에 기울기 자체가 일정하다.

• 랜덤 포레스트: 데이터가 없는 영역에서는 변화율이 0

  • 랜덤 포레스트는 여러 개의 의사결정 트리를 결합한 모델이다. 그래프에서 초록색 선을 보면, 계단 형태로 되어있는데, 이는 각 구간에서 예측값이 일정하게 유지되는 것을 의미한다.
    특히, 학습 데이터의 범위를 벗어난 영역에서는 마지막 값을 그대로 유지하므로 변화율이 0이 된다.

    이게 무슨 말인고,,,하면 아래와 같다.
    랜덤 포레스트의 특성을 구체적인 예시로 설명하겠습니다.

    다음과 같은 학습 데이터가 있다고 가정해보면

    X (입력값)	Y (출력값)
    2	1
    4	3
    6	5
    8	7
    10	9

    앞선 그래프의 초록색 선을 보면, X=10까지가 학습 데이터의 범위이고, 이 범위 내에서는 계단 형태로 예측이 이루어진다.

    만약 X=11, 12, 13... 등 학습 데이터 범위(X=10)를 벗어난 값을 예측하려고 한다면?

    • Y값은 계속 9에 머물게 된다.
    • 즉, X가 증가해도 Y는 변화하지 않음 (변화율 = 0)

    이는 랜덤 포레스트가 학습 데이터의 범위를 벗어난 영역에서는 가장 마지막에 학습한 값(이 경우 X=10일 때의 Y=9)을 그대로 사용하기 때문이다. 이것이 바로 "변화율이 0"이라는 의미!

    이러한 특성 때문에 랜덤 포레스트는 외삽(학습 범위 밖의 예측)에는 적합하지 않을 수 있다는 관점이 있다. (다변수에서도 마찬가지)

• 다항 회귀: 고차항으로 인한 과적합 위험

  • 다항 회귀의 경우에 곡선 형태로 데이터를 표현할 수 있으며, 앞선 그래프에서 빨간색을 보면 고차항으로 인해 곡선 형태를 띄는 것을 볼 수 있다.
    다만, 차수가 높아질 수록 학습 데이터에 과도하게 맞추려는 경향이 있어 과적합이 발생할 위험이 크며, 이는 그래프에서 급격한 곡선의 변화로 나타나게 된다.

4. 실무 적용점

4.1 내삽이 효과적인 분석 작업

유저 행동 분석

• 레벨별 플레이타임과 결제율 관계 분석
• 특정 레벨 구간의 이탈률 예측
• 게임 난이도 조절을 위한 구간별 클리어 시간 분석

수익화 모델 최적화

• 아이템 가격 책정을 위한 구매 확률 추정
• 레벨별 인앱 결제 패턴 분석
• 유저 세그먼트별 구매력 예측

4.2 외삽 적용 시 주의가 필요한 영역

신규 시장 예측

• 새로운 지역 출시 시 예상 매출 추정
• 신규 플랫폼 진출 시 유저 유입량 예측
• 새로운 장르로의 확장 시 시장 규모 추정

장기 성과 예측

• 게임 수명주기 예측
• 장기 매출 추정
• 서버 확장 계획 수립

4.3 정확도 향상을 위한 전략

데이터 보강

• 유사 장르 게임들의 성과 데이터 수집
• 경쟁사 사례 분석을 통한 벤치마킹
• 시장 환경 변수를 고려한 보정

하이브리드 접근

• 내삽과 외삽을 결합한 단계적 예측 모델 구축
• 단기 예측은 내삽, 장기 예측은 보정된 외삽 활용
• 실시간 데이터로 지속적인 모델 업데이트