
상관관계분석
- 상관관계(Correlation)란?
상관관계는 두 개 이상의 "수치형 변수"가 서로 어떤 관계를 가지고 있는지, 그리고 그 관계의 "강도"와 "방향성"이 어떤지를 나타내는 통계적 척도
즉, "하나의 수치형 변수가 커질 때, 다른 수치형 변수도 함께 커지는지 혹은 작아지는지" 같은 "수치형-수치형 관계"를 파악할 때 사용
- 상관관계 유형
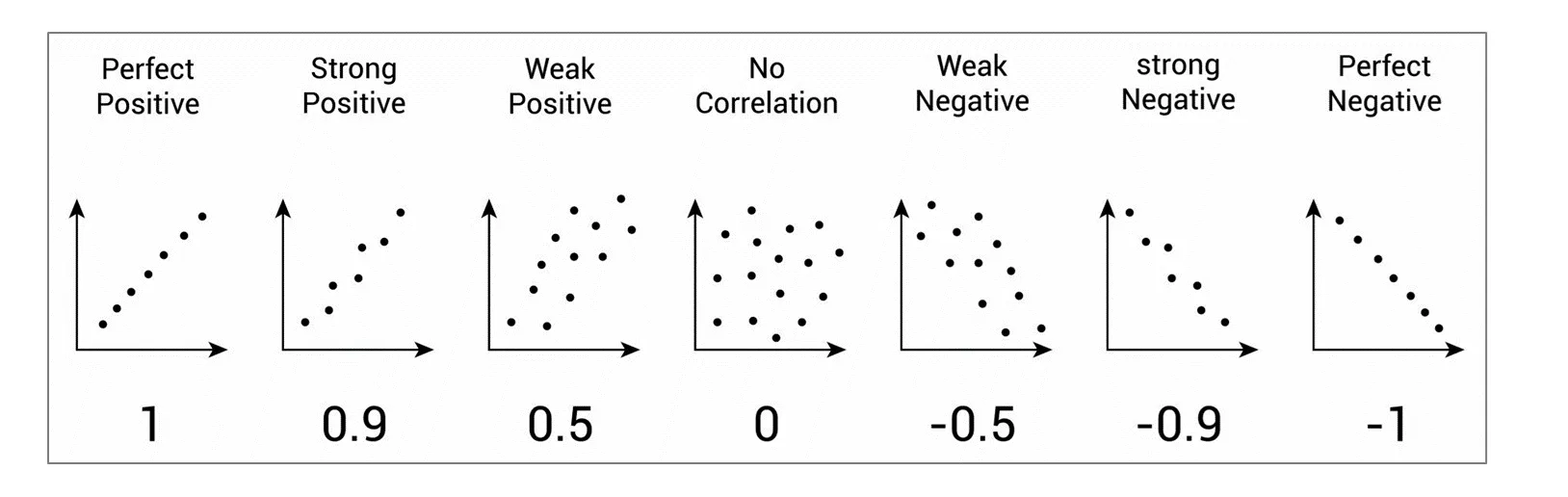
➡️ 양의 상관관계(Positive Correlation): 한 변수의 값이 증가할 때 다른 변수의 값도 함께 증가하는 경향을 보이는 관계
(예: 광고비와 매출액)
➡️ 음의 상관관계 (Negative Correlation): 한 변수의 값이 증가할 때 다른 변수의 값은 감소하는 경향을 보이는 관계
(예: 상품 가격과 판매량)
➡️ 무상관 (No Correlation): 두 변수 사이에 일정한 선형적인 관계가 없는 경우
(예: 고객의 거주 지역과 구매하는 상품의 색상)
- 상관계수(Correlation Coefficient)의 이해
두 변수 간의 선형적 관계의 강도와 방향을 수치로 나타낸 값
여러 종류의 상관계수가 있지만, 가장 일반적으로 사용되는 것은 피어슨(Pearson) 상관계수
피어슨 상관계수
- 두 변수가 연속형(Continuous)이고, 두 변수 간의 관계가 선형(Linear)이라는 가정을 전제
- 값의 범위: −1에서 +1까지의 값
- r=+1: 완벽한 양의 선형 상관관계 (점들이 우상향 직선에 놓임)
- r=−1: 완벽한 음의 선형 상관관계 (점들이 우하향 직선에 놓임)
- r=0: 선형적인 관계가 없음 (무상관에 가까움)
- 상관계수의 강도 해석 (일반적인 가이드라인, 절대적 기준 아님):
- ∣r∣≥0.7: 매우 강한 상관관계
- 0.5≤∣r∣<0.7: 강한 상관관계
- 0.3≤∣r∣<0.5: 보통의 상관관계
- 0.1≤∣r∣<0.3: 약한 상관관계
- ∣r∣<0.1: 거의 상관관계 없음
스피어만 상관계수
- 데이터가 순서형(Ordinal)이거나, 이상치가 많거나, 관계가 비선형적일 때
- 수치 값 의미보다 순서가 중요한 경우
- 설문조사에서 사람들의 "만족도(1~5등급)" vs "재구매 의도(1~5등급)"
- 이상치가 많은 경우
- 수입과 행복도 조사에 몇몇 억만장자가 있는 경우
- 관계가 직선형이 아닌 경우
- 운동 시간 증가 vs 행복감
- 수치 값 의미보다 순서가 중요한 경우
- 원래의 데이터를 순위(Rank)로 변환하여 피어슨 상관계수와 동일한 방식으로 계산
상관관계 분석의 활용 및 과정
-
상관관계 분석의 목적
- 두 변수 간에 통계적으로 유의미한 선형적 관계가 존재하는 검정
- 그 관계의 방향(양의/음의)과 강도(얼마나 강하게 관련되어 있는지)를 파악
- 데이터 간의 숨겨진 패턴이나 상호작용을 탐색하여 인사이트 도출분석 과정
- 가설 설정:
- 귀무가설 (H0): 두 변수 간에는 선형적 상관관계가 없다 (상관계수 ρ = 0).
- 대립가설 (H1): 두 변수 간에는 선형적 상관관계가 있다 (상관계수 ρ != 0).
- 데이터 준비: 분석할 변수들을 선택하고 결측치 처리, 이상치 확인 등 데이터 전처리 과정을 수행합니다.
- 산점도 확인: 먼저 시각적으로 변수 간의 관계 패턴을 확인하여 선형 관계 가정이 적절한지 판단합니다.
- 상관계수 계산: 피어슨 또는 스피어만 상관계수를 계산합니다.
- 가설 검정: 계산된 상관계수에 대한 유의확률(p-value)을 통해 귀무가설의 기각 여부를 결정합니다.
- 일반적으로 p<0.05 이면 귀무가설을 기각하고, "두 변수 간에는 통계적으로 유의미한 상관관계가 있다"고 결론 내립니다.
- 결과 해석: 상관계수의 값과 p-value를 종합하여 관계의 방향, 강도, 유의미성을 설명합니다.
- 가설 설정:
카이제곱 검정
카이제곱 검정(Chi-squared Test)이란?
카이제곱 검정은 두 개의 "범주형 변수" 간의 관련성(독립성 검정) 또는 "관측된 범주형 데이터 빈도 분포가 기대되는 빈도 분포와 유의미하게 다른지" (적합도 검정)을 확인할 때 사용
즉, "범주형 변수 간의 연관성 여부"를 검정하는 방법"**
독립성 검정
두 범주형 변수들이 서로 독립인지(= 관련성이 없는지) 또는 서로 관련성이 있는지 확인
Q: 성별에 따라 결제 여부 차이가 있는가?
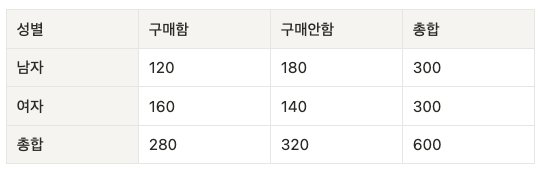
A: 결과 해석:
- p-value < 0.05 이면 → 귀무가설 기각
- 성별과 구매 여부는 독립이 아니다(= 관계가 있다)
- p-value ≥ 0.05 이면 → 귀무가설 유지
- 성별과 구매 여부는 독립적이다
[사용 예시]
1. 마케팅 캠페인 효과 분석
2. 고객 행동 패턴 분석
3. UI/UX 개선 효과 분석
카이제곱 분포의 특징
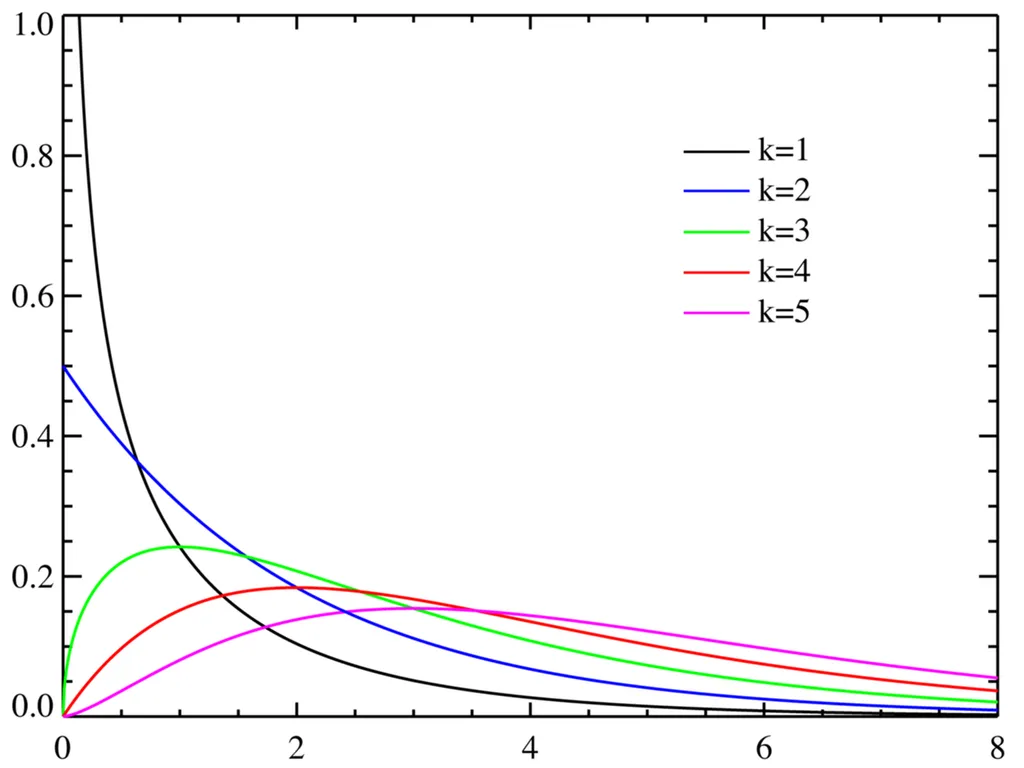
- 음수 값을 갖지 않음: 카이제곱값은 항상 0 이상의 값을 가짐
- 비대칭적 분포: 분포가 0에서 시작해서 양의 방향으로 길게 꼬리를 뻗는 비대칭적인 형태, 하지만! 자유도가 커질수록(≒ 데이터 수가 많아질수록) 분포의 봉우리가 오른쪽으로 이동하고 정규 분포 형태에 가까워짐
- 카이제곱 검정 시 왜 카이제곱 분포를 따르는가? 카이제곱 검정 통계량이 카이제곱 분포를 따른다고 수학적으로 증명되었기 때문
t-검정
t-검정이란?
t-검정은 "두 집단 간의 평균 차이"를 검정할 때 사용되는 통계적 방법
여기서 말하는 두 집단은 주로 "범주형 변수(집단 구분)"에 의해 나뉘며, 각 집단의 대상이 가지는 "수치형 변수(측정값)"의 평균을 비교
즉, "범주형 변수와 수치형 변수 간의 관계"를 검정할 때 사용**
언제 쓸까요??
- 모집단의 분산(표준편차)을 알지 못하거나
- 표본의 크기가 비교적 작을 때
독립 표본 t-검정 (Independent Samples t-test)
서로 독립적인 두 집단의 평균이 통계적으로 유의미한 차이가 있는지 검정
[사용 예시]
- "새로운 웹사이트 레이아웃(A안)과 기존 레이아웃(B안)이 고객의 평균 구매액이 다른가?"
- "두 가지 다른 할인 쿠폰 전략(5% 할인 vs. 1000원 할인)이 고객의 평균 장바구니 가치에 차이를 보이는가?”
- "무료 체험 플랜을 이용하는 고객과 유료 월간 구독 플랜을 이용하는 고객 간에 평균 앱 사용 시간에 차이가 있는가?"
대응 표본 t-검정 (Paired Samples t-test)
같은 집단(동일한 대상)에서 두 시점 또는 두 조건에서의 평균 차이가 통계적으로 유의미한지 검정
[사용 예시]
- "새로운 UI를 적용하기 전과 후, 동일 유저들의 평균 웹사이트 체류 시간에 유의미한 변화가 있는가?”
- "리타게팅 광고를 노출하기 전과 노출한 후 동일 고객들의 평균 주간 방문 횟수에 유의미한 변화가 있는가?"
- "상품 상세 페이지의 구매 버튼 위치를 변경하기 전과 후의 평균 구매 완료 시간에 차이가 있는가?" (동일 유저 대상)
스튜던트 t 분포(Student's t-distribution)의 이해
- 스튜던트 t 분포의 특징
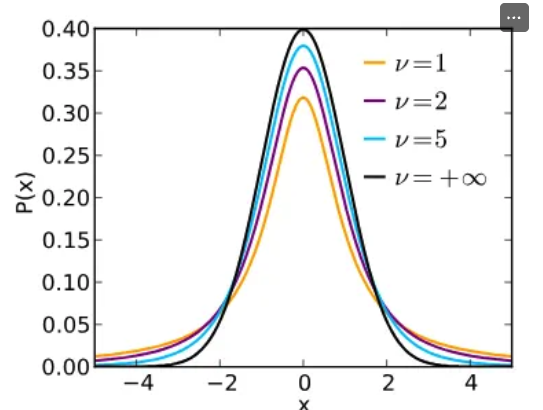
- 종 모양 및 대칭성: 정규 분포(Z 분포)와 유사하게 0을 중심으로 대칭인 종 모양을 가집니다.
- 꼬리 두께: 정규 분포에 비해 꼬리가 더 두껍습니다. 이는 표본의 크기가 작을 때 발생하는 불확실성(모집단 표준편차를 정확히 알 수 없기 때문에)을 반영하여, 극단값에 대한 확률을 더 높게 부여하기 위함입니다.
- 정규 분포로의 수렴: 자유도가 증가할수록 (즉, 표본 크기가 커질수록) t 분포는 점점 정규 분포와 비슷해지며, df≥30 정도가 되면 거의 정규 분포와 구별하기 어렵게 됩니다.
오늘의 인사이트
어..? 인사이트라고 할 만한게 없는데 일단 속이 좋지 않다.
그것보다는 내가 데이터 전처리, 시각화해서 가설 검증을 했다고 생각했을 때 어떤 방식을 사용해서 검증해야하는지 생각하는 것이 좋겠다.
