신경망 개요

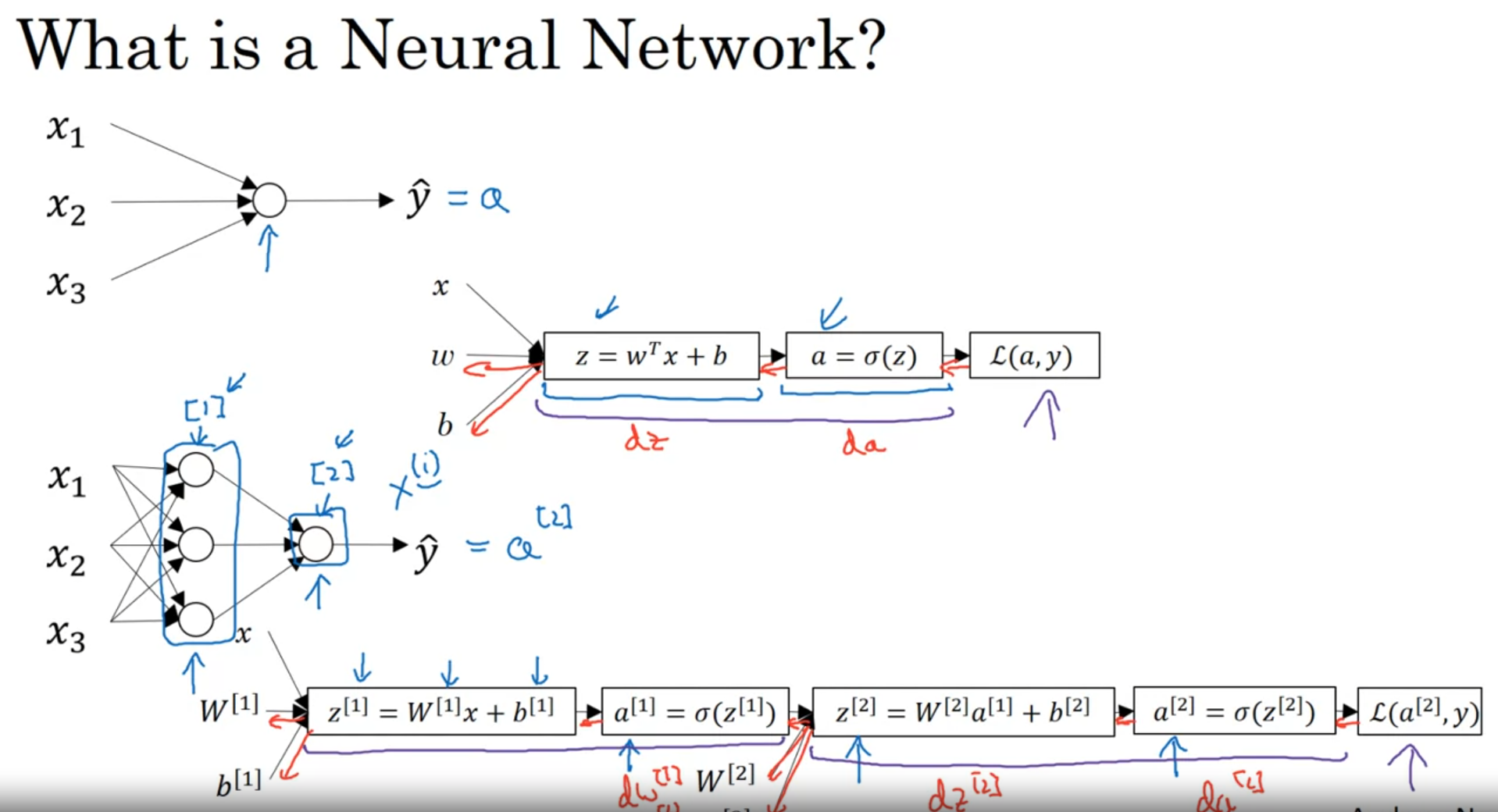
레이어를 [1], [2]... 으로 표현

$x_1$ $x_2$ $x_3$ 특성을 표현

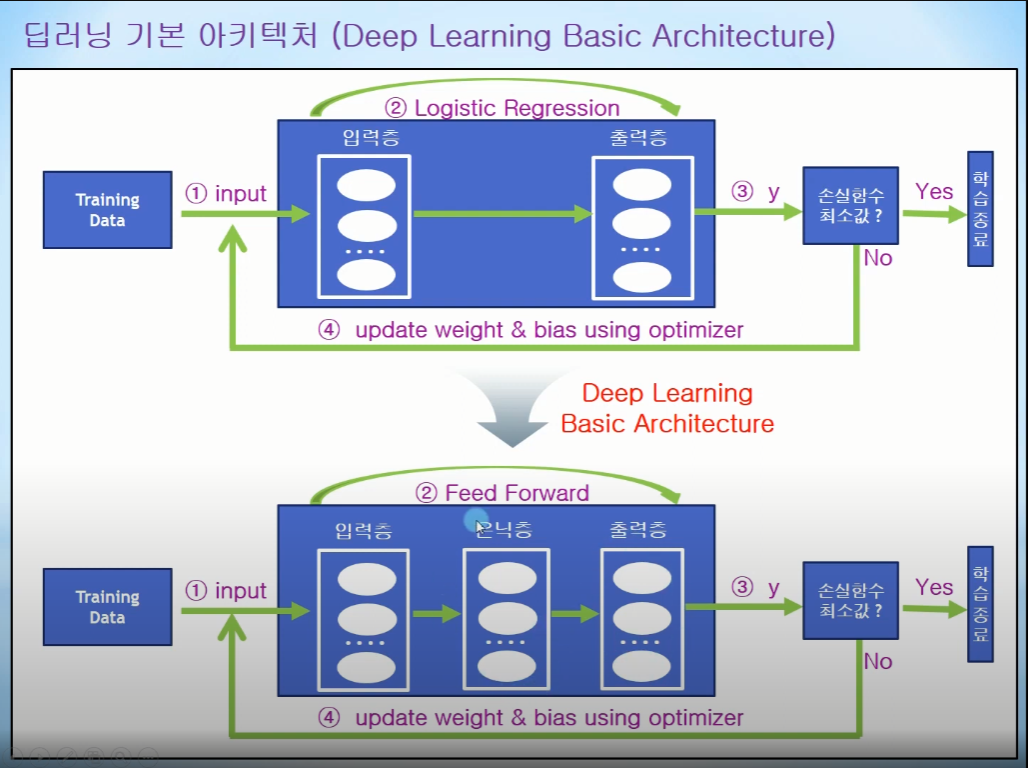
개인적으로 NeoWizard 채널이 한국어라서 그런지 이해가 더 쉽....다 ㅜㅜ

신경망 표현

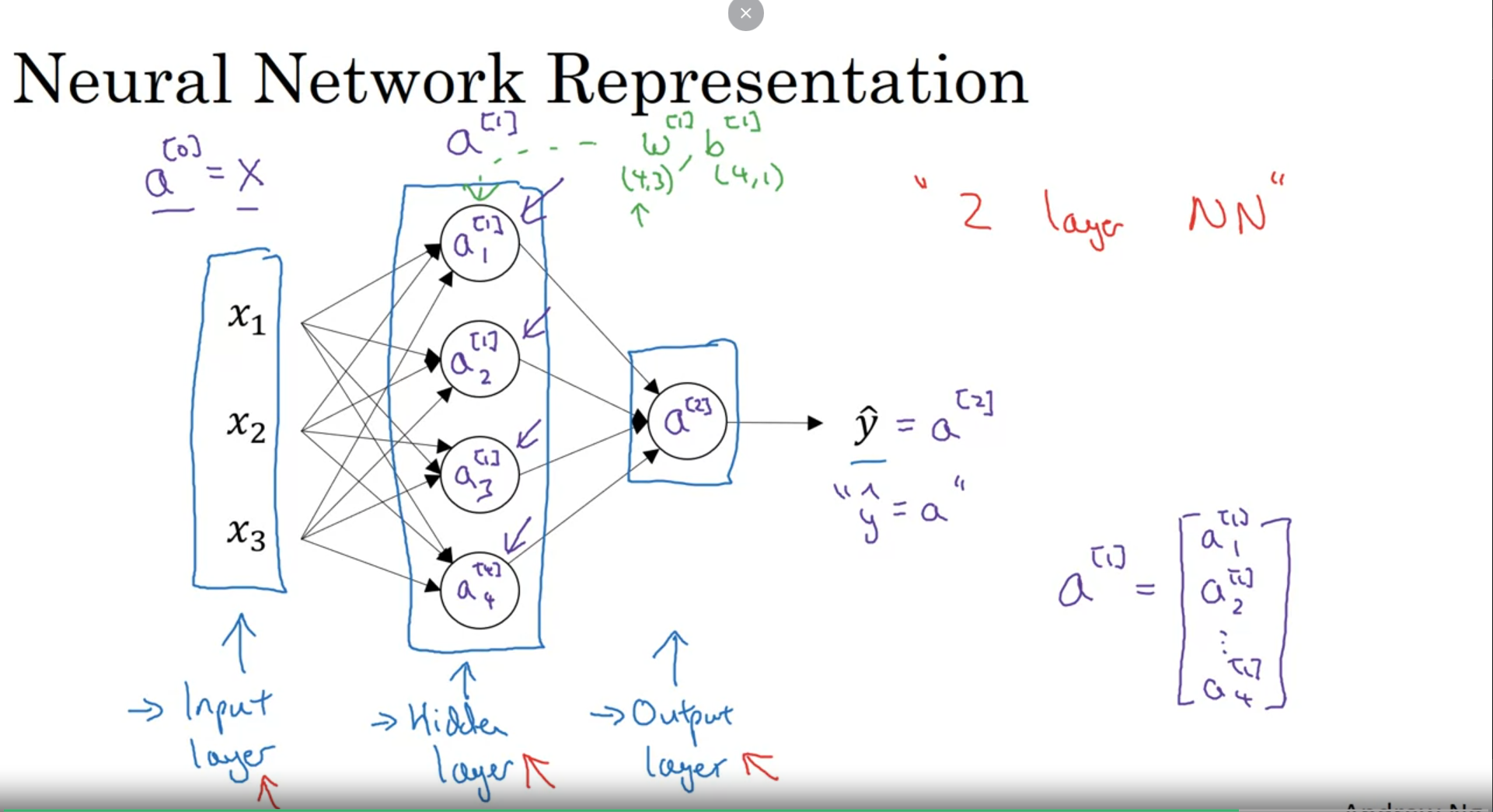
개요에서 설명했던 표현법들을 보여줌!!!

신경망의 출력 계산하기

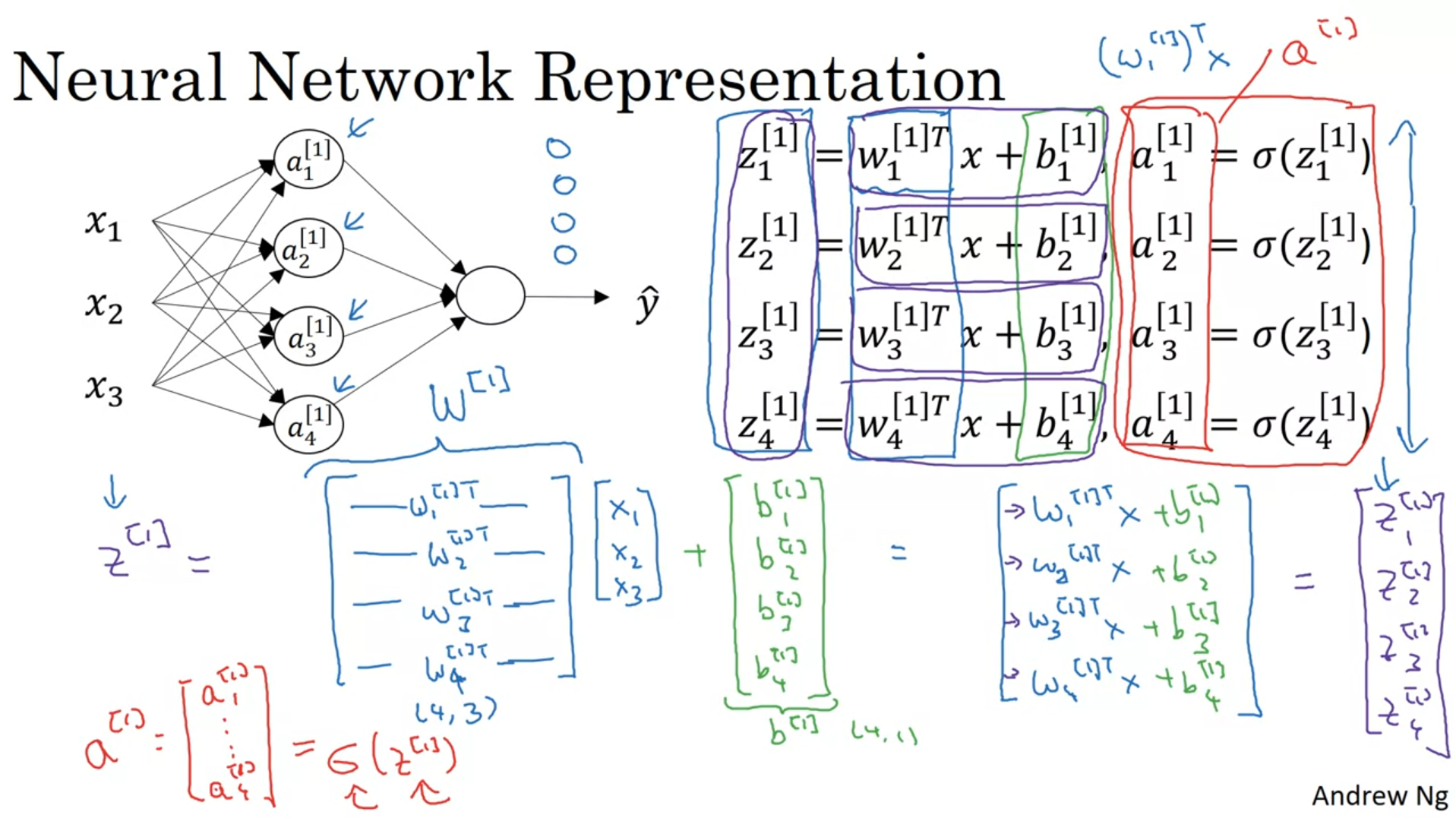
신경망을 벡터화해서 표현

$W ^{[1]}$ => 4($a^{[1]}$층의 개수)x3(특성$x_1$의 수) (4X3행렬)
b => 4($a^{[1]}$층의 개수)x1(편향 b는 1개이므로) (4X1행렬)

마지막 $a_1^{[1]}$ 시그모이드 !!!! $a_1^{[1]}$ = $\hat{y}$

설명하는 사람에 따라 문자는 바뀔 수 있다

여러 예제에서 벡터화하기

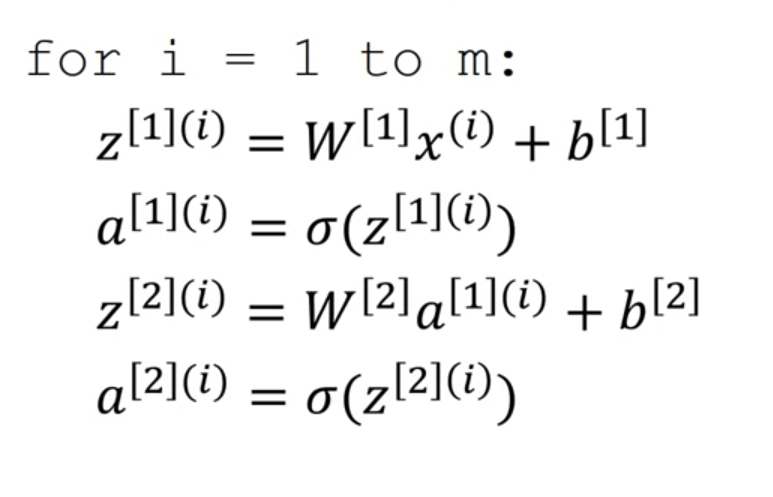
$a^{[2](i)}$ 에서 대괄호는 레이어 소괄호는 훈련예제

벡터화 하기전에 요소?로 표현하기 위해 저렇게 표기함
결국에 행렬 안으로 들어감

행렬은 $X^{[n]}$, $Z^{[n]}$, $A^{[n]}$ 으로 표기함

가로는 타겟샘플, 세로는 레이어 수를 표현!!!

벡터화 된 구현에 대한 설명

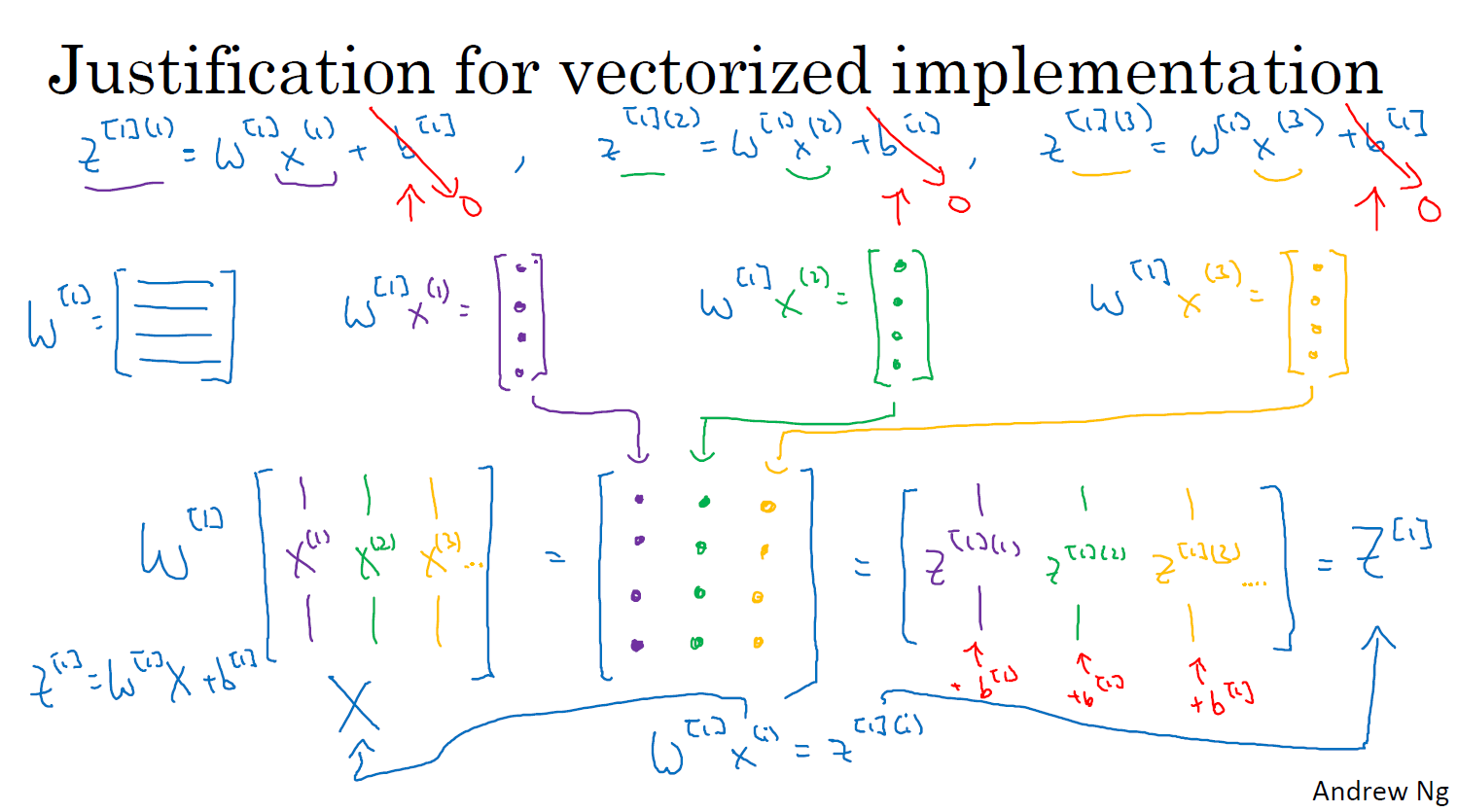
브로드캐스팅을 이용하게되면 아주 간결해진다!!

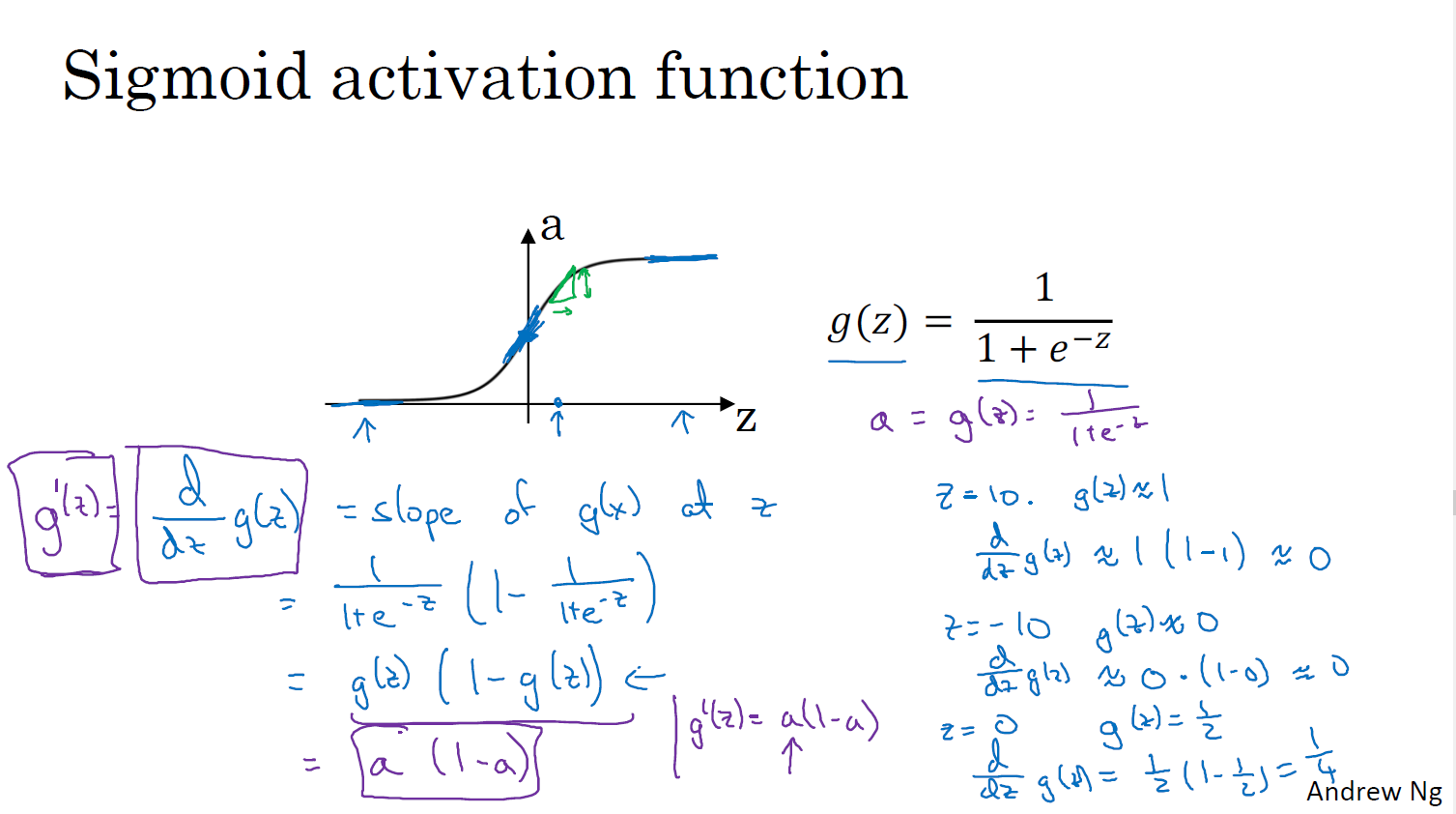
활성화 함수

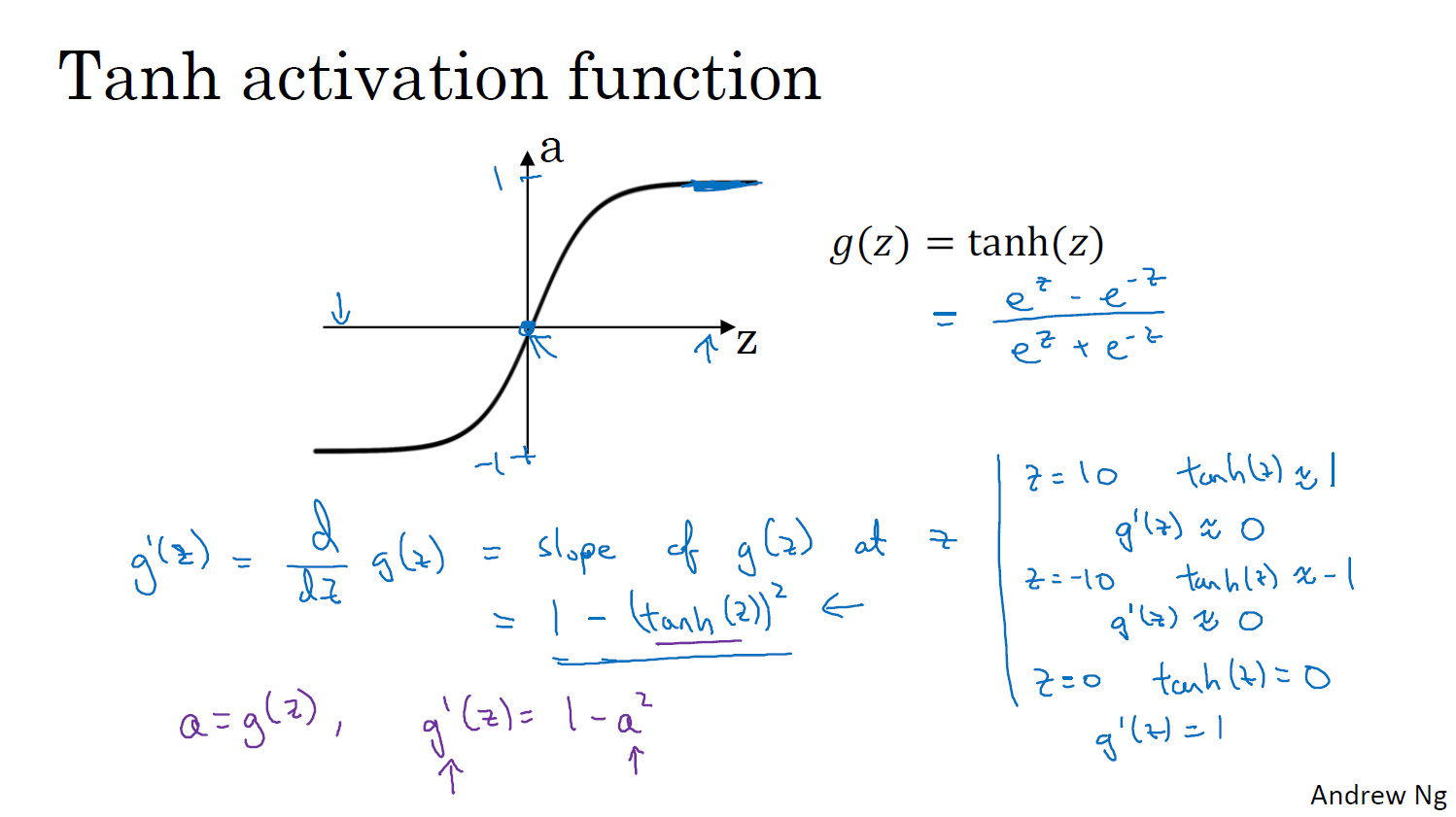
tanh가 활성화의 평균이 0이 되어 더 잘 작동한다고 함

0.5가 평균이 아니라 0에 가까워 데이터를 중심으로 하는 효과가 있다

시그모이드는 거의 안쓴다... tanh를 더 많이쓴다..

단점은 y=$z^{[1]}$가 매우 크거나 작으면 기울기가 0에 가까워 기울기 하강속도가 느려짐

비선형 활성화 함수가 필요한 이유는 무엇인가요?

• 선형함수를 사용하면 기울기가 변하지 않기 떄문
• 위 오른쪽 수학 공식으로도 표현했다

  회귀문제를 러닝머신할 때는 사용

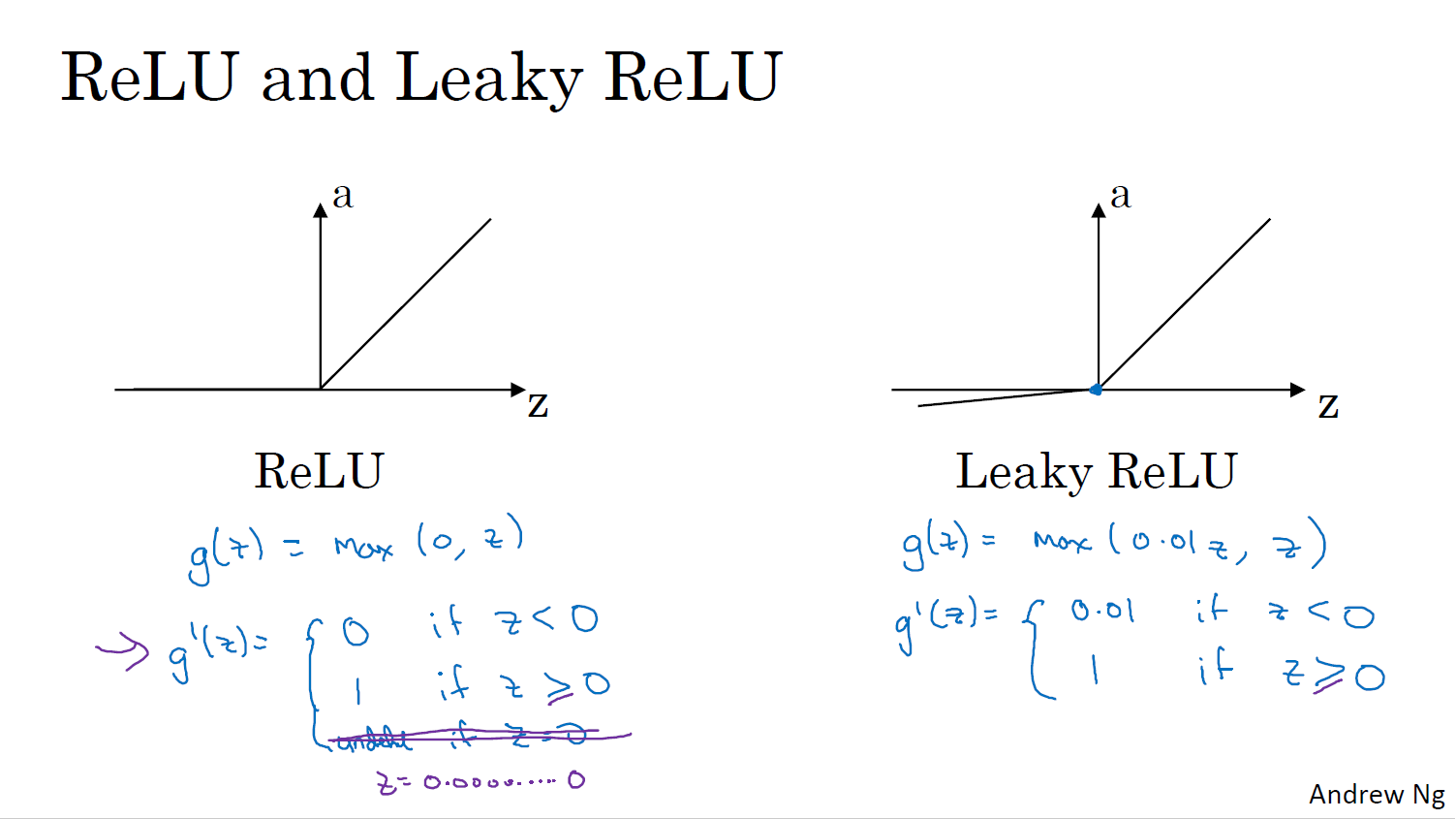
활성화 함수의 파생 함수

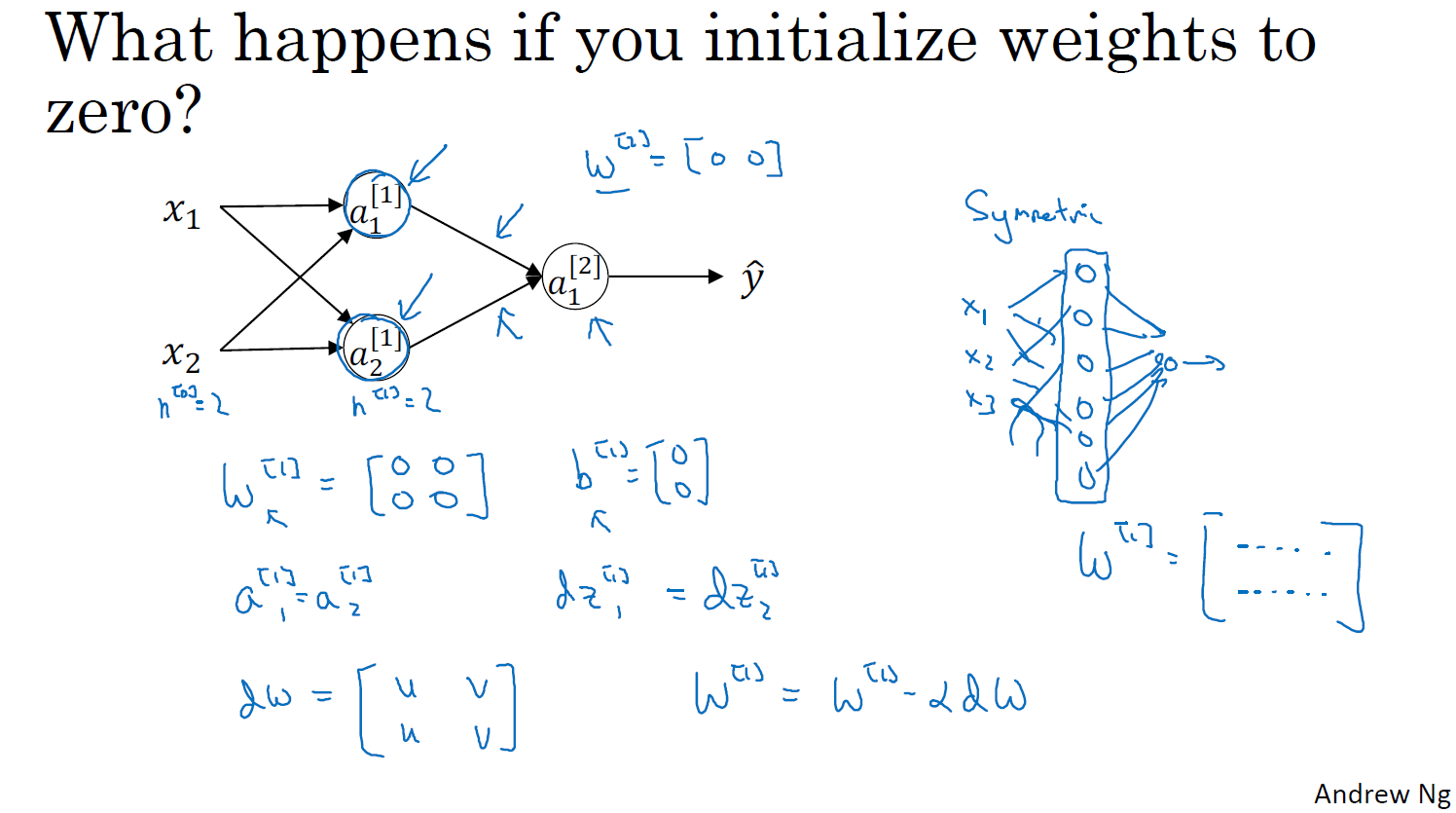
무작위 초기화

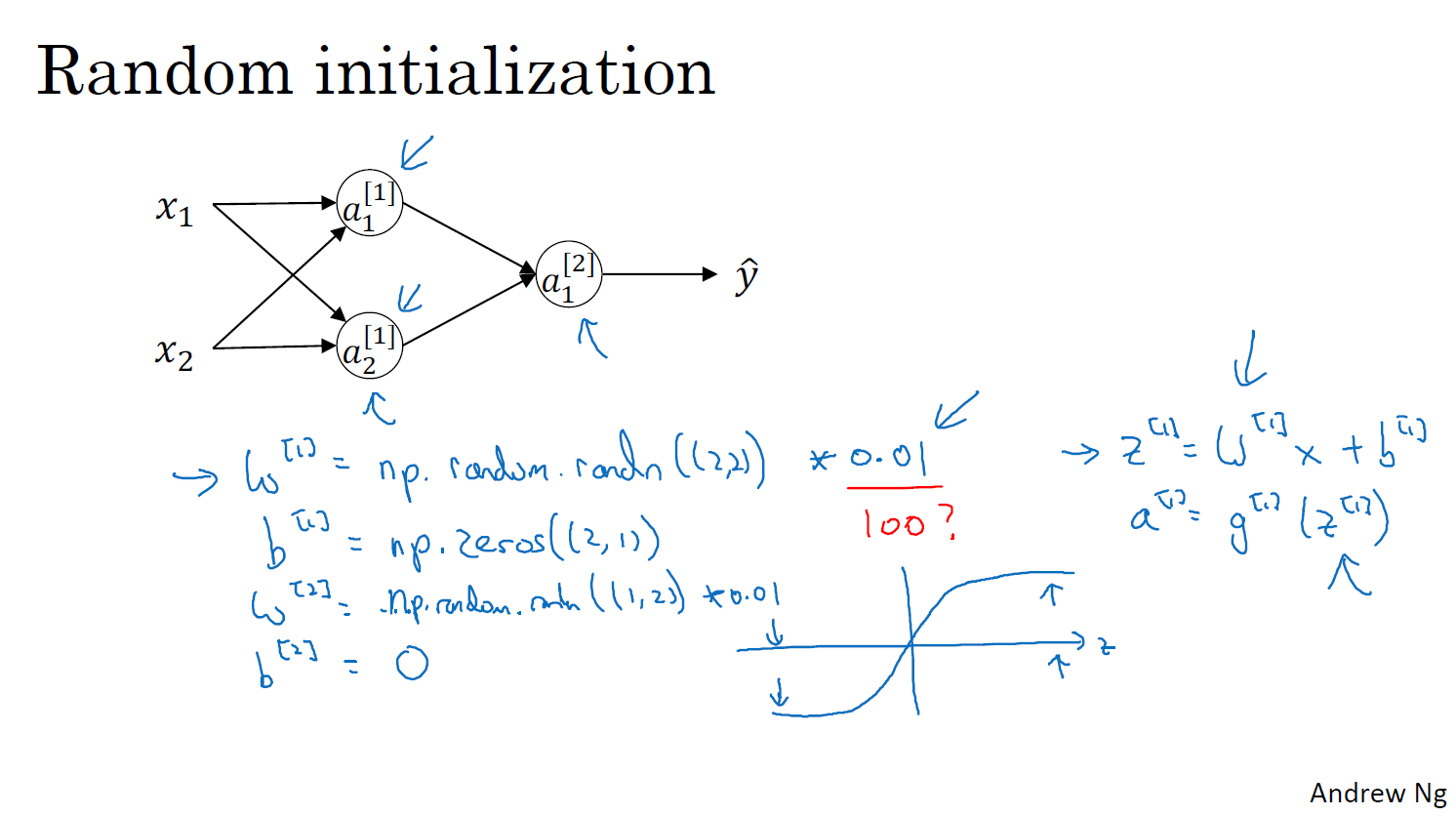
가중치는 크게 하면 안된다.

많은 활성화 함수(예: 시그모이드 함수, 탄젠트 함수)는 입력 값이 너무 크거나 작으면 출력이 포화 상태에 이릅니다. 예를 들어, 시그모이드 함수는 입력이 매우 크면 1에 가까워지고, 매우 작으면 0에 가까워집니다. 이러한 경우, 역전파 시 기울기가 매우 작아져(즉, 기울기 소실 문제) 학습이 거의 일어나지 않습니다

기울기 소실 ,기울기 폭발, 학습 불안정성

참고

https://strongai.tistory.com/29