[ ᴀʟɢᴏʀɪᴛʜᴍ ] Dynamic Programming ( 다이나믹 프로그래밍 )

NewHa·2023년 9월 18일

algorithm

ᴀʟɢᴏʀɪᴛʜᴍ

목록 보기

17/19

DP(Dynamic Programming)

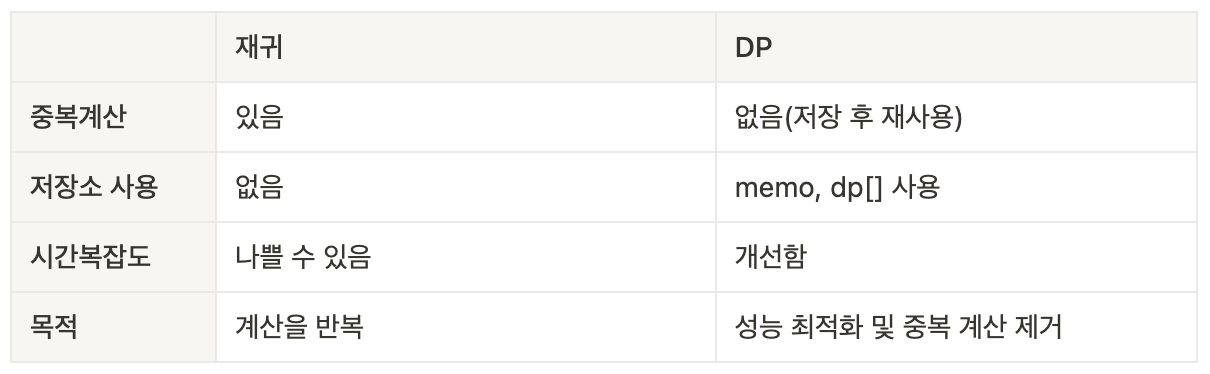
한 번 계산한 결과를 저장해두고, 다시 계산하지 않도록 하여 효율성을 높이는 알고리즘 기법입니다.

Dynamic Programming 의 의미

한국어로 하면 “동적 계획법” 혹은 “동적 프로그래밍”이라고 하는데, 그냥 봐서는 이게 무슨 뜻인지 이해가 잘 안 갔습니다.

여기서의 “Dynamic”이나 “Programming”이라는 단어가 흔히 쓰이는 뜻과는 조금 다르기 때문입니다.

우선, DP라는 이름은 1950년대 미국의 수학자 리처드 벨먼(Richard Bellman)이 지었습니다. 당시 그는 군사 최적화 문제를 연구하면서 국방부에서 싫어하는 단어(수학, 최적화, 계획 등)를 피해 정치적으로 중립적이고, 거부감 없는 이름을 일부러 만들었습니다. 이게 Dynamic Programming 입니다.

"Dynamic이라는 단어는 그럴싸하게 들리고, Programming은 어떤 계획 절차를 의미할 수 있어서 좋았다."
— 리처드 벨만

각 단어가 기존 의미인 ‘역동적인’, ‘프로그래밍’ 이라는 뜻이 아니라, ‘계산이 진행되면서 상태가 계속 바뀐다’와 ‘최적의 계획을 세우다’라는 의미를 가집니다. 즉, 계산이 진행되면서 바뀌는 상황에서, 최적의 전략이라는 의미를 가집니다.

이러한 최적의 전략이 바로, 계산했던 걸 저장해서 재사용하자입니다. 따라서 DP는 단지 코드, 알고리즘이 아닌 ‘어떻게 문제를 풀지에 대한 사고방식’으로 전략에 해당합니다.

DP가 필요한 이유

가장 흔하게 드는 예시가 “피보나치 수열”입니다. 피보나치 수열을 재귀로 풀면 다음과 같습니다.

🔗

재귀에 관해서는 다음 게시글을 참고해주세요.

function fibo(n) {
  if (n <= 2) return 1;
  return fibo(n - 1) + fibo(n - 2);
}

쉽게 작성했지만, 위 방식은 O(2ⁿ)의 시간복잡도를 가지고, 중복 계산이 아주 많습니다.

예를 들면, fibo(5)를 구하는 경우,

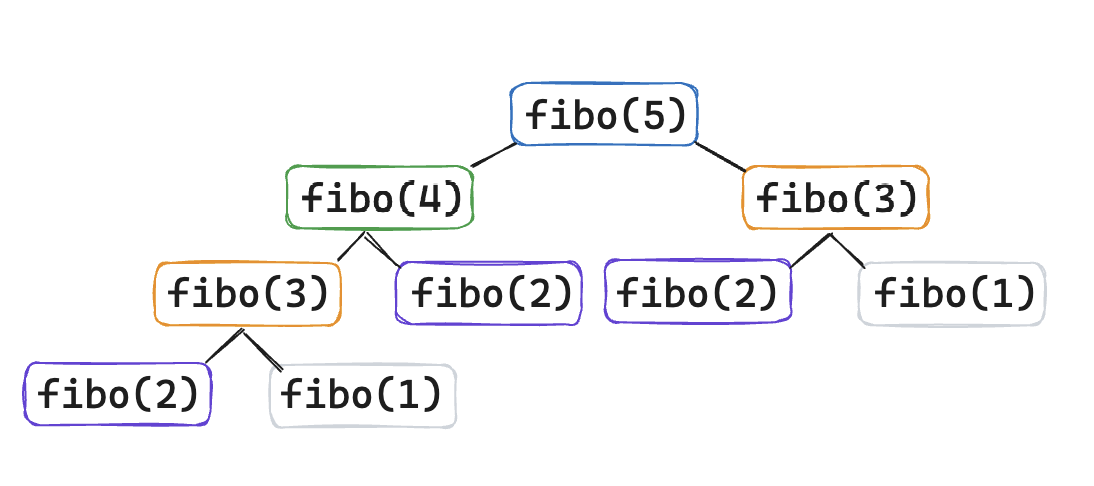
위 그림과 같이 fibo(1)과 fibo(3)은 2번, fibo(2)는 3번이나 반복 수행합니다. 사실 fibo(4) 쪽 트리의 계산만 해도 오른쪽 트리는 전부 중복이라 계산할 필요가 없습니다. 이런 중복을 없애서 성능을 최적화 하는 기법이 DP입니다.

function fiboDP(n, memo = {}) {
  if (n <= 2) return 1;
  if (memo[n]) return memo[n];

  memo[n] = fiboDP(n - 1, memo) + fiboDP(n - 2, memo);
  return memo[n];
}

이렇게, 한 번 계산한 값은 memo 객체에 n을 key로 하여 값을 저장하고, 같은 값이 필요하면 계산하지 않고 꺼내서 바로 사용할 수 있습니다.

DP를 사용해 계산값을 저장해 중복 계산을 없애면 O(n), 즉 fibo(4)쪽 트리만(여기서도 fibo(2)의 중복계산 없이) 계산하여 답을 도출할 수 있습니다.

🆚

전역 객체 memo

처음에 피보나치 수열에 메모이제이션을 접목할 때 다음과 같이 코드를 짰습니다.
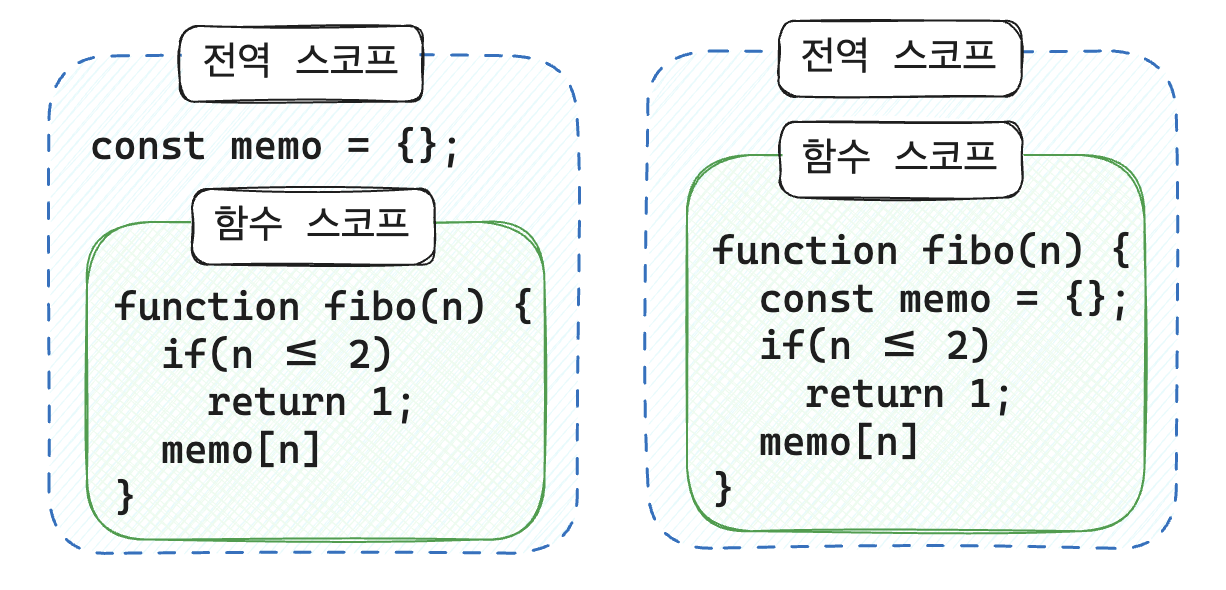
const memo = {}; 
function fibo(n) {
  if (n <= 2) return 1;
  if (memo[n]) return memo[n];
  memo[n] = fibo(n - 1) + fibo(n - 2);
  return memo[n];
}
momo{} 객체를 전역에 두고, 계산 결과를 저장하고 사용했습니다. 이 또한, 잘 작동하였습니다. 하지만 이러한 방식은 DP 원칙과 함수의 안정성을 해친다는 것을 알게되었습니다.

이를 이해하려면 “스코프” 개념을 알아야 합니다.
스코프는 변수가 선언되고, 접근할 수 있는 범위를 의미합니다. 쉽게 비유하자면, 전역 스코프는 거실에 있는 공용 냉장고이고 함수 스코프는 내 방의 개인 냉장고라고 할 수 있습니다.

공용 냉장고는 누구나 꺼내어 쓸 수 있습니다. 모두가 냉장고에 자기 음식을 넣었다 뺏다하면서 추적할 수 없고, 예상치 못한 값이 들어 있을 수 있습니다.

하지만 개인 냉장고는 다른 사람이 쉽게 접근하지 못해서 내가 넣은 음식과 꺼내 먹은 음식을 추적할 수 있고, 안에 어떤 게 들어있는 지 쉽게 예측할 수 있습니다.

따라서 스코프가 좁을 수록 코드의 안정성과 예측 가능성이 높아집니다.

전역에 memo 객체를 선언하게 되면 함수 내부의 결과 값이 외부로 노출되고, 외부 상태에 의존하게 됩니다. 다른 함수나 로직에서 의도치 않게 값을 바꿀 수 있고, 이전 실행 결과가 다음 실행에 영향을 주는 부작용(side-effect)이 발생할 수 있습니다.
예를 들어, fibo(5)를 계산하고 fibo(10)을 계산할 때, fibo(5)에서 계산한 값들이 memo객체 안에 값이 들어가 있고, 코드가 수정되고 다른 인풋 값으로 다시 호출할 때(fibo(10))에 다시 계산하지 않고 이전의 결과를 믿고 그대로 사용해 예상하지 못한 결과가 나올 수 있습니다. 따라서 다른 계산을 하기 전에 memo 객체를 초기화 할 필요성이 생깁니다.
함수는 함수형 원칙이라는 원칙을 가집니다. 입력만 결과에 영향을 주어야 한다는 원칙입니다. 위와 같은 코드는 함수 외부의 전역 스코프에 의존하면서 이러한 원칙을 어기고, 함수의 재사용성과 안정성이 깨집니다.
function fibo(n, memo = {}) {
  ...
}
이렇게 함수 인자로 memo객체를 전달하여 사용하면 항상 새로 시작하거나, 외부에서 전달할 때 직접 컨트롤 할 수 있습니다. 함수 내부에서만 memo 객체가 사용 되어 안전하고 입력만 결과에 영향을 주어 함수형 원칙이 잘 지켜집니다.

DP 최적화 문제

모든 문제에 DP를 사용할 수는 없습니다. DP를 적용하기 위해서는 두 가지 조건이 필요합니다.

같은 계산을 여러 번 반복하게 되는 구조로 중복되는 부분 문제가 존재해야 합니다.
작은 문제의 정답으로 큰 문제의 정답을 만들 수 있어야 합니다.

위 조건을 갖추었을 때, 작은 문제의 정답을 저장하고 재사용하는 전략이 필요합니다.

DP 문제 해결 전략

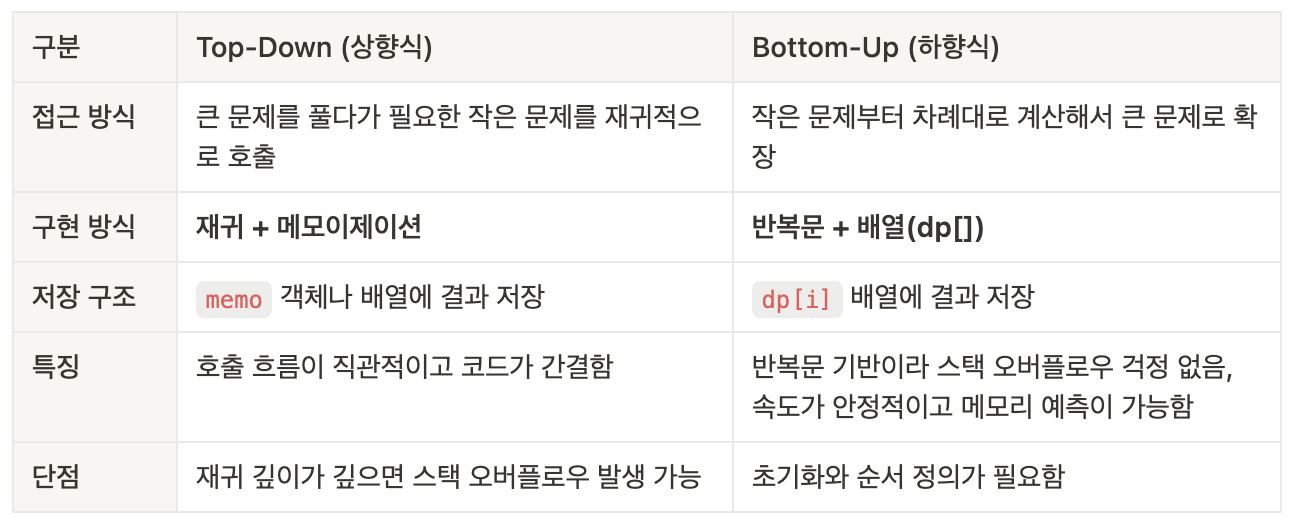
DP의 문제 해결 전략은 두 가지 방식이 있습니다. Top-Down(상향식)과 Bottom-Up(하향식)방식이 있습니다. 문제 해결 방향에 따른 분류입니다.

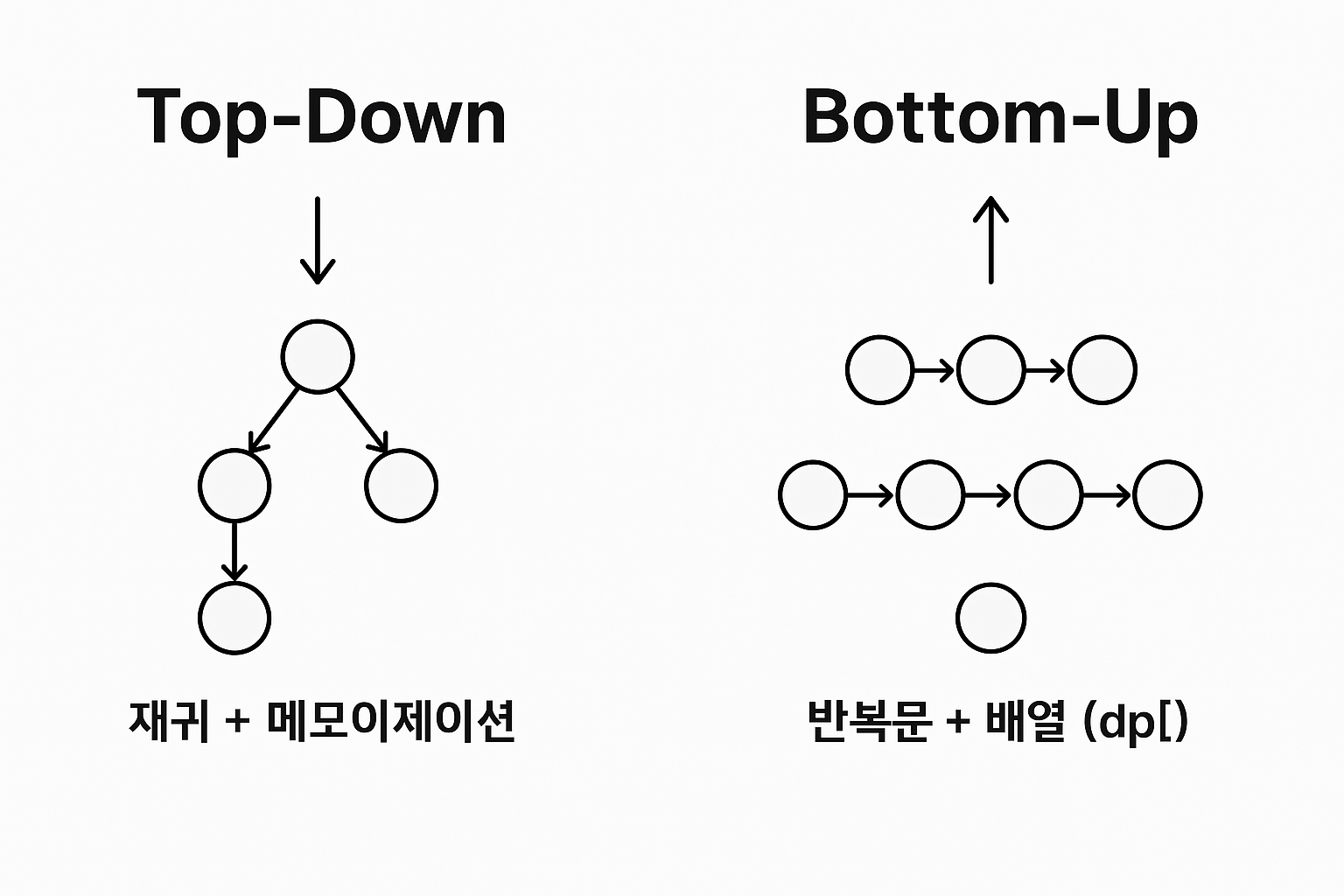
성능 면에서는 Bottom-Up 방식이 유리한 경우가 많지만, 문제의 구조를 파악할 때 Top-Down이 더 직관적이라서 좋습니다.

1. Top-Down 피보나치 예시

function fib(n, memo = {}) {
  if (n <= 2) return 1;
  if (memo[n]) return memo[n];

  memo[n] = fib(n - 1, memo) + fib(n - 2, memo);
  return memo[n];
}

계산한 값을 memo[n]에 저장하여 사용하고, 필요할 때만 계산합니다.
직관적이지만, 호출이 많으면 재귀이므로 stack overflow 위험이 있습니다.

2. Bottom-up 피보나치 예시

function fib(n) {
  const dp = [0, 1, 1];

  for (let i = 3; i <= n; i++) {
    dp[i] = dp[i - 1] + dp[i - 2];
  }

  return dp[n];
}

for문으로 순회하므로 작은 문제부터 차례로 해결하며, 배열을 앞에서부터 채워나갑니다.
재귀가 아니라 스택을 사용하지 않아, 안정적입니다.

🆚

재귀에서의 ‘Top-Down’, ‘Bottom-Up’ (참고)

재귀를 공부할 때도 Top-Down, Bottom-Up 방식이라는 말이 나옵니다. DP와 같은지, 차이점은 없는 지 궁금증이 생겼습니다.
우선, Top-Down, Bottom-Up이라는 말은 문제 해결 방향을 말합니다.

Top-Down: 큰 것부터 시작해서 점점 작게 내려감

Bottom-Up: 작은 것부터 시작해서 점점 키워나감

재귀함수는 큰 문제를 풀기 위해 작은 문제로 재귀를 호출합니다. 피보나치 재귀 함수에서 fibo(5)가 fibo(4)를 부르고, 또 fibo(3)을 부르면서 내려가는 구조(Top-Down)입니다. 계산은 return값이 쌓여서 돌아오면서 아래부터 올라옵니다(Bottom-Up).

DP에서도 같은 말을 쓰고, 예시도 같지만 핵심이 다릅니다. DP의 Top-Down은 한 번 계산한 결과를 저장해두는 것(메모이제이션)이 핵심입니다. Bottom-up은 반복문을 사용해 작은 문제의 답부터 계산해서 답을 쌓아 올리는 전략입니다.

결과적으로, 재귀에서는 호출 방향/계산흐름을 말하고 DP에서는 필요할 때만 재귀로 계산해서 저장/반복문으로 계산을 쌓아올리는 전략을 말합니다.