[ ᴀʟɢᴏʀɪᴛʜᴍ ] Recursive(재귀)와 Call Stack (호출 스택)

NewHa·2023년 8월 25일
algorithm
1

ᴀʟɢᴏʀɪᴛʜᴍ

목록 보기
1/14
post-thumbnail

🌱 Recursive Function ( 재귀 함수 )

👉🏻 재귀(再歸) : 주어진 문제를 해결하기 위해 하나의 함수에서 자신을 다시 호출하여 작업을 수행하는 방식. 어떤 루틴이나 프러시저가 자기 자신을 반복적으로 호출하여 문제를 풀어나가는 알고리즘. ( - Naver Dictionary)

함수를 정의할 때, 자기 자신을 다시 참조해 호출하는 알고리즘을 말한다.

👉🏻 구현 형태

// Implementing recursive 1
function recursive(input) {
  if(input > limit) return recursive(input -1); // 💫 recurrence relation
  else return limit // or specific value, 👈🏻 base case : 재귀 호출 종료
}

// Implementing recursive 2
function recursive(input) {
    if (input <= limit) return limit; // or specific value 👈🏻 base case : 재귀 호출 종료
    return recursive(input - 1); // 💫 recurrence relation
}
  • return 에서 함수 자기자신인 recursive()를 호출하고 있다.(= 재귀)

☀️ Requirements( 요건 )

A. Base case ( 종료식 )

더 이상 재귀호출을 하지 않아도 계산값을 반환할 수 있는 조건으로, 재귀 함수는 특정 입력에 대해 자기 자신을 호출하지 않는 조건으로 수렴해야한다. 제대로 명시하지 않으면 무한하게 함수를 호출하여 에러가 발생(stack exceeded error)하므로 반드시 적어야 한다.

🌿 Stack Exceeded Error ( RangeError )

Call Stack ( 호출 스택 )

V8(을 포함하는 대부분의 자바스크립트 엔진)은 무한 재귀와 과도한 메모리 사용으로 stackoverflow 및 잠재적 충돌을 방지하기 위해, 호출 스택(call stack) 크기에 제한을 두고 있다.

  • 대략 V8에서 수행할 수 있는 재귀 호출의 수는 Node.js : 약 11,034, Chrome : 약 10,402 정도 이다. 스택의 크기와 스택 프레임의 크기(매개 변수, 지역 변수 수량)에 따라 다르다.
  • call stack (호출 스택) : 함수 호출의 실행 컨텍스트를 추적하는 데이터 구조이다.

Stack Exceeded Error ( RangeError )

호출 스택의 최대 용량을 초과하는 오류이다.

  • python 에서는 메모리 제한을 두어서 최대 재귀 깊이 초과 오류(RecursionError : maximum recursion depth exceeded while calling a Python object)라 하는데, JavaScript 에서는 콜스택의 frame 수가 정해져 있어 범위 오류(RangeError : Maximum call stack size exceeded)라고 부른다.
  • 적절한 base case가 없거나, base case로 수렴하는 recurrence relation(점화식)이 부적절한 경우, 무한 재귀가 발생해 호출 스택 최대 용량을 초과하는 경우가 생긴다.
  • 이 외에도 실행되는 재귀 함수의 호출 횟수가 대략 10,000번을 넘어가는 경우 어느 정도 재귀 출력을 하다가 출력 오류가 발생한다.

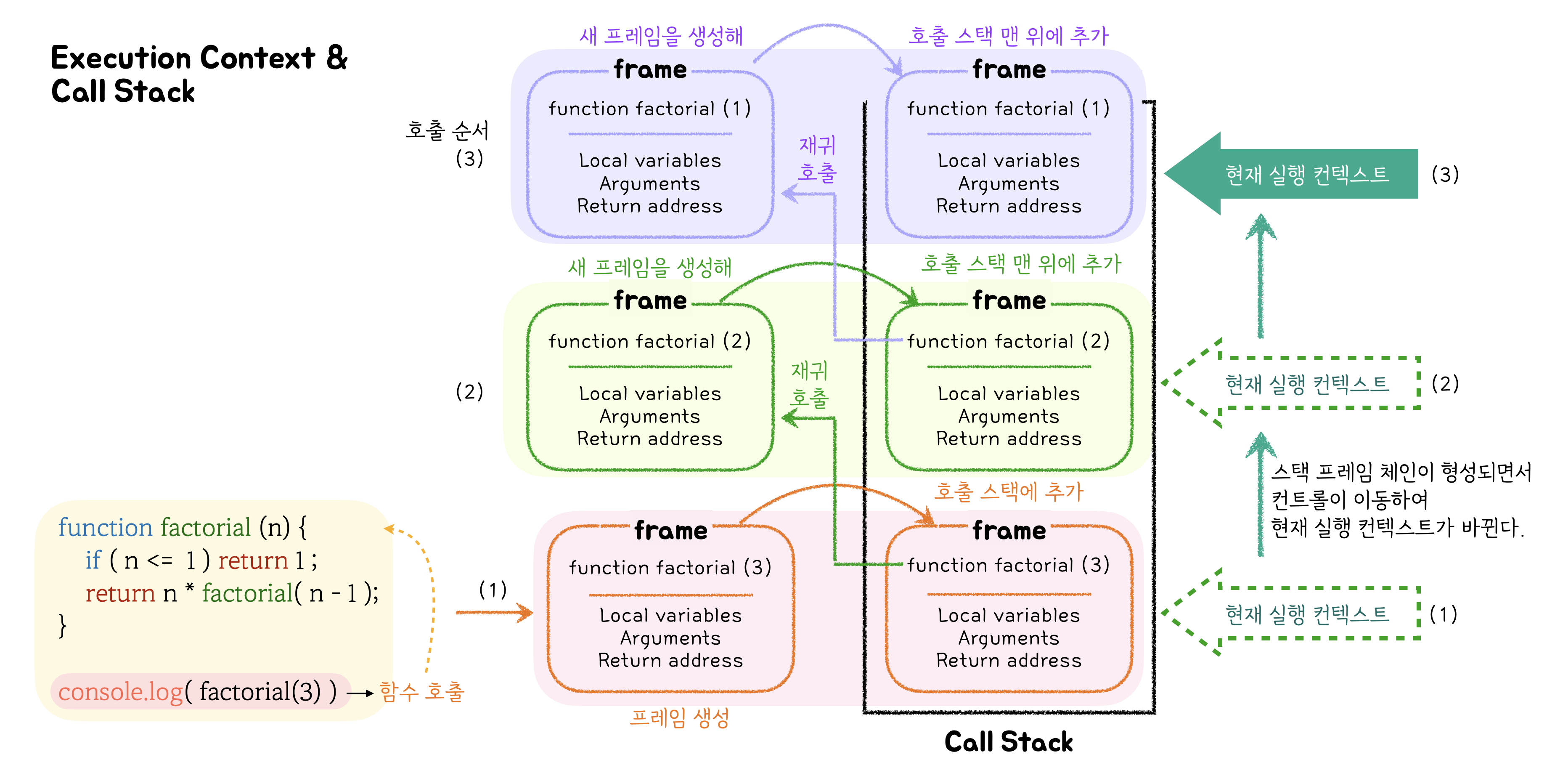
Execution context (실행 컨텍스트) & Stack (스택) 👉🏻 재귀 함수의 실행

실행 중인 함수의 실행 절차에 대한 정보는 해당 함수의 실행 컨텍스트(함수 실행에 대한 세부정보를 담고 있는 내부 데이터 구조)에 저장된다.

  • 함수가 호출 되면, 함수의 인수, 지역변수, 반환 주소를 포함하는 새 프레임이 생성되고 호출 스택 맨 위에 추가가 되고 실행된다.
  • 함수가 실행되다가 재귀 호출(함수 내부에서 중첩 호출, 서브 호출)이 있으면, 현재 함수의 실행을 일시 중지(대기)하고 중첩 호출된 함수의 새 프레임을 생성하고 호출 스택 맨 위에 추가해 실행한다.
  • 호출 스택에 새로운 프레임이 추가되면 스택이 깊어지면서 스택 프레임 체인을 형성하고, 컨트롤이 재귀 호출 순서에 따라 서로 다른 스택 프레임 사이를 이동하며, 현재 실행 컨텍스트가 바뀐다.
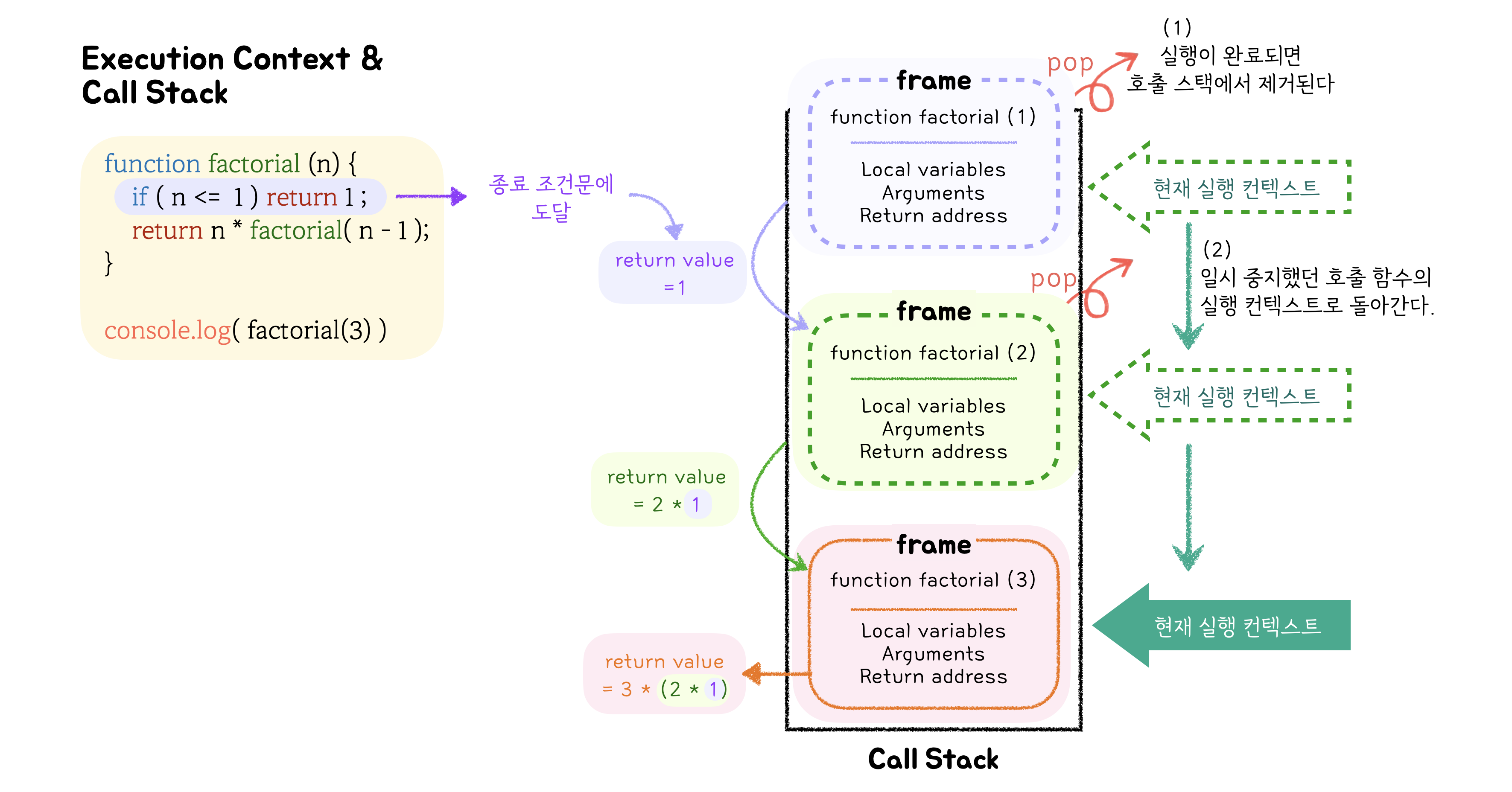
  • base case를 충족하면 재귀가 중지되고, 호출 스택 최상단의 서브 호출이 완료된다. return value를 호출 함수로 넘겨주고 해당 프레임은 실행스텍에서 제거(pop) 된다. 컨트롤이 스택 프레임을 통해 일시 중지했던 호출 함수의 실행 컨텍스트로 이동해 실행을 이어 나가며 return value를 도출한다.

B. Recurrence relation ( 점화식 )

점화식 : 특정한 함수를 자신보다 더 작은 변수에 대한 함수와의 관계로 표현한 것이다.

  • 자기 자신을 재귀적으로 호출 할 때 넘기는 인자를 명확히 해야 한다.
  • 재귀적으로 호출하여 도출되는 값들을 계속 넘겼을 때, 최종 문제의 답이 되도록 구현해야 한다.

☀️ Characteristics ( 특징 )

  • 재귀함수의 시간복잡도 = 재귀 호출 수 x 재귀 함수 하나당의 시간복잡도

  • 코드가 간결하여 가시성이 좋고, 구현하기 쉽고 유지보수가 쉽다.

  • 약 10,000번 정도(stack size) 까지만 재귀 호출이 가능하므로, 많은 호출이 필요할 때는 사용할 수 없다.

  • 시간 복잡도와 별개로, call stack 과정에서 재귀 호출이 속도가 느리고 메모리를 크게 차지 한다.

    🌿 Why are recursive functions slow and memory-intensive?

    function call overhead ( 함수 호출 오버헤드 )

    함수 호출을 설정하고 관리하는 데 필요한 추가 계산 작업을 나타내는 것으로, 재귀 처리시 함수 호출의 성능과 관련이 있다. (But, stack과는 별개의 문제라 RangeError의 원인은 되지 않는다.)

    • 함수 호출에는 고유한 overhead 가 있고, 여기에는 실행 컨텍스트 설정, 로컬 변수 관리, 반환 값 처리 등의 작업이 포함되어 있다. 재귀 함수에서 이 overhead는 각 호출마다 곱해져 누적되는 영향을 미친다.
      • 실행 컨텍스트 설정 : 실행 중인 명령을 추적하고, 반환 값을 처리하는 등의 적절한 실행을 위한 관련 정보를 포함해 설정한다.
      • 로컬 변수 관리 : 함수를 실행하기 위해 함수 내 로컬 변수에 메모리 공간을 할당하고 초기화하는 작업을 포함한다.
      • 반환 값 처리 : 함수 실행이 완료되어 값이 나오면 호출된 곳으로 반환하고 함수의 스택 프레임 정리를 관리한다.
    • 재귀 함수가 반복적으로 호출됨에 따라 스택 프레임이 호출 스택에 추가되어 함수 호출 체인이 생성되는데, 다수의 스택 프레임을 관리하기 위해 메모리 할당과 해제가 지속적으로 필요하며 추가적인 overhead가 발생한다.
    • 반환 값과 실행 흐름을 처리하기 위해 실행 컨텍스트가 자주 전환되는데, 서브 함수의 실행상태를 저장하고, 호출 함수의 상태를 복원하는 작업이 이루어지면서, overhead가 추가된다.

🌿 vs. 반복문으로 구현하는 경우

  • 모든 재귀 알고리즘은, 재귀 없이 반복문으로도 구현할 수 있다.
  • 전체 반복 과정을 서술해야 하므로, 구현이 복잡하고 시간이 오래걸린다.
  • 재귀보다 직관적인 가시성이 떨어진다.
  • 하지만 속도가 빠르고 호출 수의 제한이 없다.

🪴 Implementing Recursions ( 재귀로 문제 해결 )

재귀를 사용하는 상황

  • 주어진 문제를 비슷한 구조의 더 작은 문제로 나눌 수 있는 경우에
  • 중첩된 반복문이 많거나, 중첩 횟수를 예측하기 어려운 경우

재귀적으로 사고하기 (👉🏻 재귀 함수 구현하기)

  1. 함수를 명확하게 정의해야 한다. 따라서 함수의 입력값(인자)와 출력값을 명확하게 정의해야 한다.
  2. 문제를 더 작고 유사한 하위 문제로 나눌 수 있는 방법을 결정해 나누며, 어디까지 계산하고 자기 자신에게 넘겨 줄지 recursive case를 설계해야 한다.
  3. 가장 작은 단위로 문제를 쪼개 함수가 자신을 호출할 필요 없이 결과를 직접 반환할 수 있는 특정한 경우를 식별해 base case(탈출 조건)를 설정한다.
  4. 하위 문제에 대한 해결 방법을 사용해 복잡한 문제를 해결할 방법을 결정한다.

🪴 Using Recursion ( 재귀의 활용 )

🐾 factorial 팩토리얼

  • n! = n x (n - 1)! = 1 x 2 x 3 x ... x (n - 1) x n
  • 시간복잡도 : O(n - 1)
// 반복문으로 구현한 팩토리얼
function factorial_iterative(n) {
  let result = 1;
  for (let i = 1; i <= n; i++) {
    result *= i;
  }
  return result
}
// 재귀로 구현한 팩토리얼
function factorial_recursive(n) {
  if(n <= 1) return 1;
  return n * factorial_recursive(n - 1);
}

🐾 fibonacci 피보나치

// 반복문으로 구현한 피보나치
function fibonacci_iterative(n) {
  let result = 1;
  for (let i = 1; i <= n; i++) {
    result += i;
  }
  return result
}
// 재귀로 구현한 피보나치
function fibonacci_recursive(n) {
  if( n === 1 ) return 1;
  return fibonacci_recursive(n - 1) + fibonacci_recursive(n - 2);
  //return fibonacci_recursive(n - 1) + n
}
// 가우스 덧셈을 사용한 수학적 풀이
function fibonacci_gauss(n) {
  return n * (n + 1)
}

🌈 Finish

  • 재귀 함수가 한 번에 자기 자신을 여러번 호출하는 케이스(ex. fibonacci_recursive)는 시간 복잡도가 급격하게 늘어나므로 재귀보다 DP(Dynamic Programming)를 이용하는 것이 좋다. DP 또한 작은 문제로 나누어 복잡한 문제를 해결하는 알고리즘인데, 재귀의 문제점인 중복 호출을 memoization 이나 tabulation 으로 해결하여 더 효율적이다.

  • 편의상 실행 컨텍스트를 화살표로 표현해 컨트롤을 옮겨서 표현했지만, 사실상 실행 컨텍스트도 하나의 스택이고, 그 스택에서 pop 해와 현재 실행 컨텍스트가 되는 부분이 아직 헷갈리고, 어떻게 표현해야 할 지 조금 더 고민하고 후에 포스트를 수정해야 겠다.

  • 재귀 호출시 넘겨받는 인자 수에 따라서도 실행시간이 크게 차이가 나는데, 이것이 call stack size 때문이라는 것을 알게 되었다. stack size에 대해 찾아보며 자바스크립트 엔진 중 대표격인 V8의 자바스크립트 호출시 stack frame 구조에 대한 페이지를 보게되었는데, 아직 이해하기엔 모르는 것들이 많아서 더 공부할 필요성을 느꼈다. JavaScript 구동 방식에 대해 찾아보면서 보게된 stack 과 heap 동작에 대해서도 따로 정리해야 겠다!!

👀 Reference

profile
NewHa
백 번을 보면 한 가지는 안다 👀
다음 포스트

[ ᴀʟɢᴏʀɪᴛʜᴍ ] Bubble Sort ( 버블 정렬 )

0개의 댓글