🌱 Heap ( 힙 )
👉🏻 힙 (Heap, '무언인가를 차곡 차곡 쌓아올린 더미') : 힙 자료구조는 여러 개의 값들 중 최댓값 및 최솟값을 빠르게 찾아내기 위해 고안된 완전 이진 트리에 기반한 특별한 이진 트리 데이터 구조입니다. 부모 노드의 값이 자식 노드의 값보다 항상 크거나 작은 이진트리를 말합니다. 이를 위키백과에서는 일종의 반정렬 상태(느슨한 정렬상태)를 유지한다고 표현합니다.
-
'반정렬', '느슨한'이라는 수식어가 붙는 이유는 부모 노드와 자식 노드의 대소관계만 관계가 있을 뿐, 형제 노드 사이에는 순서나 관계가 없기 때문입니다.
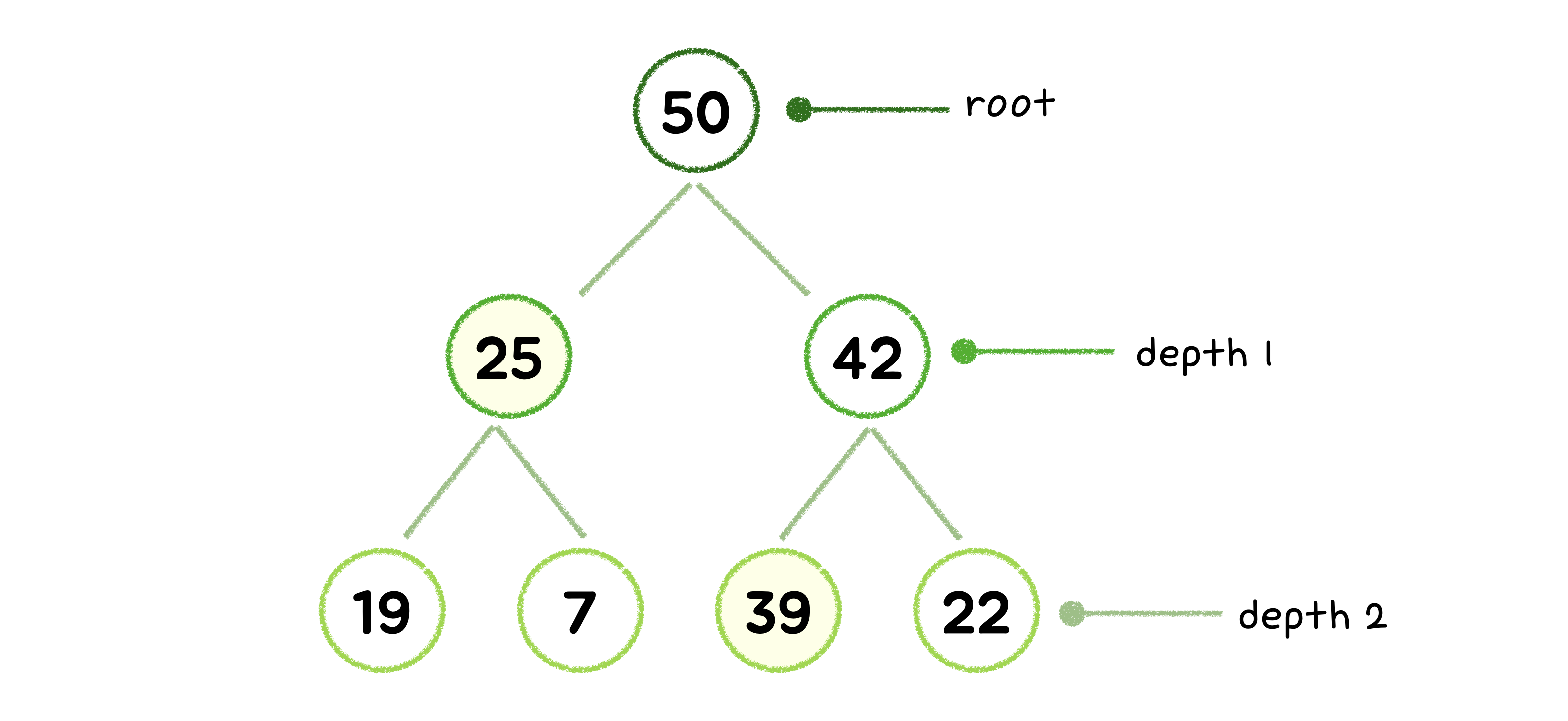
(Max-heap을 기준) 위 그림과 같이depth 1의 숫자가 반드시 전체 heap 에서 두번째, 세번째로 큰 숫자라는 보장이 없습니다. 또한 왼쪽과 오른쪽 간의 순서가 존재하지 않습니다. 오로지 부모 노드의 값보다 크거나 작게 정렬이 되면 족합니다. 따라서 완전한 정렬은 아닌 반정렬, 느슨한 정렬 상태라고 합니다.👉🏻 따라서 완전한 정렬이 아니므로 탐색에는 적합하지 않습니다. 특정 요소를 검색(탐색)하는 경우에는 반드시 전체를 순회해야 해서 O(n)의 시간복잡도를 가지게 됩니다. (완전한 정렬이라면 형제 노드 사이에서도 대소관계가 명확하므로 매 depth마다 특정 요소와 비교해 한 쪽으로만 내려가면서 탐색하므로 O(log n)의 시간복잡도를 가지게 됩니다.)
☀️ Type of Heap ( 유형 )
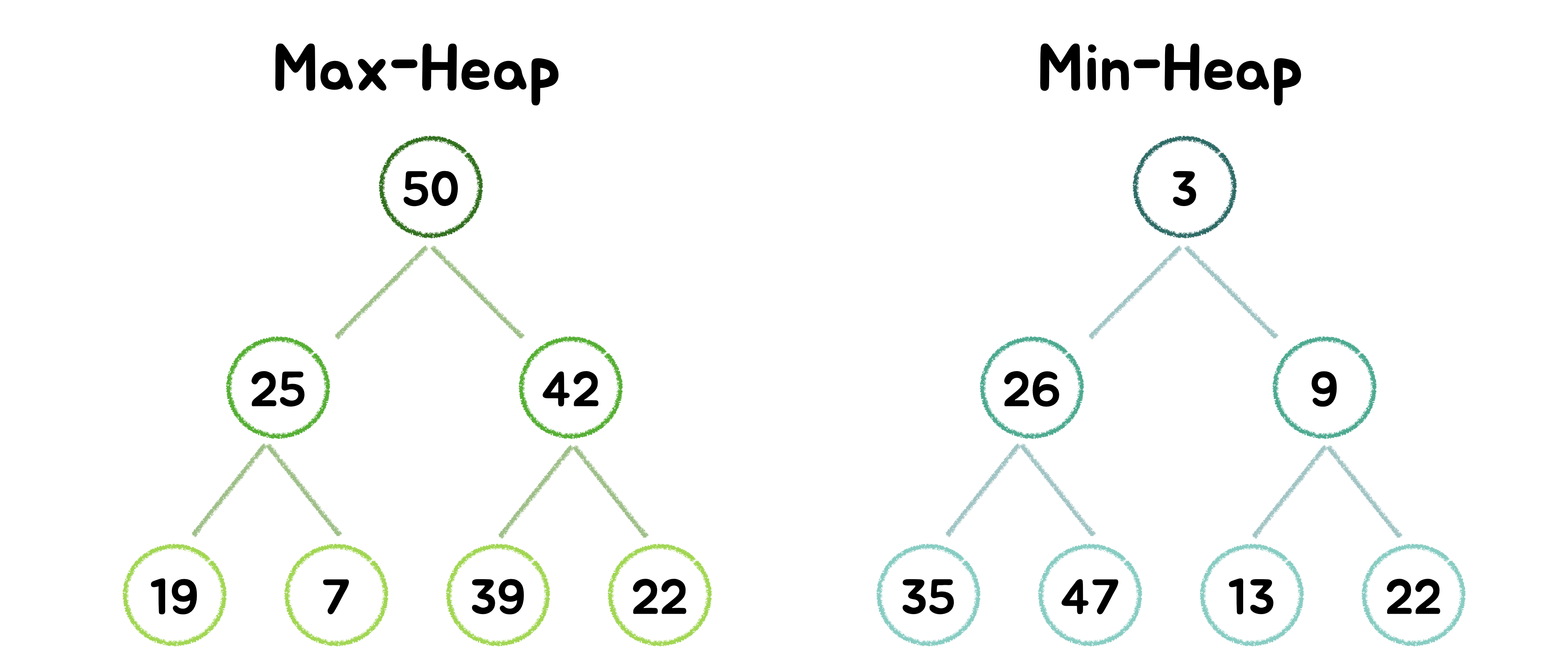
Max-heap ( 최대 힙 )
- 루트 노드의 값은 모든 하위 노드 중 가장 커야 하고, 하위 트리에서도 동일해야 합니다. 👉🏻 루트 노드의 값이 노드들 중 가장 큰 값임을 보장합니다.
- 내림차순 우선순위를 사용합니다.
- 가장 큰 요소가 우선순위를 가지고, 힙에서 가장 먼저 pop() 됩니다.
Min-heap ( 최소 힙 )
- 루트 노드의 값은 모든 하위 노드 중 가장 작아야 하고, 하위 트리에서도 동일해야 합니다. 👉🏻 루트 노드의 값이 노드들 중 가장 작은 값임을 보장합니다.
- 오름차순 우선순위를 사용합니다.
- 가장 작은 요소가 우선순위를 가지고, 힙에서 가장 먼저 pop() 됩니다.
☀️ characteristic of Heap ( 특징 )
- 표준적인 자료구조는 트리를 효율적으로 표현하도록 배열을 사용합니다. 배열의 위치를 기반으로 heap 구조를 모형화하여 위치에 상응하는 값을 보여줄 수 있습니다 (포인터를 필요로 하지 않게 됩니다).
👉🏻 왼쪽 자식 노드는2n + 1, 오른쪽 자식 노드는2n + 2의 index를 가집니다.
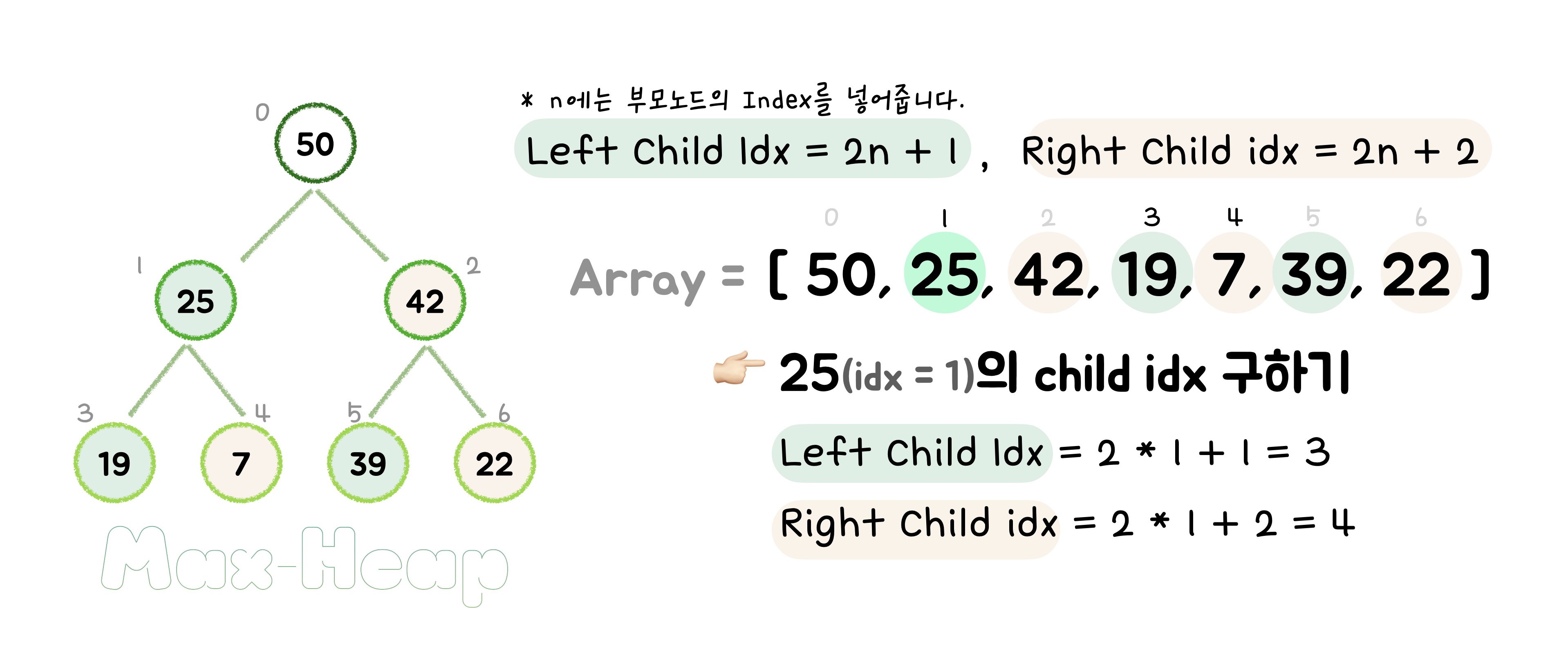
- 반대로 계산하여 부모 노드의 인덱스도 알아낼 수 있습니다. 부모 노드의 index는
Math.floor((idx - 1) / 2)로 구할 수 있습니다. - 같은 depth 에서는 왼쪽 노드가 언제나 먼저 채워집니다. ( 완전 이진 트리에 기반하므로 )
🙆🏻♀️ 장 점
- 요소를 효율적으로 삽입하고 삭제할 수 있습니다.
👉🏻 삽입과 삭제 모두O(log n)의 시간복잡도를 가지며, 이 경우 heap의 특징을 유지하도록 재구조화하는 heapify 프로세스가 동작합니다.🌿 시간복잡도 O(log n)
삽입과 삭제 모두 tree의 높이만큼 비교를 하게 되는데, 완전 이진 트리의 높이는 항상 log입니다. 이는 비교를 할 때 부모 노드의 값만 비교를 한다는 뜻입니다. 노드의 갯수는 완전 이진 트리 이므로 높이가 늘어날 수록 노드의 갯수는 2배씩 늘어납니다. 노드의 갯수가 2배가 들어나도 비교횟수는 1번만 늘어난다는 뜻입니다. 따라서 노드의 갯수 n이 늘어나는 것에 비해 비교횟수는 아주 천천히 늘어납니다.
- 최댓값 혹은 최솟값에 접근(peak)을 보장하여 극단 값을 찾는 문제에 적합합니다.
- 완전 이진 트리 구조에 저장하여 언제나 가장 작은 공간을 차지해 최적의 용량을 가진다.
🙅🏻♀️ 단 점
- 특정 요소 순서를 유지하도록 설계되어 데이터 구조가 유연하지는 않습니다.
- 최상위 요소에 접근하는 것은 효율적이나, 그 외의 특정 요소를 검색하려면 전체 트리를 탐색해야 해 적합하지 않습니다. (시간복잡도
O(n)이 걸립니다.) - 힙이 구성되거나 수정될 때 동일한 요소의 상대적 순서가 바뀔 수 있어 안정적인 데이터 구조는 아닙니다.
- 동적 메모리 할당이 필요해, 메모리가 제한된 시스템에서는 어려울 수 있으며, 할당된 메모리를 관리하는 것에서 오류가 발생하기 쉽습니다.
- 최악의 경우
O(n log n)의 시간복잡도를 가지므로, 더 빠른 알고리즘이 필요하다면 적합하지 않을 수 있습니다.
🪴 적 용
- 우선순위 큐 : 일반적으로 우선순위 큐를 구현하는데 사용됩니다. 우선순위가 가장 높은 요소에 지속적으로 접근할 수 있으므로 우선순위가 필요한 작업이나 이벤트를 관리하기 위한 효율적인 데이터 구조가 됩니다. 👉🏻 부상정도에 따른 환자치료 순서, 작업 스케줄링 등에 쓰입니다.
- 힙 정렬 알고리즘 : 힙 정렬 알고리즘의 기초입니다. 👉🏻 Database Indexing, 수치분석 등
- 그래프 알고리즘 : Dijkstra, Prim, Kruskal 알고리즘을 포함한 다양한 그래프 알고리즘에 사용됩니다. 대게 우선순위 큐 구현이 필요합니다.
☀️ Implement of Heap ( 구현 )
🪴 Max-Heap
주석으로 과정을 자세하게 설명해놓았습니다.
👉🏻 heap 생성
// 노드를 만들어 그냥 배열에 저장하기만 하면 되므로, 빈 배열을 생성해준다.
class MaxHeap {
constructor() {
this.arr = [];
}👉🏻 root node return ( root 요소 반환 ) - O(1)
getMax() {
return this.arr[0];
}👉🏻 insert() ( 삽입 ) - O(log n)
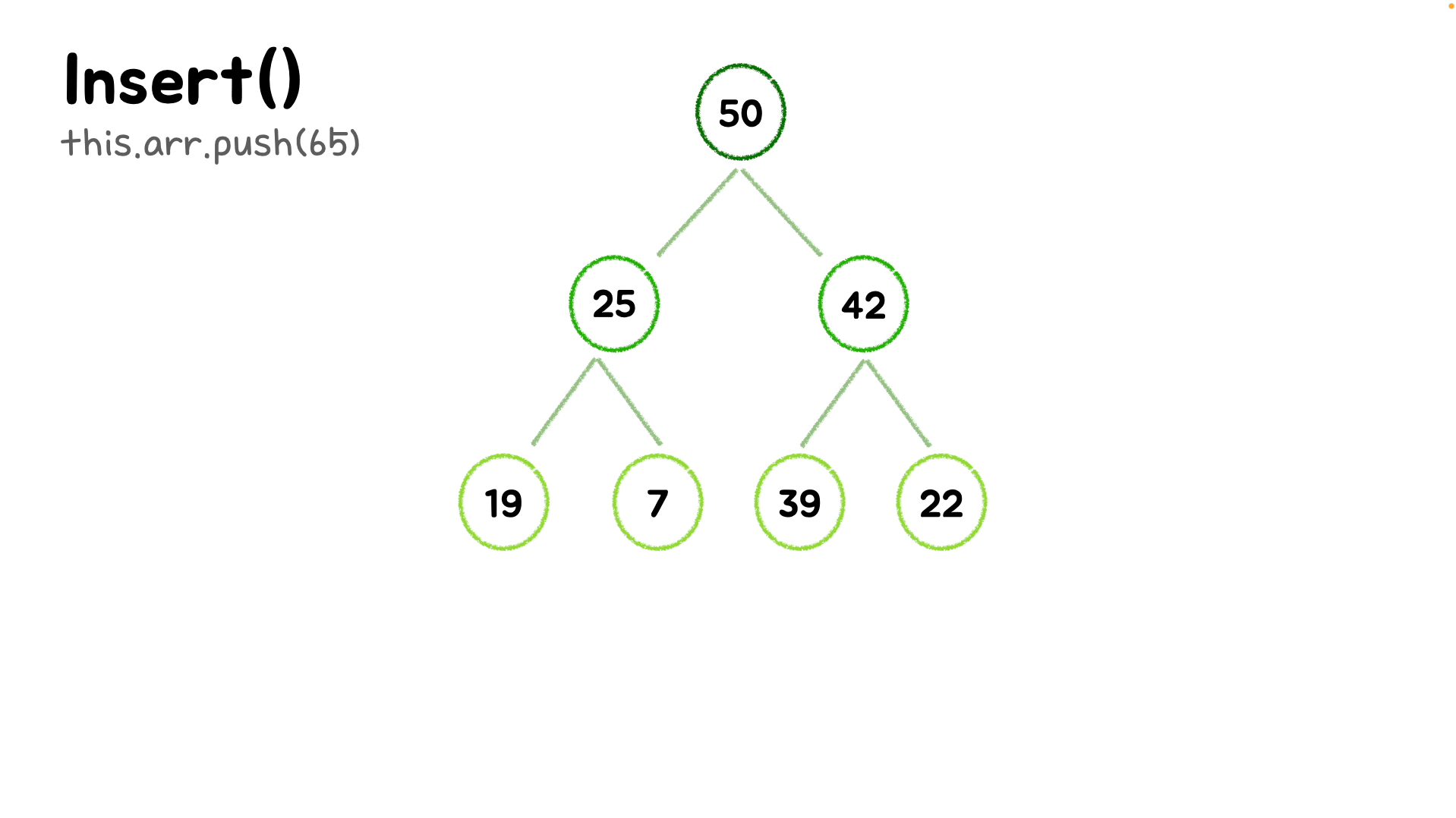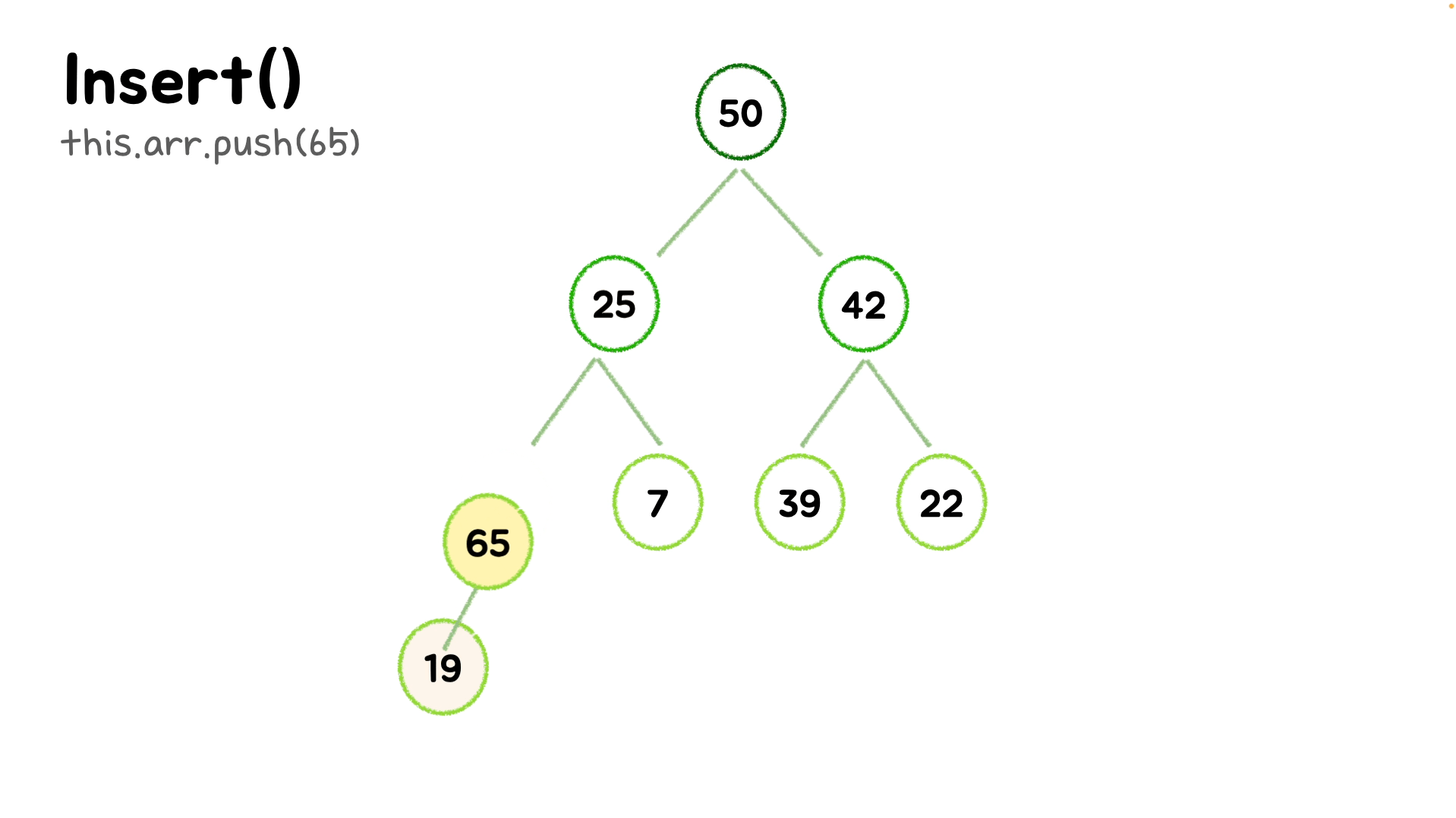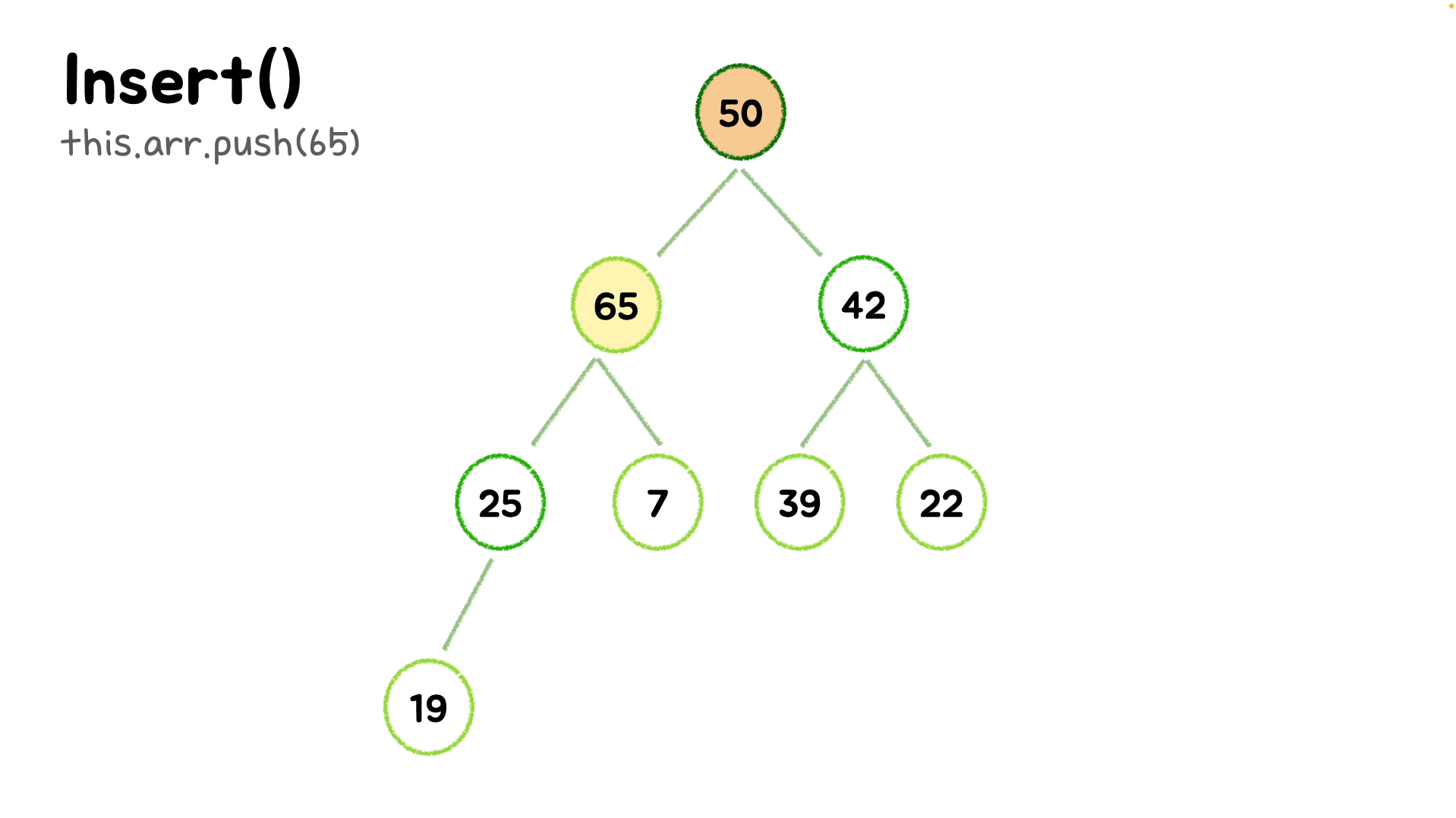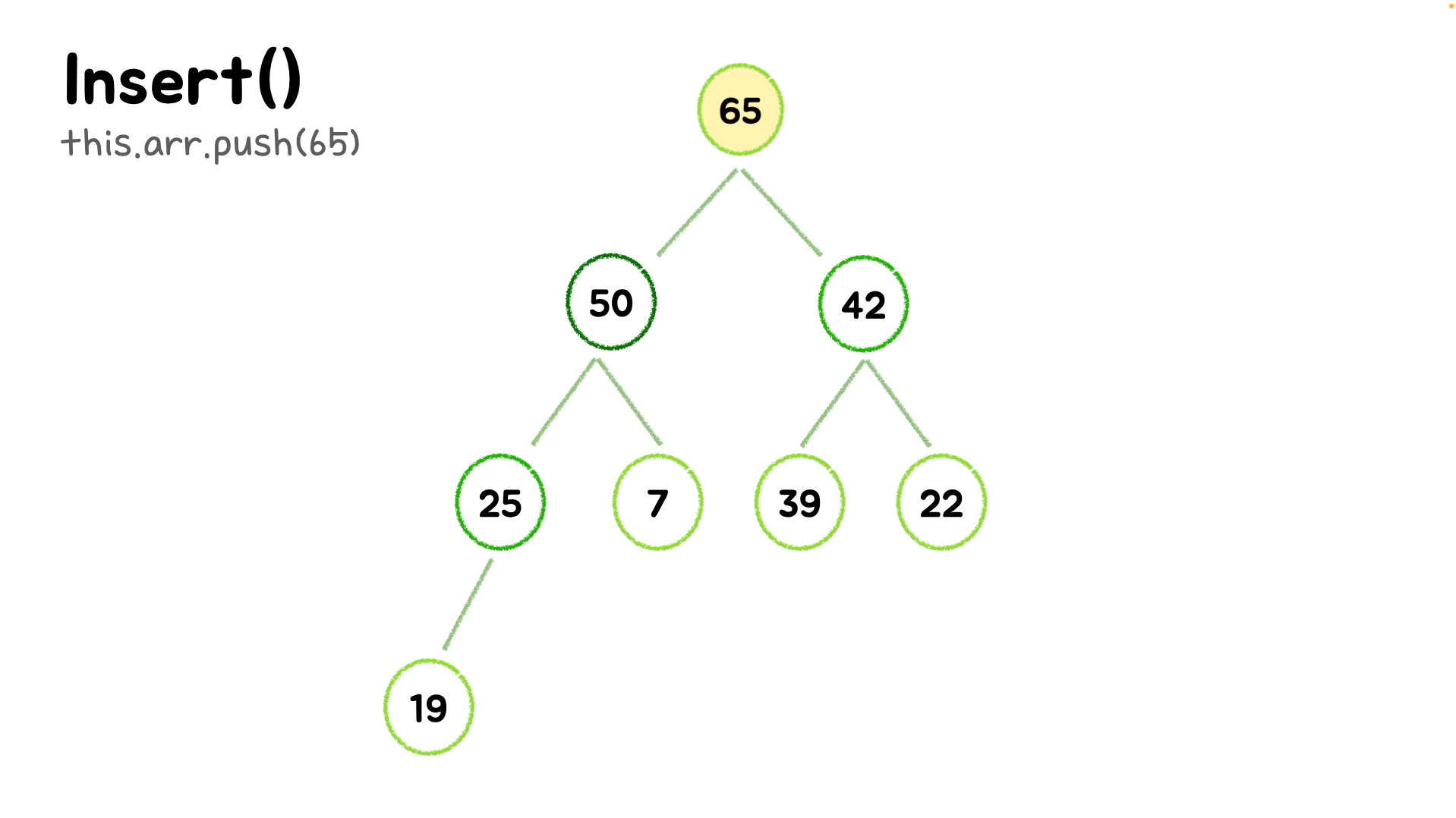
insert(element) {
// 언제나 맨 뒤에 값을 삽입하므로 push를 해준다.
this.arr.push(element);
// 이후 bubbleUp이라고 불리는 heapify 과정을 진행해 준다.
// 즉, 추가한 값의 올바른 위치를 찾아가는 과정이다.
// 이 안에서 과정을 정의해도 되지만 따로 method로 정의하는 게 깔끔!✨
this.bubbleUp();
}
bubbleUp() {
// 마지막 요소를 찾는다.
let idx = this.arr.length - 1;
// 마지막 요소의 값을 저장한다.
const element = this.arr[idx];
while(idx > 0){
// 자식노드의 idx를 구하는 식을 거꾸로 해 부모노드의 index를 구할 수 있다.
let parentIdx = Math.floor((idx - 1) / 2);
// 부모노드의 값을 저장한다.
let parent = this.arr[parentIdx];
// 부모노드의 값보다 작거나 같으면 동작을 멈춘다. (올바른 위치이므로)
if (element <= parent) break;
// 아니라면 부모노드 인덱스의 값과, 현재 인덱스의 값을 바꾸어 SWAP!
this.arr[parentIdx] = element;
this.arr[idx] = parent;
// 인덱스를 조정해준다.
idx = parentIdx;
}
}👉🏻 delete() ( 삭제 ) - O(log n)
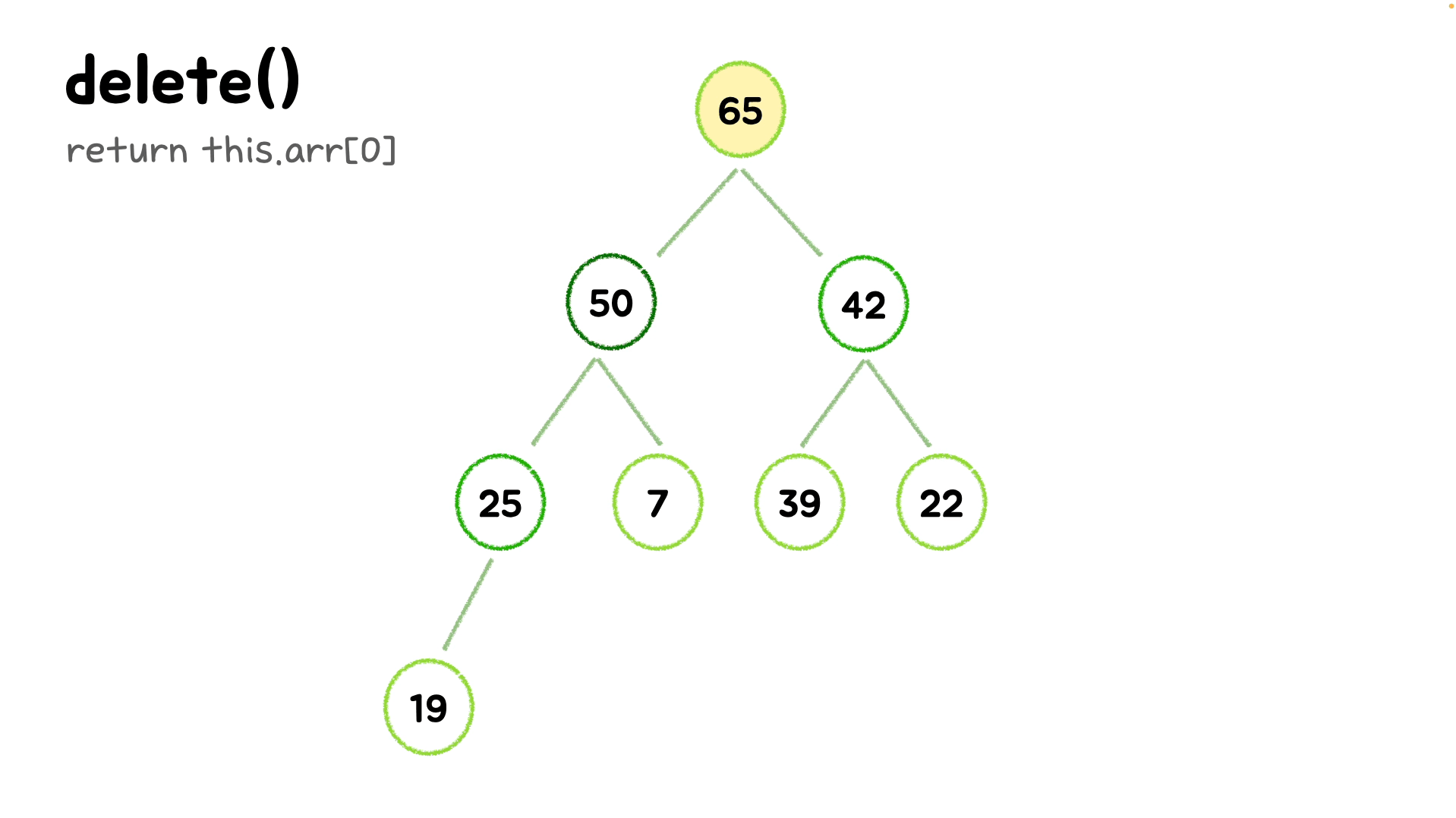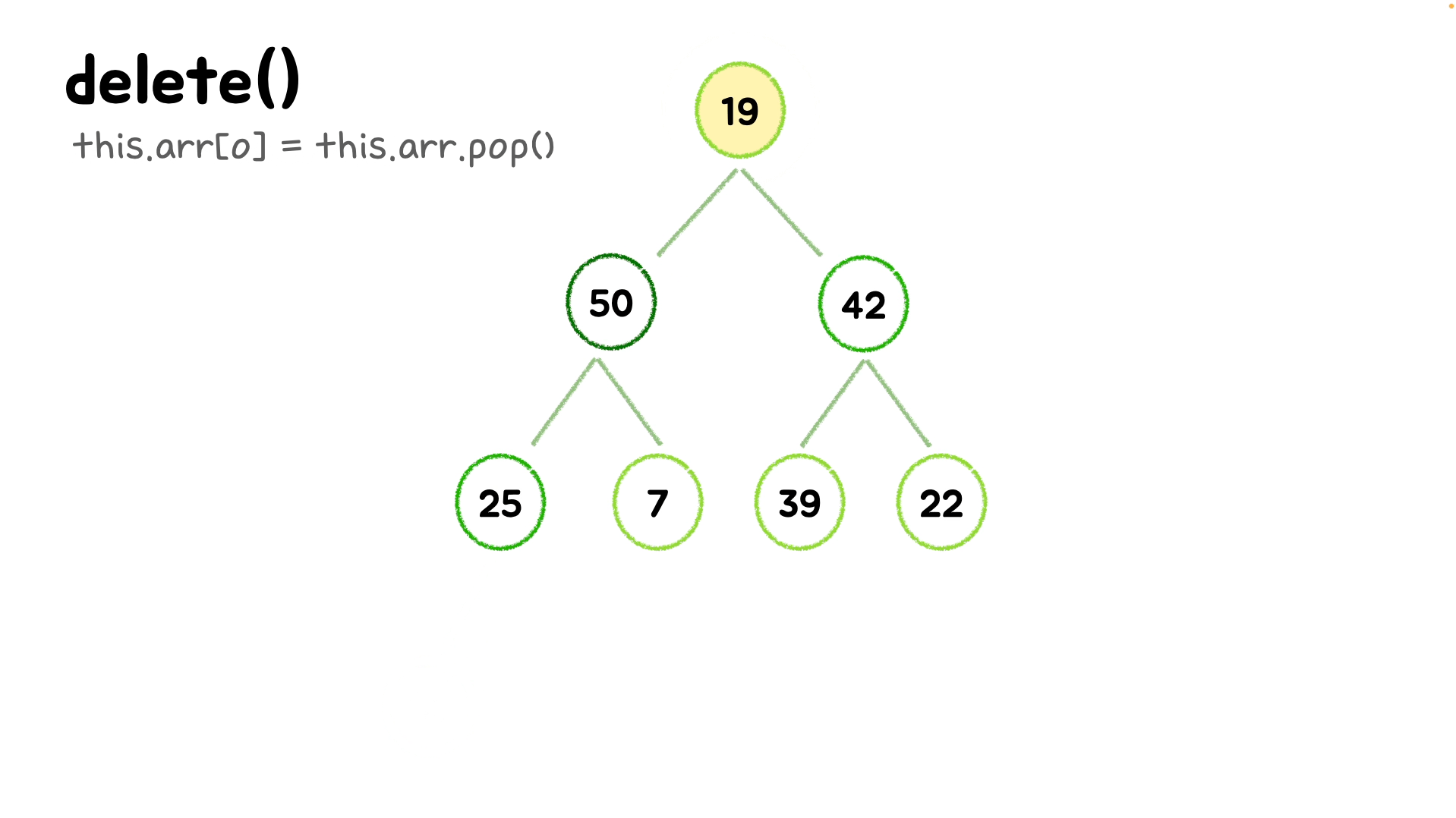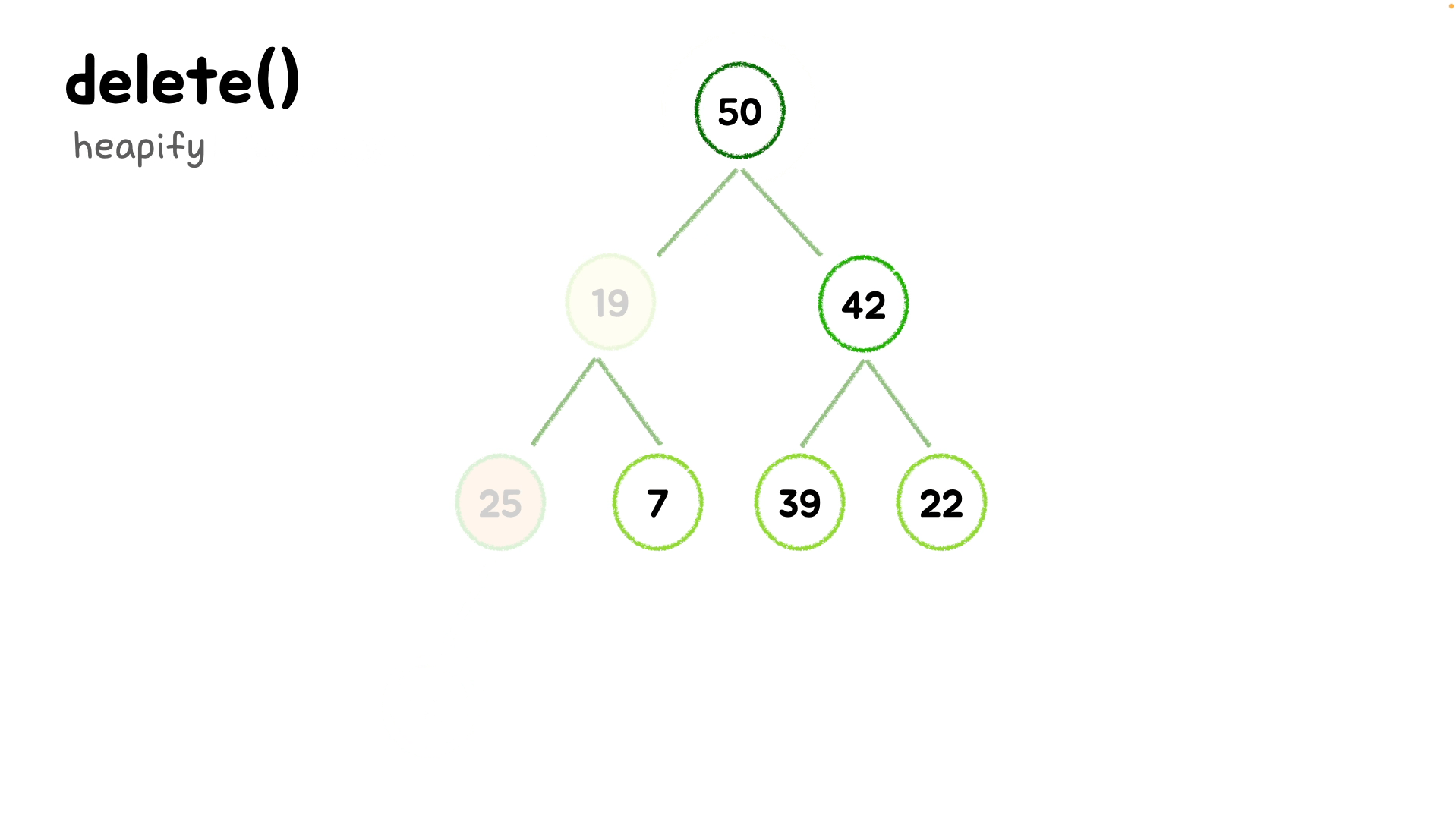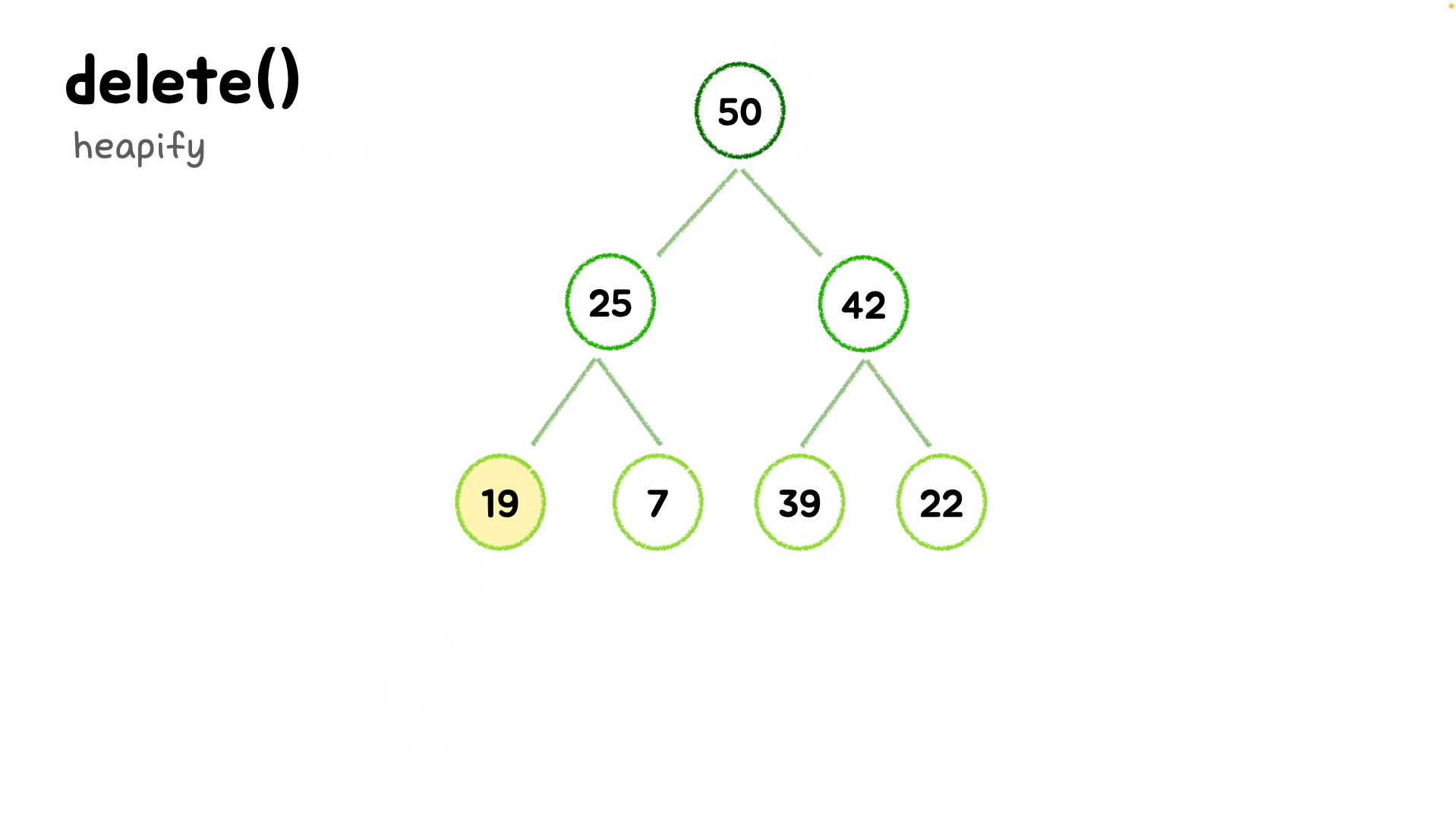
✔️ bubbleDown()시에 왼쪽 노드의 값과 오른쪽 노드의 값을 비교해 더 큰 값과 swap 합니다.
delete() {
// 첫번째 노드인 가장 큰 값을 저장해 후에 출력해준다.
const max = this.arr[0];
// 마지막 요소를 제거해 저장한다.
// 참고 : 이때 end가 마지막 요소라면 pop 하고 다시 push로 넣어준다.
const end = this.arr.pop();
// 만약 배열의 길이가 없다면 바로 max를 반환하고, 배열의 길이가 남았다면 end를 root 자리로 올리고 bubbleDown 과정을 진행한다.
if (this.arr.length > 0) {
// 첫번째 요소로 마지막 요소를 넣는다.
this.arr[0] = end;
// heapify 과정으로 이번에는 0번 인덱스에 있는 요소의 위치를 찾아 순회해준다.
// 이 안에서 과정을 정의해도 되지만 따로 method로 정의하는 게 깔끔!✨
this.bubbleDown();
};
// 삭제하는 가장 큰 값(루트 노드의 값)을 반환해준다.
return max;
}
bubbleDown() {
// 첫번쨰 인덱스부터 순회하며 내려갈 예정
let idx = 0;
const length = this.arr.length;
// 현재 인덱스의 요소값을 저장해준다.
const element = this.arr[idx];
while(true) {
// 자식 노드의 인덱스를 구해준다.
let leftChildIdx = 2 * idx + 1;
let rightChildIdx = 2 * idx + 2;
// 바로 value[leftChildIdx]로 값을 넣을 수 없다.
// 구한 자식노드의 인덱스가 범위내인지, 유효한지 확인이 필요하다.
let leftChild, rightChild;
let swap = null;
// 유효성검사
if(leftChildIdx < length) {
// 조건을 통과해 유효범위내의 인덱스라면 값을 저장해주고,
leftChild = this.arr[leftChildIdx];
// 만약 값이 현재값(원래 마지막요소였던 값)보다 크다면 SWAP해주기 위해 인덱스를 저장한다.
if(leftChild > element) {
swap = leftChildIdx;
}
}
// 오른쪽 노드도 유효성을 검사하고, 오른쪽 자식 노드와 자리를 바꿔야 하는 경우인지 확인한다.
if(rightChildIdx < length) {
rightChild = this.arr[rightChildIdx];
// 왼쪽 노드의 값이 더 크지 않았는데 오른쪽 노드의 값이 더 큰 경우나
// 왼쪽 노드의 값이 더 컸음에도 오른쪽 노드의 값이 왼쪽 노드의 값이 더 큰 경우
if((swap === null && rightChild > el) ||
(swap !== null && rightChild > leftChild)) {
// SWAP할 인덱스로 오른쪽 노드의 인덱스를 넣어준다.
swap = rightChildIdx;
}
}
// swap에 아무런 값도 들어있지 않다면, 올바른 위치인 것!!
if (swap === null) break;
// 아니라면 swap 해준다
this.arr[idx] = this.arr[swap];
this.arr[swap] = element;
}
}
}🪴 Min-Heap
👉🏻 heap 생성
class MinHeap {
constructor() {
this.arr = [];
}👉🏻 root node return ( root 요소 반환 ) - O(1)
getMin() {
return this.arr[0];
}👉🏻 insert() ( 삽입 ) - O(log n)
insert(element) {
this.arr.push(element);
// 👉🏻 이번엔 heapify를 내부에서 정의해 봄.
// 마지막 요소의 인덱스를 구한다.
let idx = this.arr.length - 1;
//index가 0보다 큰 동안
while (idx > 0) {
// 부모 노드의 인덱스를 구하고,
let parentIdx = Math.floor((idx - 1) / 2);
// 만약 부모노드의 값이 마지막 요소의 값보다 크면 멈추고
if(this.arr[parentIdx] > this.arr[idx]) brak;
// 아니면 요소들을 SWAP!!
[this.arr[idx], this.arr[parentIdx]] = [this.arr[parentIdx], this.arr[idx]];
idx = parentIdx;
}
}👉🏻 delete() ( 삭제 ) - O(log n)
delete() {
// 요소가 하나라면 pop으로 바로 반환한다.
if (this.arr.length === 1) {
return this.arr.pop();
}
// 가장 작은 루트 노드의 값을 저장하여 반환한다.
let min = this.arr[0];
// 마지막 요소와 첫번째 요소를 바꾼다.
this.arr[0] = this.arr[this.arr.length-1];
// 마지막 요소를 제거하고
this.arr.pop();
// heapify 함수를 부른다.
this.bubbleDown();
return min;
}
bubbleDown() {
let idx = this.arr.length - 1;
let length = this.arr.length;
if (length === 1) return;
let leftChildIdx = 2 * idx + 1;
let rigthChildIdx = 2 * idx + 2;
let min = idx;
if (leftChildIdx < length && this.arr[leftChildIdx] < this.arr[idx])
min = leftChildIdx;
if (rigthChildIdx < length && this.arr[rigthChildIdx] < this.arr[min])
min = rigthChildIdx;
if (min !== idx)
{
[this.arr[idx], this.arr[min]] = [this.arr[min], this.arr[idx]]
this.bubbleDown(min);
}
}
}🌱 Priority Queue ( 우선순위 큐 )
👉🏻 우선순위 큐 (priority queue) : 보통의 queue와 비슷하나, 각 요소들은 우선순위를 가지고 우선순위 값에 따라 요소를 정렬하는 queue 유형입니다. 더 높은 우선순위를 가지는 요소가 더 낮은 우선순위를 가진 요소보다 먼저 처리됩니다.
-
우선순위가 동일한 경우, queue 특징에 따라 순서에 따라 처리됩니다.
-
배열(Array), 연결 리스트(Linked-List), 힙(Heap), 이진 검색 트리(Binary Search Tree)로도 구현이 가능하고, 각 방법마다 장·단점을 가집니다.
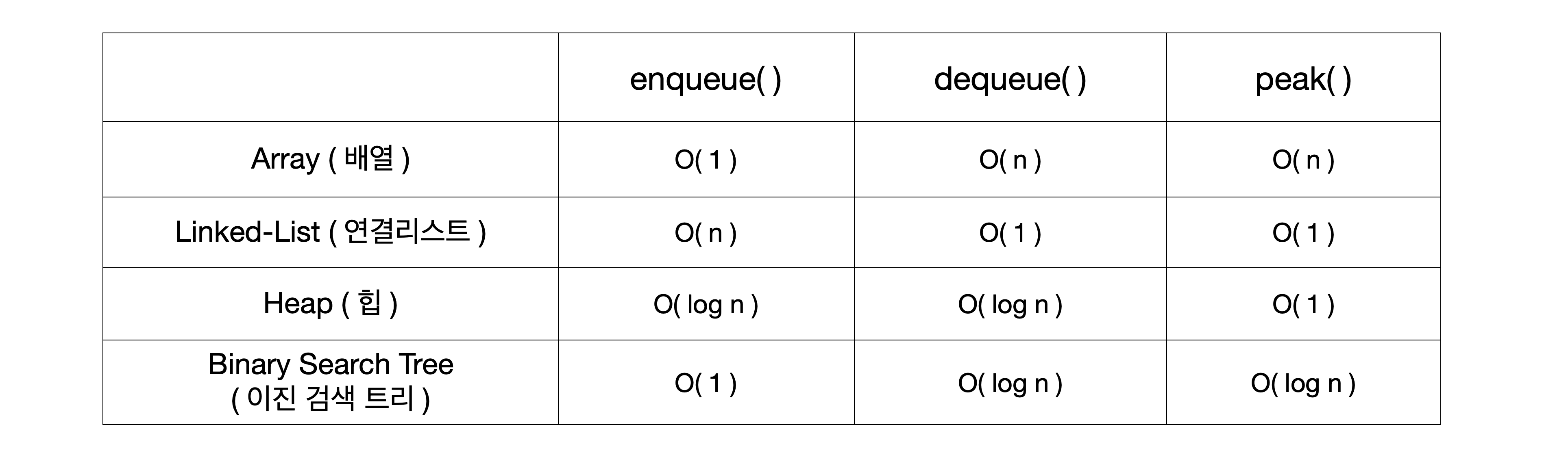
배열 혹은 리스트로 구현하는 경우 삽입 순으로 저장하고 요소를 제거하거나 다음 요소를 반환해야할 때 리스트 전체를 순회하면서 우선순위를 비교합니다. 이는 매우 비효율적입니다. 매번 모든 리스트를 순회하며 전부 비교하므로O(n)의 시간복잡도를 가집니다. -
힙으로 구현하는 경우가 다른 경우보다 삽입과 삭제에서 효율적이므로 이 글에서는 힙으로 구현하는 우선순위 큐에 대해 설명할 것입니다. 이렇듯 우선순위 큐를 보통 힙을 사용해 구현하는 경우가 많아 둘을 혼동하곤 하지만 우선순위 큐와 힙은 별개의 개념입니다.
-
대게 숫자가 낮을 수록 우선순위가 높습니다. 즉, 우선순위가 0순위 혹은 1순위일 때 가장 우선됩니다. 따라서 최소 힙으로 구현됩니다.
☀️ characteristic of Priority Queue ( 특징 )
🙆🏻♀️ 장 점
- 힙 구조를 사용하므로 요소에 더 빠른 방법으로 접근할 수 있습니다.
- 우선순위 값을 업데이트할 수 있고, 요소 순서는 재정렬 되면서 동적으로 수행됩니다.
🙅🏻♀️ 단 점
- 어떠한 자료구조로 구현하느냐에 따라 성능과 복잡성이 크게 달라집니다. 또한 우선순위 큐는 원소의 삽입/삭제, 우선순위 변경, 우선순위 요소 추출 등 다양한 연산을 지원하므로 연산이 복잡해질 수 있습니다. 또 다양한 목적으로 사용되므로 사용 목적에 따라서도 복잡성이 높습니다.
- 우선순위 값을 저장하면서 추가 메모리를 차지하므로 메모리 소비가 높은 편입니다.
- 항상 가장 효율적인 데이터 구조는 아니며, 데이터가 동적으로 업데이트 되면서 예측과 관리가 어렵습니다.요
🪴 적 용
- 서로 다른 우선순위를 가지는 데이터나 정보를 관리할필요가 있거나, 입력 순서대로 우선순위를 가지지 않거나, 순서에 맞춰 입력하지 않는 경우 사용됩니다. 👉🏻 응급실 환자치료 순서, Unix process 등..
- 처리 순서가 중요한 결과를 가져오는 실시간 시스템에 자주 사용됩니다.
- 그래프의 최단경로를 찾는 Dijkstra 알고리즘, 경로 찾기 검색 알고리즘 과 같이 효율성을 향상시키기 위한 알고리즘에도 사용됩니다.
☀️ Implement of Priority Queue ( 구현 )
힙에서 구현한 것과 거의 동일하지만, 요소의 값이 아닌 우선순위로 비교하여 heapify를 진행하도록 수정합니다.
👉🏻 Node 생성
- 요소를 추가하는 경우, 힙과 달리 요소 자체를 삽입하는 것이 아니라, 값과 우선순위를 가지고 새 노드를 만들어 추가합니다.
class Node {
constructor(value, priority) {
this.value = value;
this.priority = priority;
}
}👉🏻 Priority Queue 생성
class PriorityQueue {
constructor() {
this.arr = [];
}👉🏻 Enqueue() ( 요소 삽입 )
enqueue(val, priority) {
//위에서 만든 노드 생성 class를 사용해 요소 자체가 아닌 노드를 삽입합니다.
let newNode = new Node(val, priority);
this.arr.push(newNode);
this.bubbleUp();
}
bubbleUp() {
let idx = this.arr.length - 1;
const element = this.arr[idx];
while(idx > 0){
let parentIdx = Math.floor((idx - 1) / 2);
let parent = this.arr[parentIdx];
// 🌟 요소의 값이 아닌 우선순위로 비교합니다. 🌟
if(element.priority >= parent.priority) break;
this.arr[parentIdx] = element;
this.arr[idx] = parent;
idx = parentIdx;
}
}
👉🏻 Dequeue() ( 요소 삭제 )
dequeue() {
const top = this.arr[0];
const end = this.arr.pop();
if(this.arr.length > 0) {
this.arr[0] = end;
this.bubbleDown();
};
return top;
}
bubbleDown(){
let idx = 0;
const length = this.arr.length;
const element = this.arr[0];
while(true){
let leftChildIdx = 2 * idx + 1;
let rightChildIdx = 2 * idx + 2;
let leftChild,rightChild;
let swap = null;
if(leftChildIdx < length){
leftChild = this.arr[leftChildIdx];
//🌟 요소의 값이 아닌 우선순위로 비교합니다. 🌟
if(leftChild.priority < element.priority) {
swap = leftChildIdx;
}
}
if(rightChildIdx < length){
rightChild = this.arr[rightChildIdx];
if(
(swap === null && rightChild.priority < element.priority) ||
(swap !== null && rightChild.priority < leftChild.priority)
) {
swap = rightChildIdx;
}
}
if(swap === null) break;
this.arr[idx] = this.arr[swap];
this.arr[swap] = element;
idx = swap;
}
}
}🌈 Finish
- 우선순위 큐에 대해서 들어본지는 꽤 됐는데, 처음으로 구현을 해보았다. 이름이 우선순위 큐라서 당연히 큐 자료구조를 사용할 줄 알았는데 힙을 사용해서 신기했다. 보통의 큐의 FILO 규칙을 따르지 않고 우선순위에 따라 처리되는 점에서 왜 이름이 이렇게 되었는 지 의문이 생겼다. (위키백과를 통해 우선순위 큐도 평범한 큐나 스택과 비슷한 축약 자료형이라는 부분을 읽고 어느정도 이해가 갔다)
- Array, Linked-List, Binary-Search-Tree를 공부할 때, 해당 자료형으로도 우선순위 큐를 구현해 봐야겠다.
- 구현한 코드를 기반으로 프로그래머스-더 맵게문제를 풀어보았다. 실제로 사용해 보자 잘못 짜인 코드도 발견할 수 있었고, 힙에 대해 조금 더 이해가 되었다. 좀 더 많은 문제를 풀어봐야 겠다.

