[ ᴀʟɢᴏʀɪᴛʜᴍ ] Graph Traversal ( 그래프 순회 ) - BFS & DFS

NewHa·2023년 9월 19일

algorithm

ᴀʟɢᴏʀɪᴛʜᴍ

목록 보기

15/18

그래프(Graph)

그래프는 노드(Node)와 간선(Edge)로 구성된 자료구조입니다. 여러 개의 점이 선으로 연결되어 있는 구조로, 간선에 방향이 있으면 방향 그래프, 방향이 없으면 양방향 그래프라고 합니다.

🔗

그래프에 관한 더 자세한 내용은 다음 게시글을 참고해주세요.

그래프 탐색

그래프 탐색(순회)란 그래프 내의 모든 노드를 한 번씩 방문하여 살펴보는 것을 말합니다.

현실 세계의 많은 것들을 그래프 형태로 표현할 수 있습니다. 가장 쉽게 볼 수 있는 예가 ‘지하철 노선도’입니다. 각각의 역들(Node)이 간선으로 이어져있습니다. 우리는 도착지까지 최단 거리, 최소 환승 등에 따라 경로를 찾습니다. 이 때 그래프 탐색을 사용해서 경로를 찾을 수 있습니다.

그래프 탐색 알고리즘으로는 깊이 우선 탐색(DFS)과 너비 우선 탐색(BFS), 두 가지 방식이 존재합니다. 두 알고리즘 모두 모든 노드를 방문하므로 시간복잡도는 O(노드수 + 간선수)입니다.

일반적인 그래프 탐색 문제에서는 깊이 우선 탐색과 너비 우선 탐색 모두 사용 가능합니다. 만약 문제가 시작 노드로부터 가까운 노드 순으로 방문해야 하는 경우에는 너비 우선 탐색으로 구현해야합니다.

그래프 탐색은 차후 다익스트라 알고리즘, 크루스칼/프림 알고리즘, 위상 정렬과 같은 다른 알고리즘의 기반이 됩니다.

깊이 우선 탐색(DFS, Depth-First Search)

DFS는 한 방향으로 갈 수 있을 때까지 깊게 내려갔다가, 더 이상 갈 곳이 없으면 돌아와서 다른 방향을 탐색하는 방식의 그래프 탐색 알고리즘입니다. 즉 현재 탐색 중인 노드를 기준으로 해당 노드에 연결된 노드들을 타고 최대한 쭉 내려가서, 깊이를 우선으로 탐색하여 깊이 우선 탐색이라고 부릅니다.

DFS는 예를 들면 미로 길찾기와 같습니다. 갈 수 있는 곳을 따라 계속 앞으로 전진하다가 벽을 만나면 다시 되돌아와서 다른 갈래의 길로 다시 전진하는 것과 같습니다. 그러한 과정을 반복하며 모든 길을 찾는 것입니다.

아래 예시를 통해 자세하게 알아보겠습니다.

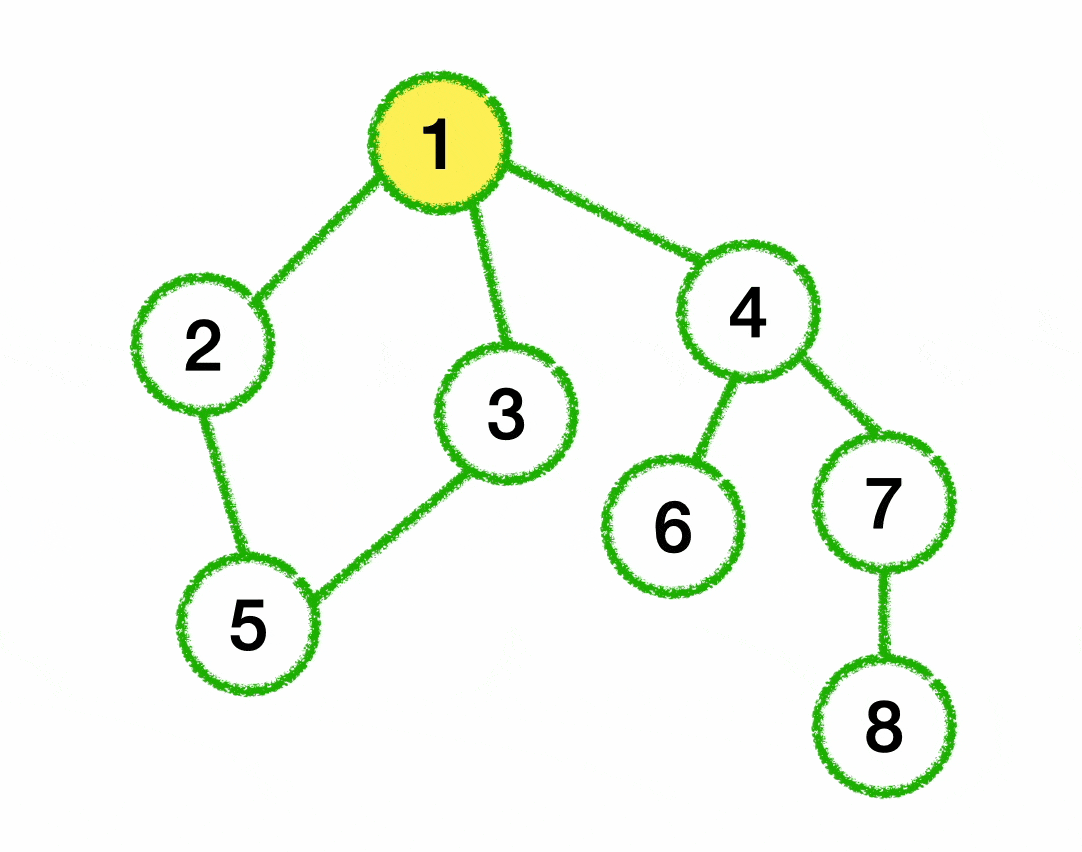
1번 노드를 시작 노드로 합니다. 1번 노드를 방문하고 방문표시를 남깁니다.
- 1번 노드와 연결된 2번 노드를 방문하고 방문표시를 남깁니다.
  - 2번 노드와 연결된 5번 노드를 방문하고 방문표시를 남깁니다.
    - 5번 노드와 연결된 3번 노드르 방문하고 방문표시를 남깁니다.
3번 노드와 연결된 1번 노드를 방문하지만, 방문표시가 되어 있으므로 1과 연결된 다른 간선으로 이동합니다.
- 1번 노드와 연결된 4번 노드를 방문하고 방문표시를 남깁니다.
  - 4번 노드와 연결된 6번 노드를 방문하고 방문표시를 남깁니다.
- 더이상 연결된 노드가 없으므로 4번 노드로 돌아가지만, 방문 표시가 되어 있으므로 4와 연결된 다른 간선을 통해 7번 노드를 방문하고 방문표시를 남깁니다.
  - 7번 노드와 연결된 8번 노드를 방문하고 방문표시를 남깁니다.
더 이상 연결된 노드가 없으므로 백트래킹으로 되돌아가서 시작 노드인 1번 노드로 돌아가지만 다른 갈래가 없으므로 탐색을 종료합니다.

만약 예시와 다르게 연결되지 않은 그래프라면 모든 정점에 대해 DFS를 한 번씩 호출해서 모든 노드를 탐색해야합니다.

정리하자면, DFS는 다음 원리에 따라 구현합니다.

시작 노드를 방문하고, 이미 방문한 노드는 다시 방문하지 않도록 방문처리를 합니다.
연결된 노드 중 아직 방문하지 않은 노드를 재귀적으로 방문합니다.
더 이상 방문할 노드가 없으면 이전 단게로 돌아가 다른 갈래를 탐색합니다. 이를 백트래킹(backtracking)이라하고 DFS의 핵심 동작 원리입니다.
이러한 과정을 반복해 그래프 전체를 탐색합니다.

1️⃣ 재귀를 이용한 DFS 구현 코드

가장 일반적이고 직관적인 방법입니다. 현재 노드를 방문하고 방문목록에 표시하고, 연결된 노드를 재귀함수로 호출해서 탐색합니다.

// 예시의 그래프는 다음과 같습니다.
const graph = {
  1: [2, 3, 4],
  2: [1, 5],
  3: [1, 5],
  4: [1, 6],
  5: [2, 3],
  6: [4, 7],
  7: [6, 8],
  8: [7],
};

const visited = new Set();

// 시작 노드를 정해줍니다.
function DFS(start){
	// 방문목록에 있는 node면 종료합니다.
	if(visited.has(start)) return;
	// 아니라면 해당 노드를 출력하고 방문목록에 추가합니다.
	console.log(start);
	visited.add(start);
	
	// 해당 노드에 연결된 노드를 순회하면서
	for(const next of graph[start]) {
		// 방문 목록에 없는 노드라면
		if(!visitied.has(next) {
			// 재귀적으로 DFS를 호출합니다.
			DFS(next)
		}
	}
}

DFS(1); // 1 → 2 → 5 → 3 → 4 → 6 → 7 → 8 순으로 출력됩니다.

2️⃣ 스택을 이용한 DFS 구현 코드

재귀 대신 스택을 사용하여 반복문으로도 구현할 수 있습니다. Node.js에서는 재귀적으로 DFS를 호출하는 경우 stack overflow로 에러가 발생할 수 있습니다. 이 때, 스택을 사용해서 이를 방지할 수 있습니다.

하지만, 상대적으로 구현이 복잡하고 순서를 제어해야 합니다.

const visited = new Set();

function DFS(start) {
	// 시작 노드를 스택에 추가합니다.
	const stack = [start];
	
	while(stack.length > 0) {
		// 가장 마지막에 넣은 노드를 꺼냅니다.
		const node = stack.pop();
	
		// 방문목록에 없는 노드라면 출력하고 방문목록에 추가합니다.
		if(!visited.has(node)) {
			console.log(node);
			visited.add(node);
			
			// 연결된 노드를 택에 넣고 역순으로 push합니다.
			for(let i = graph[node].length - 1; i >= 0; i--) {
				const next = graph[node][i];
				if(!visited.has(node)) {
					stack.push(next)
				}
			}
		}
	}
}

DFS(1); // 1 → 2 → 5 → 3 → 4 → 6 → 7 → 8 순으로 출력됩니다.

너비 우선 탐색(BFS, Breadth-First Search)

BFS는 시작 노드를 기준으로 거리가 가까운 노드부터 하나씩 넓게 탐색하는 방식의 그래프 탐색 알고리즘입니다. 큐(Queue)를 사용해 현재 위치에서 인접한 모든 노드를 먼저 탐색한 후, 그 다음 깊이로 진행합니다.

같은 그래프 예시를 통해 알아보겠습니다.

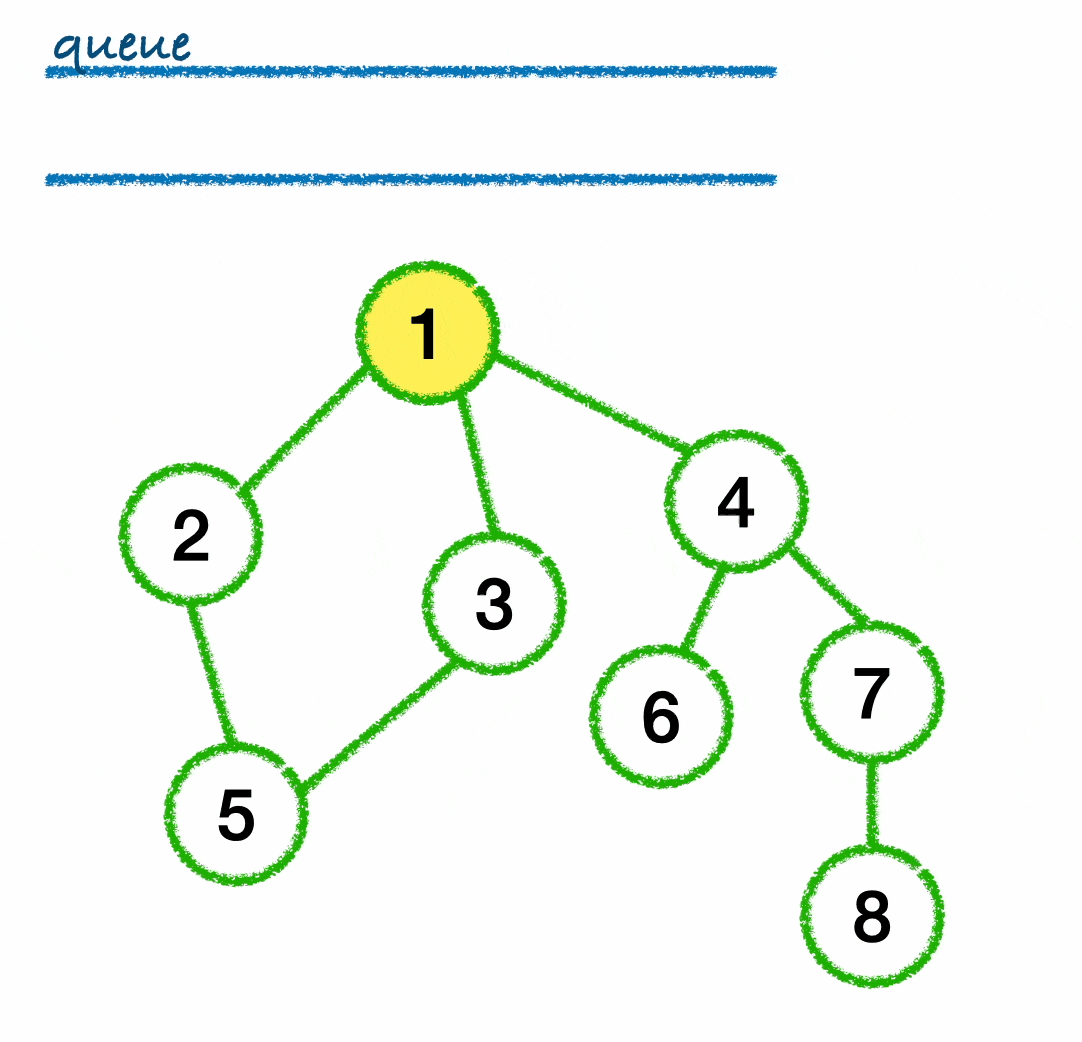
1번 노드를 시작노드로 합니다. 1번 노드를 큐에 넣고 방문표시를 합니다.
큐에서 1번 노드를 꺼냅니다.
- 1번 노드와 연결된 2번 노드를 방문하고 방문표시가 없으므로 2번 노드를 큐에 넣고 방문표시를 합니다.
- 1번 노드와 연결된 3번 노드를 방문하고 방문표시가 없으므로 3번 노드를 큐에 넣고 방문표시를 합니다.
- 1번 노드와 연결된 4번 노드를 방문하고 방문표시가 없으므로 4번 노드를 큐에 넣고 방문표시를 합니다.
더이상 1번 노드에 연결된 노드가 없으므로 큐에서 다음 노드인 2번 노드를 꺼냅니다.
- 2번 노드와 연결된 1번 노드를 방문합니다. 방문 표시가 있으므로 넘어갑니다.
- 2번 노드와 연결된 5번 노드를 방문합니다. 방문표시가 없으므로 5번 노드를 큐에 넣고 방문표시를 합니다.
더 이상 2번 노드에 연결된 노드가 없으므로 큐에서 다음 노드인 3번 노드를 꺼냅니다.
- 3번 노드와 연결된 1번 노드를 방문합니다. 방문 표시가 있으므로 넘어갑니다.
- 3번 노드와 연결된 5번 노드를 방문합니다. 방문 표시가 있으므로 넘어갑니다.
더 이상 3번 노드에 연결된 노드가 없으므로 큐에서 다음 노드인 4번 노드를 꺼냅니다.
- 4번 노드와 연결된 1번 노드를 방문합니다. 방문 표시가 있으므로 넘어갑니다.
- 4번 노드와 연결된 6번 노드를 방문합니다. 방문표시가 없으므로 6번 노드를 큐에 넣고 방문표시를 합니다.
- 4번 노드와 연결된 7번 노드를 방문합니다. 방문표시가 없으므로 7번 노드를 큐에 넣고 방문표시를 합니다.
더 이상 4번 노드에 연결된 노드가 없으므로 큐에서 다음 노드인 5번 노드를 꺼냅니다.
- 5번 노드와 연결된 2번 노드를 방문합니다. 방문 표시가 있으므로 넘어갑니다.
- 5번 노드와 연결된 3번 노드를 방문합니다. 방문 표시가 있으므로 넘어갑니다.
더이상 5번 노드에 연결된 노드가 없으므로 큐에서 다음 노드인 6번 노드를 꺼냅니다.
- 6번 노드와 연결된 4번 노드를 방문합니다. 방문 표시가 있으므로 넘어갑니다.
더이상 6번 노드에 연결된 노드가 없으므로 큐에서 다음 노드인 7번 노드를 꺼냅니다.
- 7번 노드와 연결된 4번 노드를 방문합니다. 방문 표시가 있으므로 넘어갑니다.
- 7번 노드와 연결된 8번 노드를 방문합니다. 방문표시가 없으므로 8번 노드를 큐에 넣고 방문표시를 합니다.
더이상 7번 노드에 연결된 노드가 없으므로 큐에서 다음 노드인 8번 노드를 꺼냅니다.
- 8번 노드와 연결된 7번 노드를 방문합니다. 방문 표시가 있으므로 넘어값니다.
탐색을 종료합니다.

정리하자면 BFS는 다음 원리에 따라 구현합니다.

시작 노드를 큐에 넣고 방문처리합니다.
큐에서 노드를 하나씩 꺼내어 그 노드와 연결된 모든 노드를 큐에 추가하고 방문처리 합니다.
큐가 빌 때까지 반복하여 탐색합니다.

🚀 BFS 구현 코드

const visited = new Set();

function BFS(start) {
	// 큐에 시작 노드를 넣어주고, 방문표시를 합니다.
	const queue = [start];
	visited.add(start);
	
	// 큐가 빌 때까지 반복합니다.
	while(queue.length > 0) {
		// 큐에서 노드를 꺼내어 출력합니다.
		const node = queue.shift();
		console.log(node);
		
		// 해당 노드에 연결된 노드를 순회합니다.
		for(const next of graph[node]){
			// 연결된 노드가 방문목록에 없으면 큐에 추가하고 방문표시를 합니다.
			if(!visited.has(next)) {
				queue.push(next);
				visited.add(next);
			}
		}
	}
}

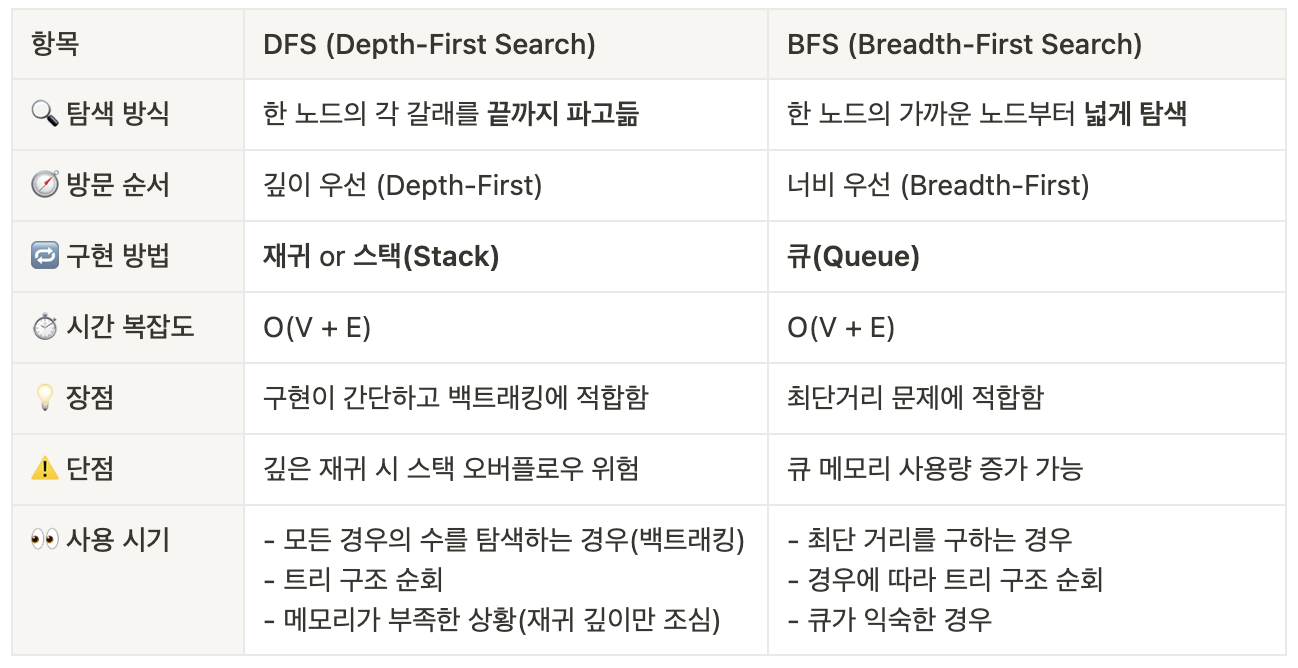
BFS(1); // 1 → 2 → 3 → 4 → 5 → 6 → 7 → 8 순으로 출력됩니다.

DFS vs BFS 비교 정리

백준 2468번 문제

🌐 백준 2468번 - 안전 영역

재난방재청에서는 많은 비가 내리는 장마철에 대비해서 다음과 같은 일을 계획하고 있다. 먼저 어떤 지역의 높이 정보를 파악한다. 그 다음에 그 지역에 많은 비가 내렸을 때 물에 잠기지 않는 안전한 영역이 최대로 몇 개가 만들어 지는 지를 조사하려고 한다. 이때, 문제를 간단하게 하기 위하여, 장마철에 내리는 비의 양에 따라 일정한 높이 이하의 모든 지점은 물에 잠긴다고 가정한다.

어떤 지역의 높이 정보는 행과 열의 크기가 각각 N인 2차원 배열 형태로 주어지며 배열의 각 원소는 해당 지점의 높이를 표시하는 자연수이다. 예를 들어, 다음은 N=5인 지역의 높이 정보이다.

많은 비가 내려서 높이가 4 이하인 모든 지점이 물에 잠겼다고 하자. 이 경우에 물에 잠기는 지점을 회색으로 표시하면 다음과 같다. 물에 잠기지 않는 안전한 영역이라 함은 물에 잠기지 않는 지점들이 위, 아래, 오른쪽 혹은 왼쪽으로 인접해 있으며 그 크기가 최대인 영역을 말한다. 위의 경우에서 물에 잠기지 않는 안전한 영역은 5개가 된다(꼭짓점으로만 붙어 있는 두 지점은 인접하지 않는다고 취급한다).

장마철에 내리는 비의 양에 따라서 물에 잠기지 않는 안전한 영역의 개수는 다르게 된다. 위의 예와 같은 지역에서 내리는 비의 양에 따른 모든 경우를 다 조사해 보면 물에 잠기지 않는 안전한 영역의 개수 중에서 최대인 경우는 5임을 알 수 있다.

어떤 지역의 높이 정보가 주어졌을 때, 장마철에 물에 잠기지 않는 안전한 영역의 최대 개수를 계산하는 프로그램을 작성하시오.

입력

첫째 줄에는 어떤 지역을 나타내는 2차원 배열의 행과 열의 개수를 나타내는 수 N이 입력된다. N은 2 이상 100 이하의 정수이다. 둘째 줄부터 N개의 각 줄에는 2차원 배열의 첫 번째 행부터 N번째 행까지 순서대로 한 행씩 높이 정보가 입력된다. 각 줄에는 각 행의 첫 번째 열부터 N번째 열까지 N개의 높이 정보를 나타내는 자연수가 빈 칸을 사이에 두고 입력된다. 높이는 1이상 100 이하의 정수이다.

출력

첫째 줄에 장마철에 물에 잠기지 않는 안전한 영역의 최대 개수를 출력한다.

문제풀이

❗

자바스크립트는 파이썬에 비해 재귀 호출 깊이의 제한이 더 낮아서 DFS로 푸는 경우 stack overflow로 런타임 에러가 날 수 있습니다. 자바스크립트로 푸는 경우 BFS가 더 안전합니다.

(실제로, 최고 높이(h)를 구해 반복문을 제한하지 않고, 입력 조건에 따라 최대값인 100까지 구하려고 하면 DFS는 런타임 에러가 납니다. BFS는 100까지 구하더라도 통과합니다.)

🚀 DFS로 구현한 코드

한 칸에서 시작해, 인접한 안전한 칸들을 재귀적으로 모두 방문합니다. 하나의 영역을 재귀 호출로 모두 탐색 후 영역 개수(count)를 +1 합니다.

const fs = require('fs');
const input = fs.readFileSync('/dev/stdin').toString().trim().split('\n');

// 첫 번째 줄은 N (지도 크기)
const N = +input[0];
// 이후 N줄은 지도의 높이 정보 (2차원 배열로 변환)
const landMap = input.slice(1).map(line => line.split(' ').map(Number));

// 상하좌우 탐색을 위한 방향 벡터
const dx = [0, 1, 0, -1]; // → ↓ ← ↑ (행 이동)
const dy = [-1, 0, 1, 0]; // → ↓ ← ↑ (열 이동)

// 방문 여부를 저장할 2차원 배열 (전역으로 선언해 사용)
let visited;

// 깊이 우선 탐색 (DFS) 함수 정의
const dfs = (x, y, h) => {
    // 현재 위치 방문 표시
    visited[x][y] = true;

    // 4방향으로 탐색
    for (let i = 0; i < 4; i++) {
        const nextX = x + dx[i]; // 다음 x 좌표
        const nextY = y + dy[i]; // 다음 y 좌표

        // 범위 안에 있고, 방문하지 않았고, 물에 잠기지 않은 경우
        if (
            nextX >= 0 && nextX < N &&
            nextY >= 0 && nextY < N &&
            !visited[nextX][nextY] &&
            landMap[nextX][nextY] > h // 비 높이보다 높은 땅이면 안전 영역
        ) {
            dfs(nextX, nextY, h); // 다음 위치로 DFS 호출
        }
    }
};

// 특정 높이 h에서 안전 영역 개수를 구하는 함수
const getCount = (h) => {
    // visited 배열 초기화 (false로 설정)
    visited = Array.from({ length: N }, () => Array(N).fill(false));

    let count = 0; // 안전 영역 개수

    // 전체 좌표를 순회
    for (let x = 0; x < N; x++) {
        for (let y = 0; y < N; y++) {
            // 방문하지 않았고, 물에 잠기지 않은 경우 → 새로운 영역 시작
            if (!visited[x][y] && landMap[x][y] > h) {
                dfs(x, y, h); // DFS로 연결된 안전 영역 탐색
                count++;      // 안전 영역 1개 증가
            }
        }
    }
    return count; // 안전 영역 개수 반환
};

// 지도에서 가장 높은 높이를 구함 (최대 비 높이 설정용)
let maxHeight = 0;
for (let x = 0; x < N; x++) {
    for (let y = 0; y < N; y++) {
        maxHeight = Math.max(maxHeight, landMap[x][y]);
    }
}

// 정답 변수 (최대 안전 영역 개수)
let result = 0;

// 비의 높이를 0부터 최대 높이까지 바꿔가며 안전 영역 개수 탐색
for (let h = 0; h <= maxHeight; h++) {
    result = Math.max(result, getCount(h)); // 최대값 갱신
}

// 결과 출력
console.log(result);

🚀 BFS로 구현한 코드

한 칸에서 시작해, 큐를 이용해 인접한 칸들을 하나씩 방문합니다. 하나의 영역을 큐가 빌 때까지 모두 탐색하고 영역 개수(count)를 +1 합니다.

const fs = require('fs');
const input = fs.readFileSync('/dev/stdin').toString().trim().split('\n');

// 첫 번째 줄에서 지도의 크기 N을 추출
const N = +input[0];
// N개의 줄을 2차원 숫자 배열로 변환 → landMap이라는 변수에 저장
const landMap = input.slice(1).map(line => line.split(' ').map(Number));

// 상하좌우 방향을 나타내는 배열 (dy: y축 이동, dx: x축 이동)
const dx = [0, 1, 0, -1];
const dy = [-1, 0, 1, 0];

// 방문 여부를 체크하는 2차원 배열 (전역으로 선언)
let visited;

/**
 * 너비 우선 탐색(BFS)
 * - 현재 좌표 (x, y)에서 시작하여 연결된 안전 영역을 모두 방문 처리
 * - 비의 높이 h보다 높은 땅만 탐색
 */
const bfs = (x, y, h) => {
    const q = []; // 큐 생성
    visited[x][y] = true; // 시작 지점 방문 표시
    q.push([x, y]); // 시작 지점을 큐에 넣음

    while (q.length > 0) {
        const [x, y] = q.shift(); // 큐에서 하나 꺼냄

        // 상하좌우로 이동
        for (let i = 0; i < 4; i++) {
            const nextX = x + dx[i]; // 다음 x 위치
            const nextY = y + dy[i]; // 다음 y 위치

            // 다음 위치가 범위 안에 있고, 방문하지 않았으며, 물에 잠기지 않은 경우
            if (
                nextX >= 0 && nextX < N &&
                nextY >= 0 && nextY < N &&
                !visited[nextX][nextY] &&
                landMap[nextX][nextY] > h
            ) {
                visited[nextX][nextY] = true; // 방문 처리
                q.push([nextX, nextY]); // 큐에 다음 위치 추가
            }
        }
    }
};

/**
 * 특정 비의 높이(h)일 때 안전 영역의 개수를 구하는 함수
 */
const getCount = (h) => {
    // visited 배열을 false로 초기화 (N x N 크기)
    visited = Array.from({ length: N }, () => Array(N).fill(false));

    let count = 0; // 안전 영역 개수 초기화

    // 모든 좌표를 순회하며 탐색
    for (let x = 0; x < N; x++) {
        for (let y = 0; y < N; y++) {
            // 방문하지 않았고, 현재 위치가 물에 잠기지 않았다면
            if (!visited[x][y] && landMap[x][y] > h) {
                bfs(x, y, h); // bfs로 연결된 영역 전체 방문 처리
                count++; // 안전 영역 개수 +1
            }
        }
    }

    return count; // 해당 높이에서의 안전 영역 개수 반환
};

// landMap 내에서 가장 높은 지형의 높이를 구함 (비의 최대 높이 설정용)
let maxHeight = 0;
for (let x = 0; x < N; x++) {
    for (let y = 0; y < N; y++) {
        maxHeight = Math.max(maxHeight, landMap[x][y]);
    }
}

// 안전 영역 개수 중 최대값을 저장할 변수
let result = 0;

// 비의 높이를 0부터 maxHeight까지 증가시키며 모든 경우를 탐색
for (let h = 0; h <= maxHeight; h++) {
    result = Math.max(result, getCount(h)); // 안전 영역의 최대 개수 갱신
}

// 최종 결과 출력
console.log(result);

NewHa

백 번을 보면 한 가지는 안다 👀

이전 포스트

[ ᴀʟɢᴏʀɪᴛʜᴍ ] Graph Data Structure( 그래프 )

다음 포스트

[ ᴀʟɢᴏʀɪᴛʜᴍ ] Graph Traversal ( 그래프 순회 ) - BFS & DFS