[ ᴀʟɢᴏʀɪᴛʜᴍ ] Bubble Sort ( 버블 정렬 )

NewHa·2023년 9월 7일

ᴀʟɢᴏʀɪᴛʜᴍ

목록 보기

2/14

🐾 정렬은 어디에 쓰일까? (정렬을 배워야 하는 이유)

우리가 일상 생활에서 사용하는 소프트웨어 대부분에는 정렬이 포함되어 있습니다. e-mail을 확인하러 들어가면 도착 시간 순서대로 정렬이 되어 있고, google에 검색어를 입력해 검색을 하면 검색어와 관련된 순서대로 정렬되어 나타납니다. 이는 곧 개발하는 애플리케이션에서 부딫히는 많은 문제에서 쓰인다는 것입니다.
👉🏻 수많은 데이터 중에서 중요하고 유용한 데이터를 사용자에게 보여주기 위해 정렬을 알아야 합니다.

🌱 Bubble Sort ( 버블 정렬 )

👉🏻 버블 정렬 (整列, bubble sort) : 서로 인접한 두 요소의 크기를 비교하여 순서가 잘못된 경우, 반복적으로 교체하여 정렬하는 알고리즘 입니다. 요소의 이동이 거품이 수면으로 올라오는 듯한 모습을 보이기 때문에 지어진 이름입니다. 정렬 알고리즘 중에서 이해가 가장 쉽고, 간단하고 구현이 쉽습니다.

인접한 두 요소의 상대적 순서를 결정하기 위해 비교연산자를 사용하는 비교 기반 정렬 알고리즘 입니다.
비교 하여 두 요소의 위치가 잘못되었다면 두 요소를 교체하는 교환 기반 알고리즘 입니다.
동일한 key값을 가지는 요소는 정렬된 출력에서 상대적인 순서를 유지하므로 안정적인 정렬 알고리즘입니다.

☀️ Operations of Bubble Sort ( 작동 )

왼쪽에서부터 탐색을 시작합니다.

인접한 두 요소를 비교하고 순서가 맞지 않다면 요소를 교체합니다. 1회전 정렬 시마다 가장 크거나 작은 자료가 맨 오른쪽으로 이동하고, 다음 회전에는 정렬된 마지막 자료는 제외합니다. 배열에 아무런 변화가 없을 때까지 회전을 반복합니다.

인접한 요소끼리 비교하므로, 특정 요소가 이미 최종 위치에 있더라도 회전시에 자리가 교체되며, 교체과정이 이동과정보다 복잡해 거의 쓰이지 않습니다. 대규모 데이터 셋에는 부적합한 정렬입니다.

다음은 오름차순을 기준으로 배열을 1회전 정렬하는 모습을 그린 것입니다.

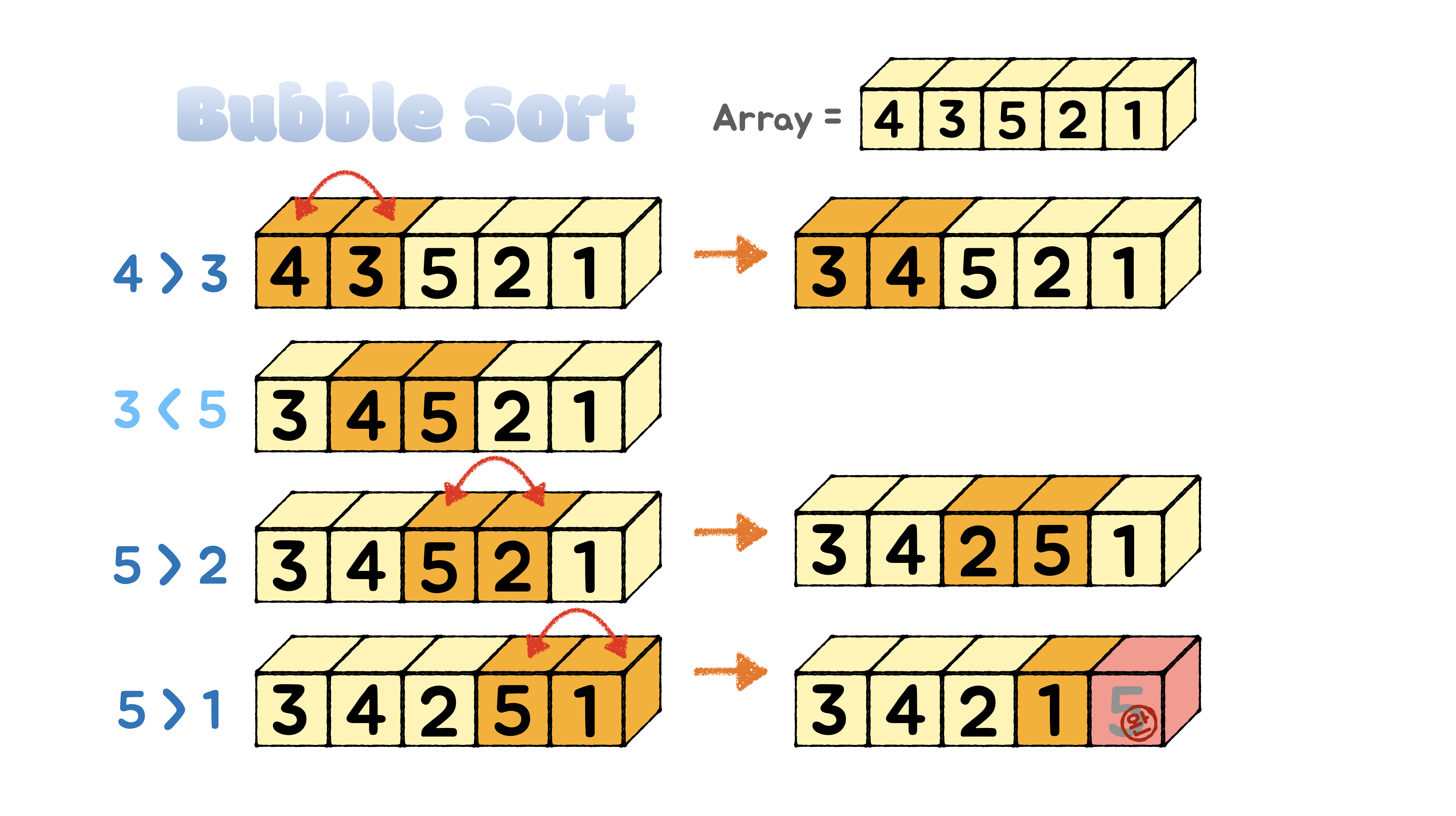
[4, 3, 5, 2, 1]이라는 배열이 주어졌을 때, 우선 가장 왼쪽의 요소와 인접한 요소끼리 비교를 합니다.
4 > 3 으로 왼쪽 요소(4)가 더 크니 위치를 교체해줍니다. ➡️ [3, 4, 5, 2, 1]
그 다음으로 3 < 5를 비교했을 때 오른쪽 요소(5)가 더 크므로 그대로 다음으로 넘어갑니다.
다음 5 > 2로 왼쪽요소(5)가 더 크니 위치를 교체해줍니다. ➡️ [3, 4, 2, 5, 1]
마지막으로 5 > 1을 비교해 더 큰 왼쪽요소(5)를 오른쪽으로 보내주면 맨 오른쪽에 가장 큰 수인 5가 정렬됩니다. ➡️ [3, 4, 2, 1, 5]
이 후 맨 마지막 요소(5)를 제외 하고 비교, 교체 과정을 반복하여 정렬합니다.

☀️ Implementation of Bubble Sort ( 구현 )

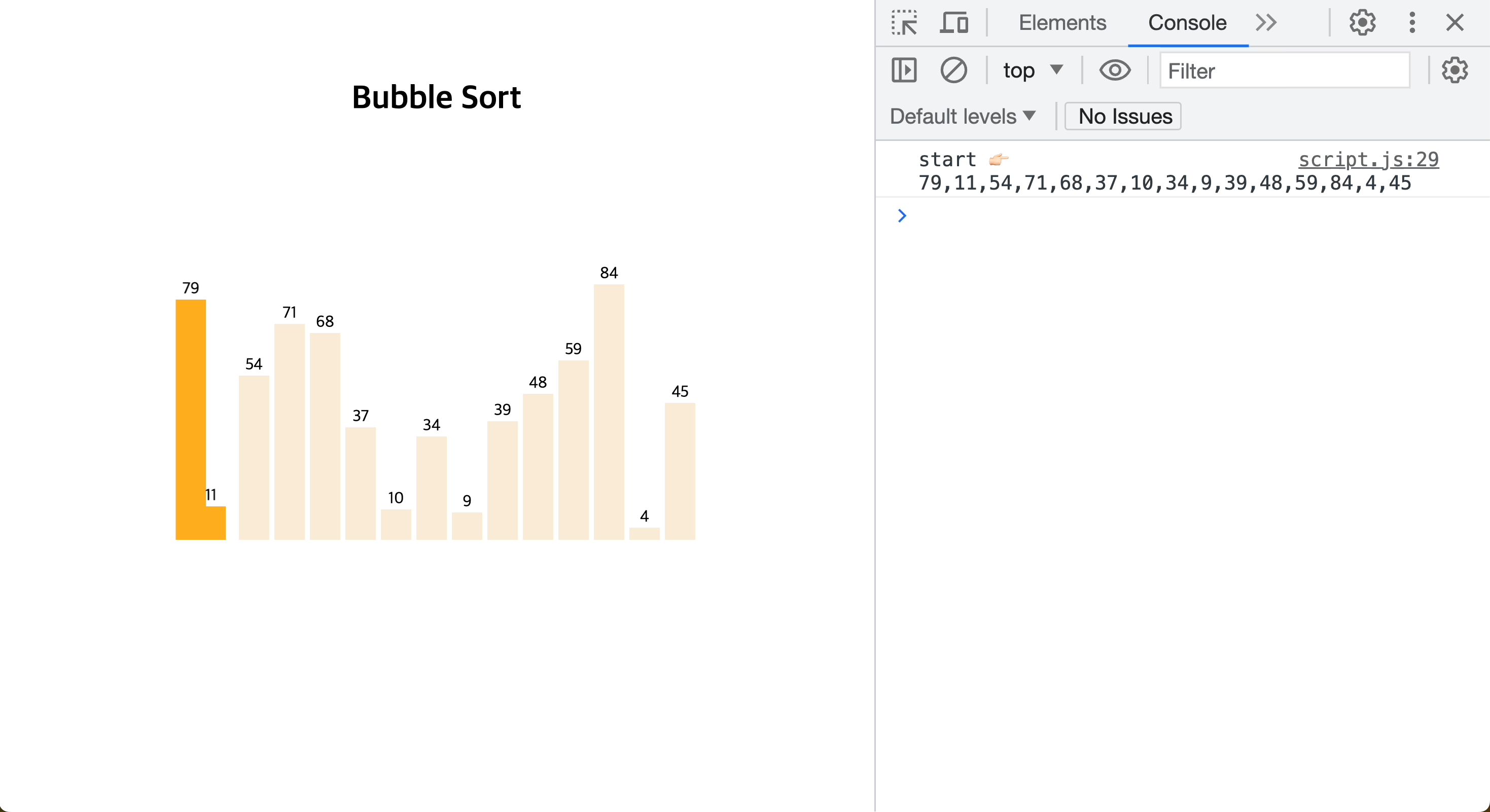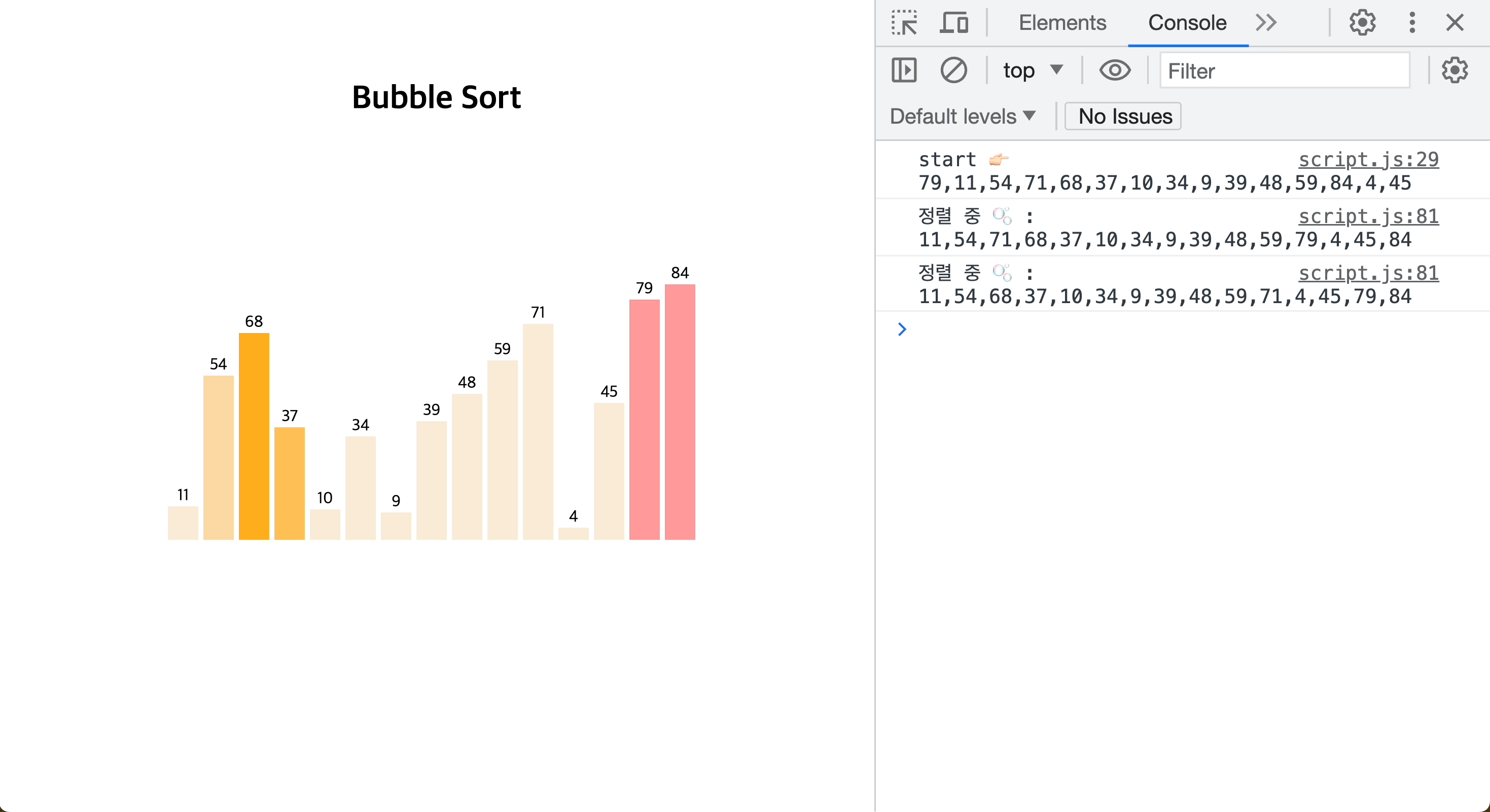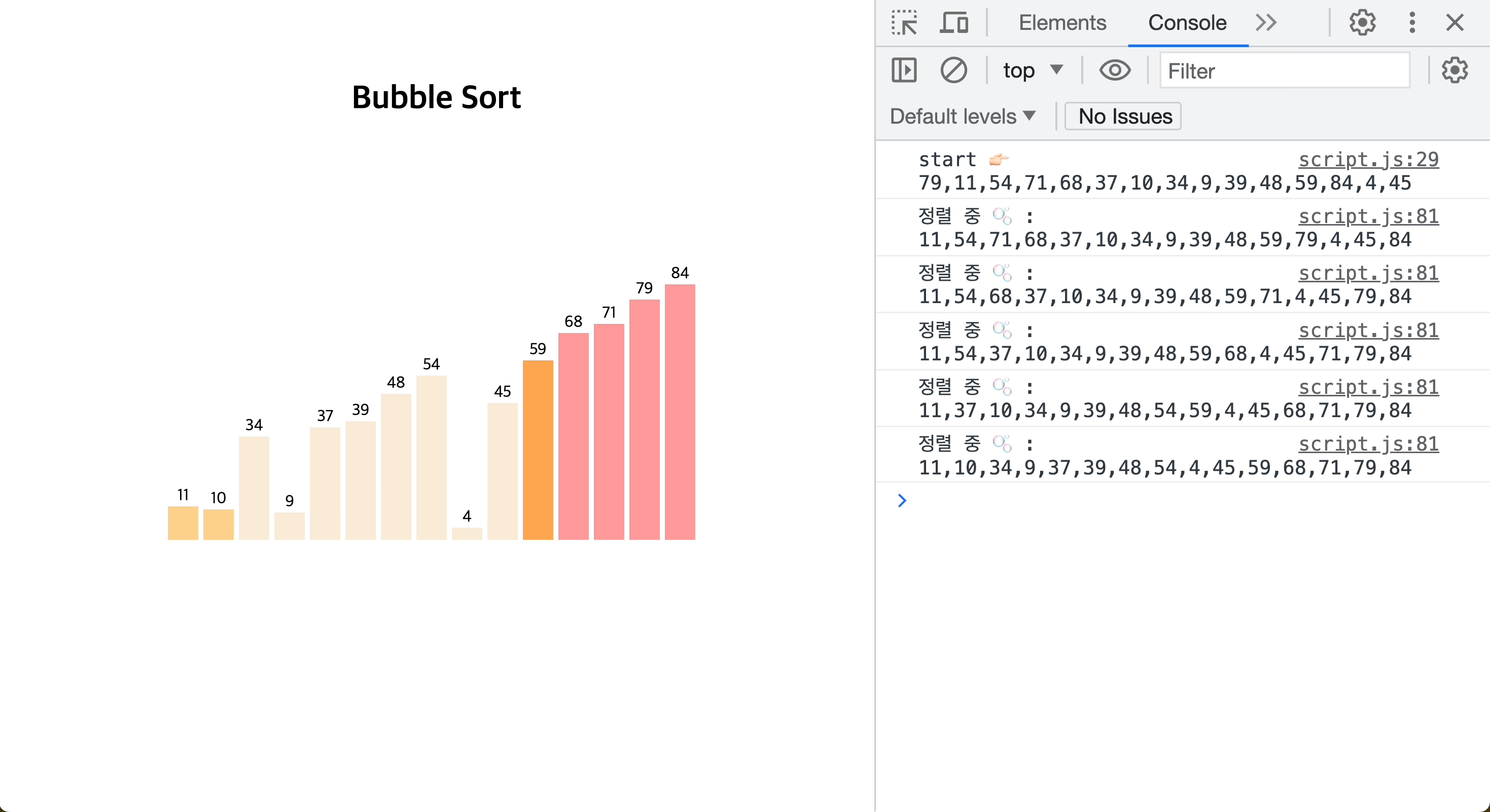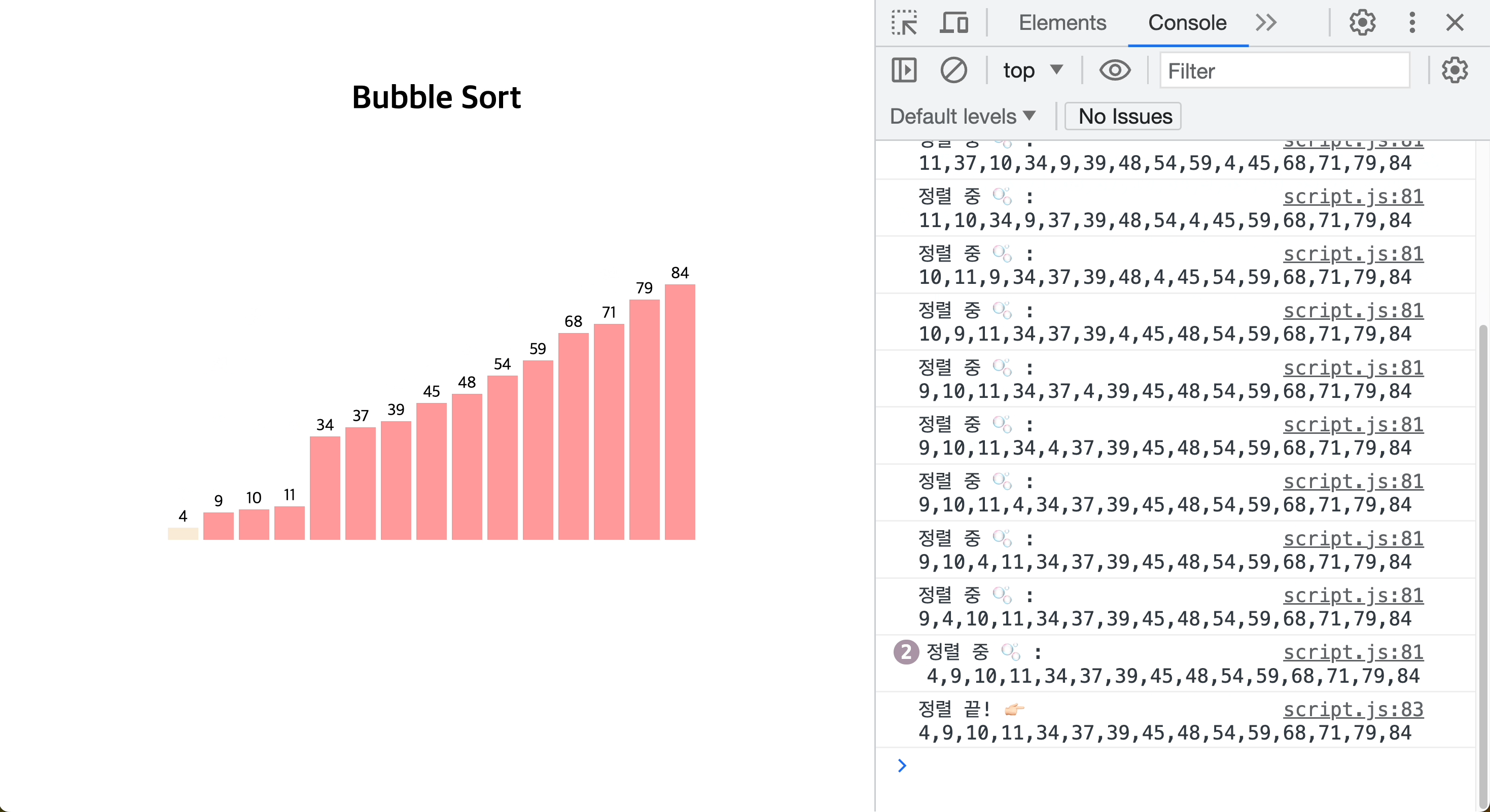
[JavaScript로 버블 정렬하는 모습을 시각화 👉🏻 GitHub repository]

🌿 Basic Implementation (기본 구현)

기본적으로 오름차순을 기준 (arr[j] > arr[j + 1])으로 코드를 작성했으며, 내림차순으로 정렬하려면 이중 for문 안에 if 조건문의 조건에서 arr[j] < arr[j + 1]로 조건을 작성하면 됩니다.

👉🏻 Python으로 구현

def bubbleSort(arr):
	for i in range(len(arr)-1):
    	for j in range(len(arr)-i -1):
        	# 오름차순 기준
        	if arr[j] > arr[j + 1]:
            	# 교체
            	arr[j], arr[j + 1] = arr[j + 1], arr[j];
    return arr

👉🏻 JavaScript로 구현


function bubbleSort(arr) {
  for (let i = 0; i < arr.length -1; i++) {
    for (let j = 0; j < arr.length -i -1; j++) {
      if (arr[j] > arr[j + 1]) {
        [arr[j], arr[j + 1]] = [arr[j + 1], arr[j]];
      }
    }
  }
  return arr
}

👉🏻 Optimization (최적화)

어느 정도 정렬 된 상태거나 진행 중 정렬이 완료된 상태일 경우, 불필요한 연산을 멈춰 성능을 개선할 수 있습니다.

# 최적화한 python 코드
def bubbleSort(arr):
	for i in range(len(arr) -1):
    	isQuit = True;
    	for j in range(len(arr) -i -1):
        	if arr[j] > arr[j + 1]:
            	arr[j], arr[j + 1] = arr[j + 1], arr[j];
                isQuit = False;
        if isQuit:
        	break;
    return arr

// 최적화한 JavaScript 코드
function bubbleSort(arr) {
  for (let i = 0; i < arr.length -1; i++) {
    let isQuit = true;
    for (let j = 0; j < arr.length -i -1; j++) {
      if (arr[j] > arr[j + 1]) {
        [arr[j], arr[j + 1]] = [arr[j + 1], arr[j]];
        isQuit = false;
      }
    }
    if (isQuit) break;
  }
  return arr
}

🌿 Recursive Implemente (재귀적 구현)

버블 정렬을 재귀적으로도 구현할 수 있습니다. 성능이나 구현 상 이점이 있는 것은 아니지만 정렬과 재귀를 이해하는 데 도움이 됩니다.

비교 횟수 기준 재귀적 버블 정렬이 우수하나, 시간복잡도는 동일하게 O(n^2) 입니다.

그러나 공간복잡도 기준으로 재귀적 버블 정렬은 O(n)의 공간복잡도를 가지고, 일반 버블 정렬은 O(1)의 공간복잡도를 가집니다.
function bubbleSort(arr, n) {
	// Base case : 배열의 크기가 1이면 return 한다.
	if (n == 1) return;
  	// 버블정렬을 한 번 실행한다.
	let count = 0;	
	for (let i = 0; i < n - 1; i++) {
		if (arr[i] > arr[i + 1]) {
			[arr[i], arr[i + 1]] = [arr[i + 1], arr[i]];
			count++;
		}
    }
	if (count == 0) return;
  	// recursive : n을 줄여가며 재귀적으로 부른다.
	bubbleSort(arr, n - 1);
}

☀️ Time and Space Complexity Analysis ( 시·공간 복잡도 )

🪴시간복잡도

배열이 이미 정렬되어 있는 최상의 경우, (N - 1)만큼 비교해 O(n)의 복잡도를 가집니다. 반대로 최악의 경우(배열의 요소가 반대로 정렬되어 있는 경우) 필요한 총 반복 횟수는 (N - 1)로 등차수열에 따라 N(N + 1)/2 만큼 반복합니다.즉 O(n^2)의 시간복잡도를 가집니다.
비교횟수가 비교적 일정하여(배열에 관계없이 비교횟수는 동일하기 때문에), 평균적으로 O(n^2)의 시간복잡도를 가져 비효율적인 정렬에 해당합니다.

🪴 공간복잡도

swap 에 사용되는 임시변수 외에 추가 메모리 공간이 필요하지 않기 때문에 O(1)의 공간복잡도를 가집니다. 즉, 추가로 메모리 공간이 필요하지 않는 내부 알고리즘에 해당합니다.

🌈 Finish

처음 개발자 공부를 하겠다고 생각한 계기가 버블 정렬이었다. 어느 유명한 대학에서 한 컴퓨터 공학강의를 보게 되었는데 주제가 '버블정렬'이었다. 8명의 학생들을 줄 세워서 한 명 한 명 차례로 순서를 바꿔가며 정렬하고 컴퓨터로 코드를 쳐서 보여주는데서 너무 재밌어서 시간가는 줄 모르고 봤다. 그 땐 코드 부분에 가서는 저게 뭘까 했던 것 같은데 어느새 내가 구현을 하고 있어서 신기했다.