[ ᴀʟɢᴏʀɪᴛʜᴍ ] Graph Data Structure( 그래프 )

NewHa·2023년 9월 18일
algorithm
1

ᴀʟɢᴏʀɪᴛʜᴍ

목록 보기
13/14
post-thumbnail

🌱 Graph ( 그래프 )


👉🏻 그래프 (graph) : 정점(vertex)으로 부르는 노드들과 두 노드를 연결하는 간선(edge)들의 집합으로 구성된 비선형 데이터 자료 구조를 말합니다. 그래프는 정점을 연결하는 간선이 중요합니다. 연결이 같으면 정점의 내용이 다르더라도 같은 그래프이고, 연결이 다르다면 내용이 같더라도 다른 그래프입니다.

  • 트리 뿐만 아니라, Linked-List, Heaps 자료구조도 제한된 규칙이 적용되는 그래프의 특별한 유형에 속합니다.

    🌿 Graph vs. Tree

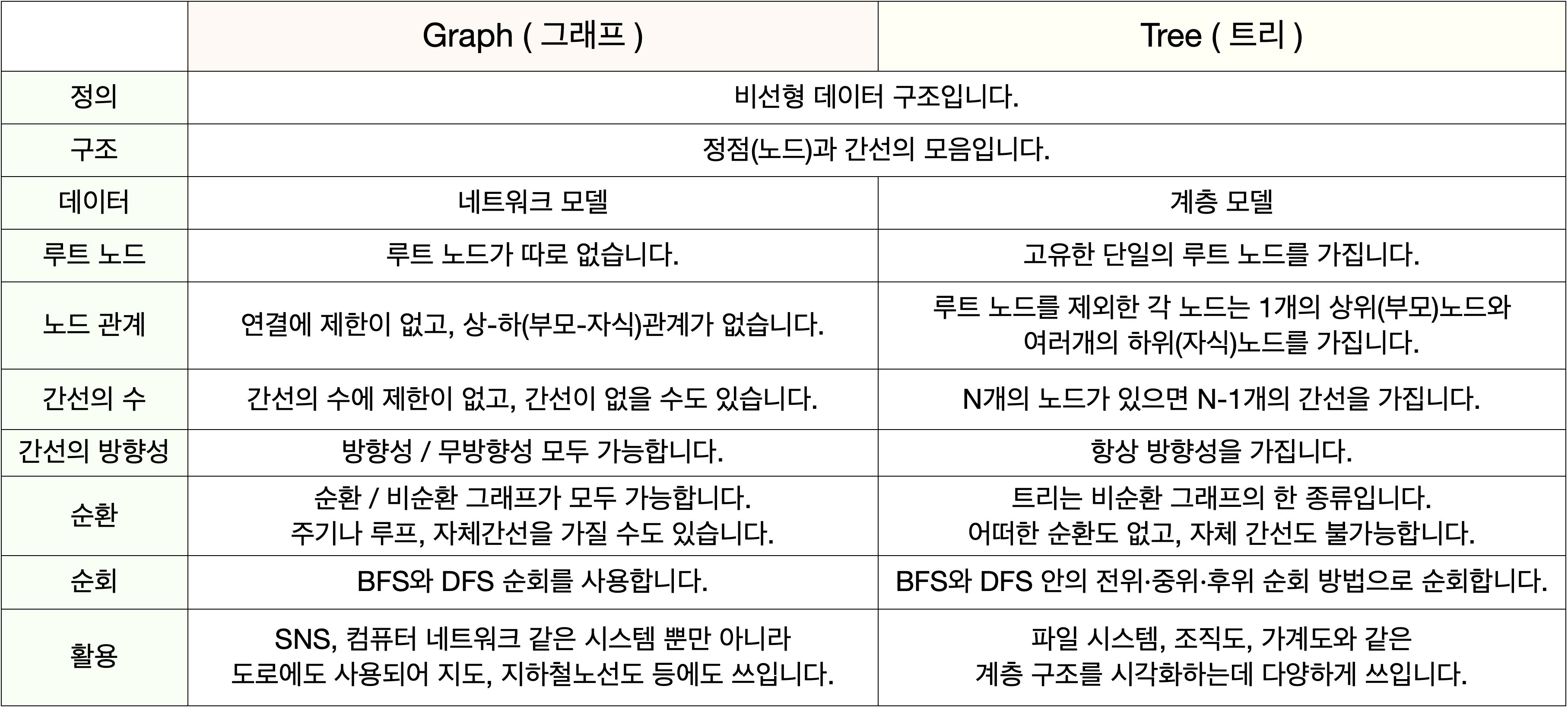
☀️ Characteristic of Graphs ( 특징 )

🪴 속 성

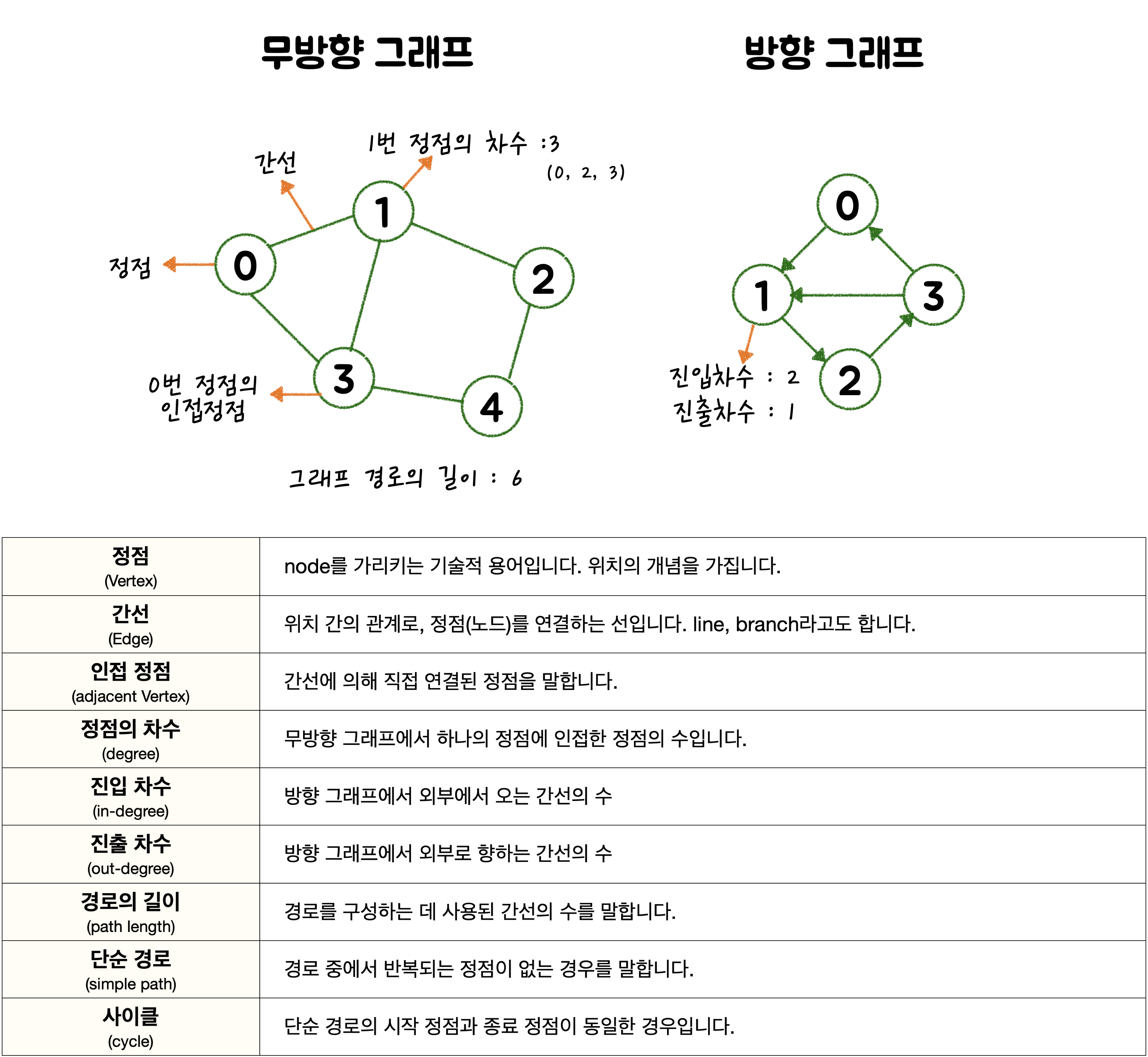
🙆🏻‍♀️ 장 점

  • 광범위한 관계와 다목적 데이터 구조를 나타내는 데 사용되어 문제를 해결합니다.

  • 복잡한 구조를 직관적이고 시각적인 방식으로 표현해서 이해하고 분석하기 좋아서 기계학습이나 모델링에 사용됩니다.

  • 대체 효율적이고 빠르게 데이터를 처리합니다.

🙅🏻‍♀️ 단 점

  • 그래프는 데이터를 제한하여 표현합니다. 데이터 간의 관계만 나타낼 뿐 개체의 속성이나 특징은 나타낼 수 없어서 완전한 이해를 위해서는 추가 정보로 보완해야만 합니다.

  • 데이터가 매우 크거나 복잡한 경우, 그래프를 생성하고 조작하기 위한 계산 비용이 비쌉니다. 애플리케이션이 확장하면서 노드나 간선의 수가 증가하면 분석하는 데 시간과 메모리가 많이 쓰이며 계산 비용이 더욱 많이 들어갑니다.

  • 이보다 더 데이터가 크거나 복잡하다면 시각화하고 분석하는 것 자체가 어려울 수 있습니다. 그렇다면 그래프로 의미있는 해석을 추출하기 어렵습니다.

  • 반대로 데이터가 매우 단순하거나 구조화된 경우, 그래프로 구현하는 것은 과도하게 느껴질 수 있고 불필요한 비용이 발생할 수 있습니다. 이 경우 다른 단순한 데이터 자료 구조로 충분히 표현할 수 있습니다.

  • 그래프는 데이터 품질에 영향을 많이 받습니다. 기반 데이터가 불완전하거나 일관성이 없거나 부정확하다면 데이터 간의 관계를 정확하게 반영하지 못합니다. 또한, 분석결과의 정확성에 영향을 미칠 수 있는 노이즈 및 이상값에 매우 취약합니다.

  • 그래프는 유형이 매우 다양합니다. 이것은 장점이기도 하지만 단점이기도 합니다. 각 유형마다 장·단점이 있고 선택에 대한 표준화된 자료가 부족하여 다양한 유형 중 어느것을 선택할 지에 어려움을 겪을 수 있습니다.

  • 그래프 이론이나 관련 알고리즘은 익숙하지 않다면 복잡하고 이해하기가 어렵습니다. 이에 따라 그래프 알고리즘을 올바르게 설계하고 구현하기 어려울 수 있으며, 버그나 오류가 생기기 쉽습니다. 또한 그래프의 해석은 주관적일 수 있으며 특별한 지식이 필요할 수도 있습니다.

🪴 활 용

그래프는 실생활 다양한 곳에서 쓰입니다. 다음은 그래프가 쓰이는 대표적인 예입니다.

  • 스포츠 팀에서 선수간 상호작용을 분석해 팀 역학과 개선 영역을 분석하고 개선합니다.

  • 검색 추천 엔진을 구성하는 데에도 그래프가 쓰입니다. 키워드가 겹치거나, 사람들이 이어서 클릭한 검색어, 검색어간 연관성, 공통점 등을 분석해서 추천합니다.

  • SNS에서 친구들과 연결 관계를 그래프로 판단합니다. 친구 네트워크를 표현하는 방식 중 하나입니다.

  • 지도에서 장소, 도로, 교통망의 장소간 연결(길)을 그래프로 표현하고, 이를 통해 최단거리, 속도제한, 교통상황 등을 취합해 최적의 경로를 추천합니다.

  • 공항을 정점으로, 항공경로를 간선으로, 거리를 가중치로 두어 항공로지도를 그래프로 표현할 수 있습니다.

  • 뇌 속 신경망은 네트워크와 유사합니다. 이를 그래프로 표현해 뇌를 이해해 의학적으로 사용합니다.

  • 서버를 노드로, data연결을 간선으로, 속도를 가중치로 해서 라우팅을 표현하는 데에도 쓰입니다.

    🌿 예시

☀️ Type of Graphs ( 유형 )

  • 그래프는 데이터에 따라 여러 가지 유형으로 표현할 수 있고, Tree 자료구조가 방향성 + 비순환 그래프인 것 처럼 여러 가지 유형을 포함할 수 있습니다.
  • 아래에서 설명하는 유형 외에도 무한그래프, 멀티그래프, 의사그래프 등 더 많은 유형이 존재합니다.

Null (널 그래프) vs Trivial (사소한 그래프)

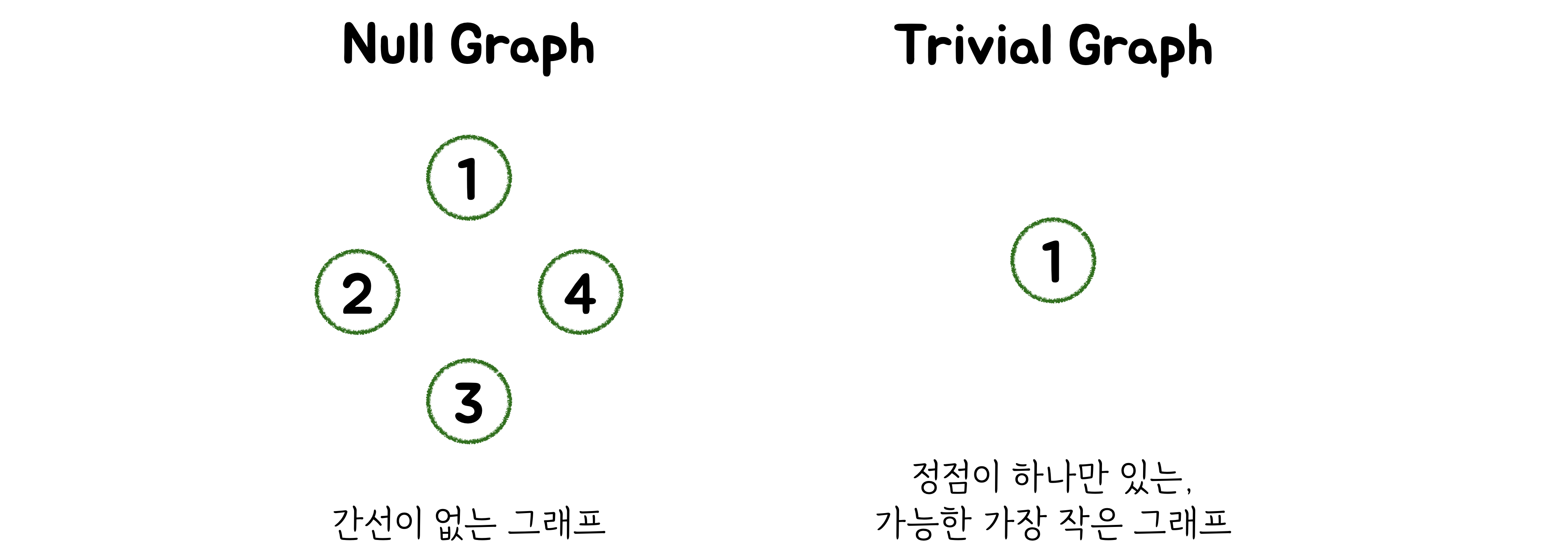
  • Null Graph는 경계가 없는 그래프, 고립된 그래프 또는 이산 그래프라고도 합니다.

  • Trivial Graph는 더 복잡한 그래프를 작성하기 위한 시작점으로 사용됩니다.

Undirected (무방향 그래프) vs Directed (방향 그래프)

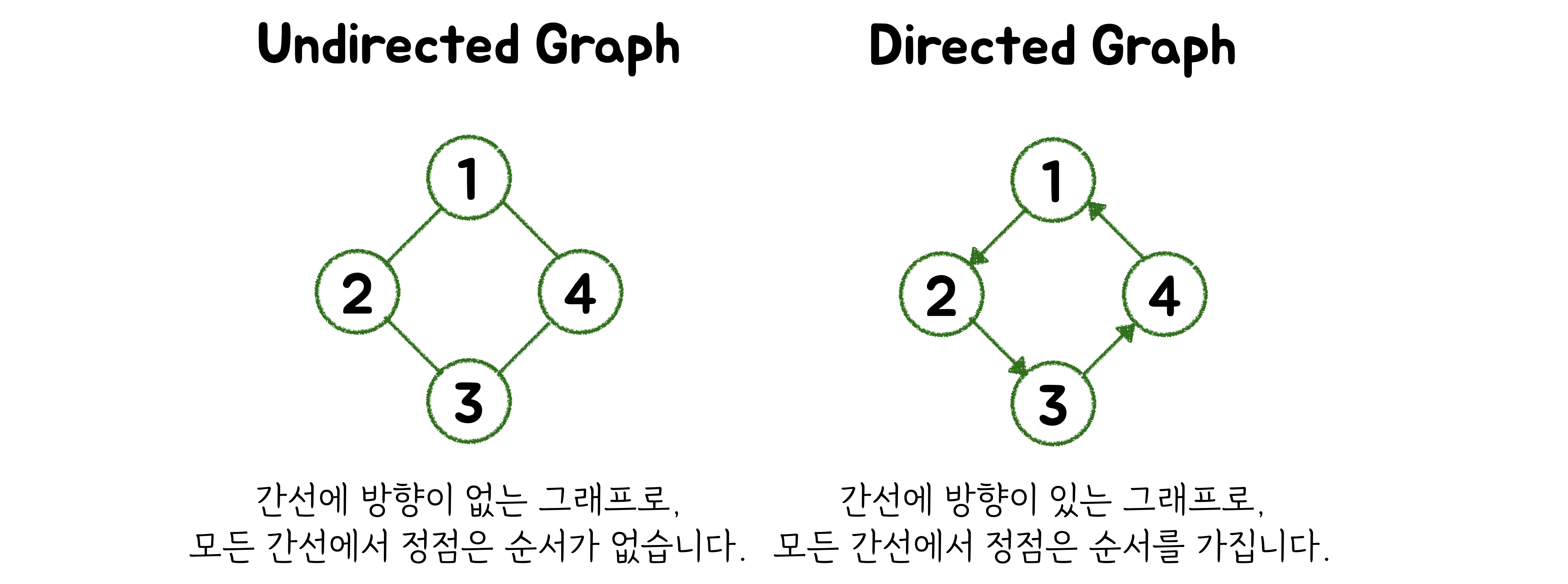
  • 무방향 그래프는 양방향 통행과 같고, 방향 그래프는 일방 통행과 같습니다. 간선은 보통 양방향 · 무방향 그래프가 보통입니다. 방향 그래프는 간선을 화살표로 하여 표현합니다.

  • 무방향 그래프는 간선을 (A, B), (B, A)와 같이 쌍으로 표현합니다. 방향 그래프는 <A, B> 로 표현하고 <A, B> 와 <B, A>는 다릅니다.

  • 무방향 그래프의 대표적인 예는 페이스북 친구 네트워크이고, 방향 그래프의 대표적인 예는 인스타나 트위터의 친구 네트워크입니다. 페이스북은 친구를 추가하면 쌍방이 친구로 추가됩니다. 하지만 인스타나 트위터같은 경우에는 한쪽이 친구 신청을 하고(방향이 있고) 상대방은 받아주거나 안받아줄 수 있습니다(한쪽만 친구로 추가할 수 있다).

Connected (연결 그래프) vs Disconnected (비연결 그래프)

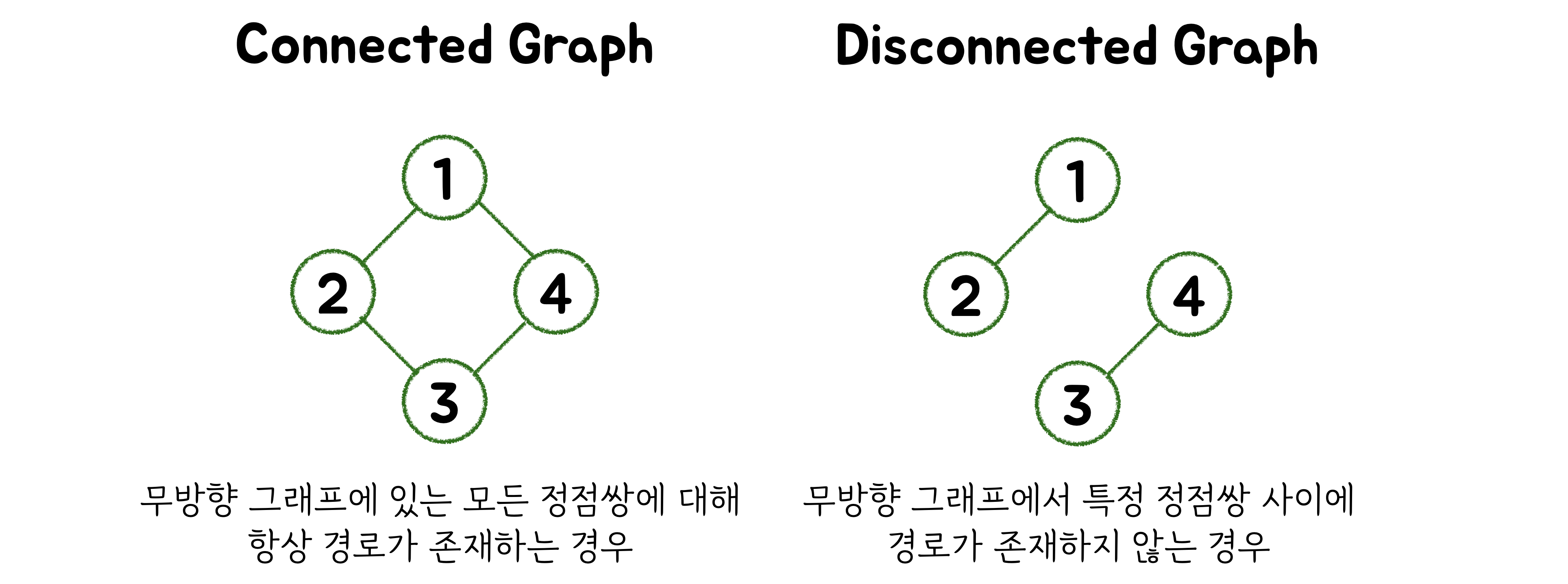
  • 트리는 대표적인 연결그래프 중 하나입니다.

Regular (정규 그래프) vs Complete (완전 그래프)

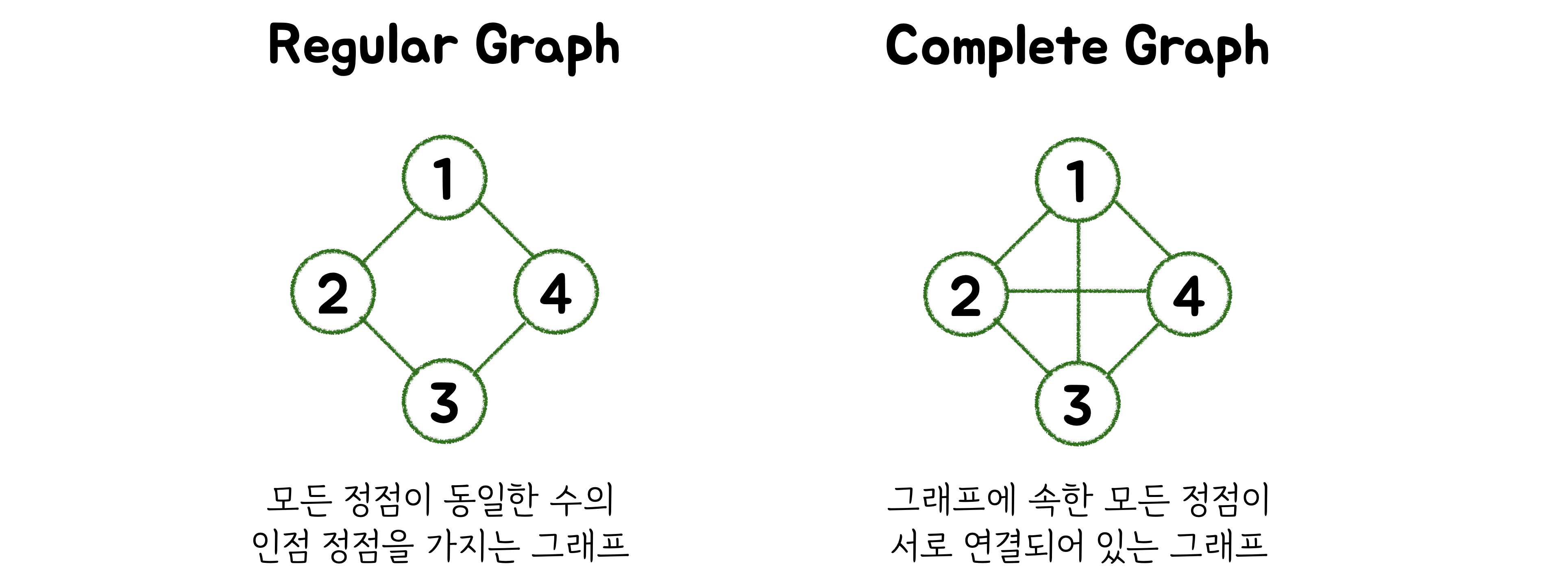
  • 완전그래프는 하나의 정점이 n - 1개의 간선을 가집니다. 즉, 하나의 정점은 자기자신을 제외한 나머지 모든 정점과 연결되어 있습니다.

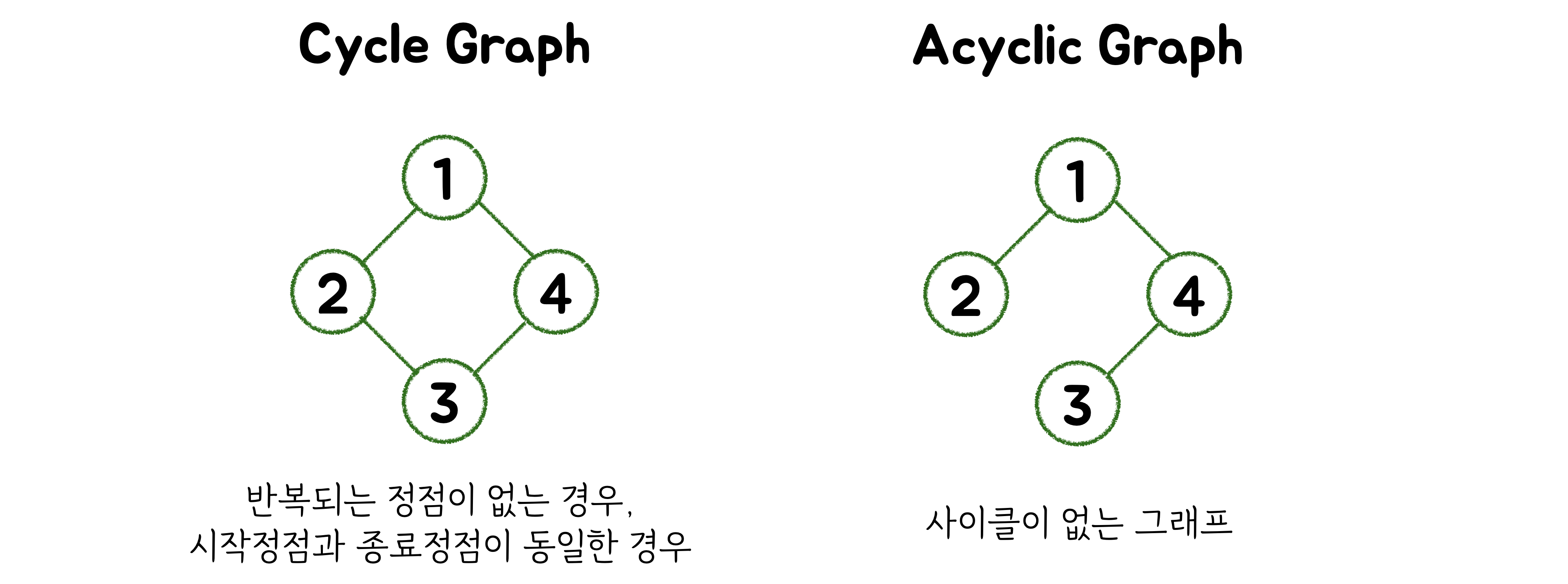
Cycle (순환 그래프) vs Acycle (비순환 그래프)

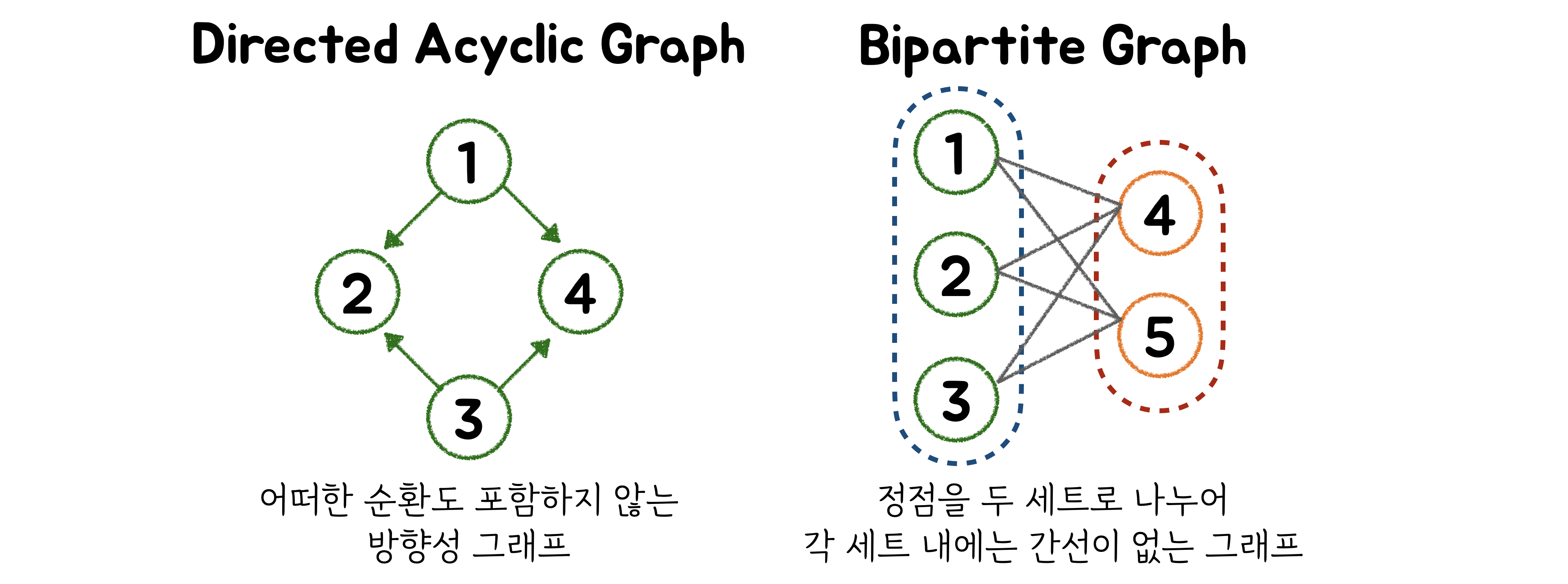
Directed Acyclic (방향성 비순환 그래프) vs Bipartite (이분 그래프)

Directed weighted (방향성 가중치 그래프) vs Undirected weighted (무방향성 가중치 그래프)

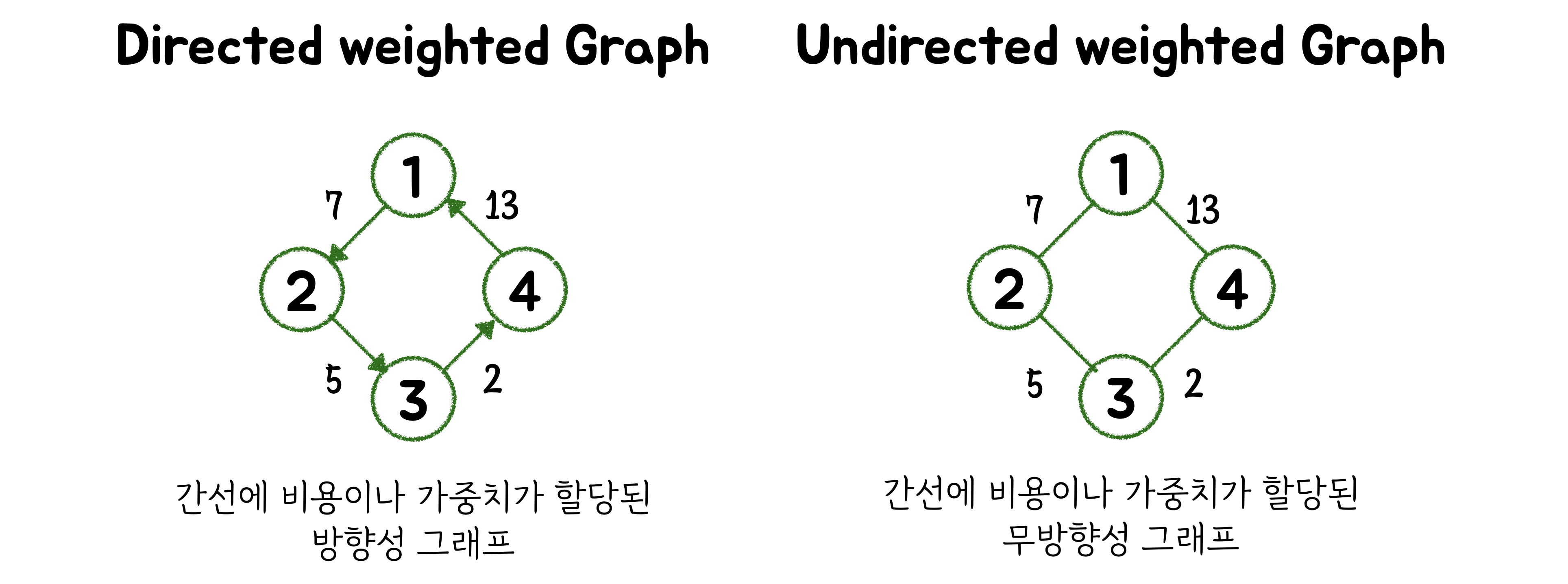
  • 가중치 그래프는 '네트워크(network)'라고도 하며, 간선에 할당된 비용이나 가중치의 대표적인 예는 지도에서의 거리입니다. 가중치는 연결 그 자체에 대한 정보를 표현합니다.
  • 가중치 그래프는 도로의 길이, 통신망의 사용료 등에 쓰여 최단거리 경로탐색 등이 대표적인 예입니다.

☀️ Implement of Graphs ( 구현 )

인접행렬과 인접리스트 두 가지 방법으로 그래프를 구현할 수 있습니다. (하지만 실제 최적의 자료구조는 두 구조의 조합된 형태로 사용된다고 합니다.)

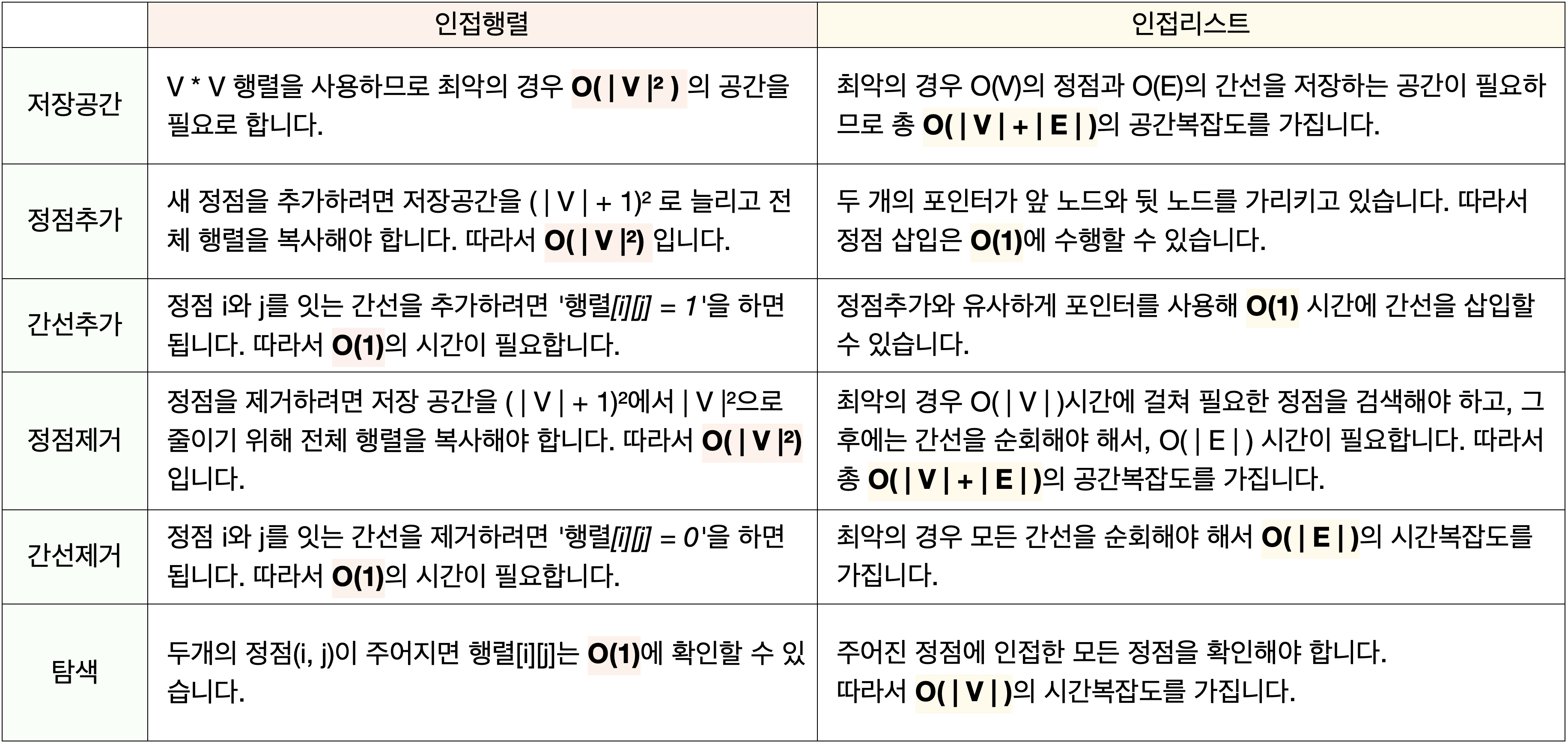
🪴 Adjacency Matrix of Graph ( 인접 행렬 )

// class로 인접 행렬 만들기
class Graph {
	constructor(n) {
		this.vertices = n;
		this.graph = [];
      	//initialize
		for (let i = 0; i < this.vertices; ++i) {
			this.graph[i] = [];
			for (let j = 0; j < this.vertices; ++j) {
				this.graph[i][j] = 0;
			}
		}
	}
}
// 함수로 인접행렬 만들기
let vertices = 0;

// 그래프 생성
const graph = Array.from(Array(10), ()=>Array(10).fill(0));
function initialize(n) {
	vertices = n;
	for(var i = 0; i < n; ++i) {
		for(var j = 0; j < n; ++j) {
			graph[i][j] = 0;
		}
	}
}
// 🖨️ print
function adjacencyMatrix() {
	for(var i = 0; i < n; ++i) {
		for(var j = 0; j < n; ++j) {
			console.log("," + graph[i][j]);
		}
	}
}

  • 인접행렬은 V * V 크기의 2D 배열입니다. V는 그래프 정점의 수이고, adj[i][j] = 1은 정점 i와 정점 j 사이에 간선이 있음을 나타냅니다. 행과 열이 정점을 나타내고 간선이 있으면 1(true), 없으면 0(false)로 나타내는 2차원 boolean Matrix 형태(보통 중첩 배열)로 그래프를 저장합니다.

  • 무방향 그래프의 인접행렬은 항상 대칭(대칭행렬, Symmetric Matrix)입니다.

  • 인접 행렬은 가중치 그래프를 나타내는 데에도 사용됩니다. abj[i][j] = w이면 정점i와 j사이 간선의 가중치가 'w'값임을 말합니다.

  • 그래프에 간선이 많이 존재하고, 행렬의 일부만 비어있는 밀집 그래프의 경우를 나타내기 적합합니다. 밀집 그래프의 경우, 두 정점을 연결하는 간선의 존재여부를 O(1)만에 알 수 있습니다. 정점의 차수는 O(n)만에 알 수 있습니다. 하지만 인접 정점을 알기 위해서는 모든 노드를 순회해야 하므로 O(n²)이 걸립니다. 이 때 간선이 없는 빈공간까지 저장하고 순환하므로 퍼져있는 데이터에 적합하지 않고, 이런 면에서 인접 리스트보다 효율성이 떨어집니다.

  • 간선의 수와 무관하게 정점의 개수가 n개인 그래프는 n²의 메모리 공간을 필요로 합니다.

🕶️ 인접 행렬 그래프에서 간선 추가 및 제거

간선의 삽입 및 삭제는 O(1)이 걸리지만, 표시하는 데 O(n²)이 필요합니다.

// 간선 추가
function addEdge(x, y) {
	if ((x >== vertices) || (y > vertices)) console.log(`정점이 존재하지 않습니다 🤷🏻‍♀️`);
  	if (x === y) console.log("같은 정점을 입력했어요!🤦🏻‍♀️");
	else {
		graph[y][x] = 1;
		graph[x][y] = 1;
	}
}

// 간선 제거
function removeEdge(x, y) {
	if ((x >== vertices) || (y > vertices)) console.log(`정점이 존재하지 않습니다 🤷🏻‍♀️`);
	if (x === y) console.log("같은 정점을 입력했어요!🤦🏻‍♀️");
	else {
		graph[y][x] = 0;
		graph[x][y] = 0;
	}
}
// 그래프 method 로 구현
	addEdge(x, y){
		if ((x >== vertices) || (y > vertices)) console.log(`정점이 존재하지 않습니다 🤷🏻‍♀️`);
  		if (x === y) console.log("같은 정점을 입력했어요!🤦🏻‍♀️");
		else {
			this.graph[y][x] = 1;
			this.graph[x][y] = 1;
		}
	}
	
	removeEdge(x, y) {
    	if (x >= this.vertices || y >= this.vertices) console.log(`정점이 존재하지 않습니다 🤷🏻‍♀️`);
    	if (x === y) console.log("같은 정점을 입력했어요!🤦🏻‍♀️");
    	else {
      		this.graph[y][x] = 0;
      		this.graph[x][y] = 0;
    	}
  	}

🕶️ 인접 행렬 그래프에서 정점 추가 및 제거

// 정점 추가
function addVertex() {
	vertices++;
	let i;
  
	for (i = 0; i < vertices; ++i) {
		graph[i][vertices - 1] = 0;
		graph[vertices - 1][i] = 0;
	}
}

// 정점 제거
function removeVertex(x) {
	if (x > vertices) {
		console.log("정점이 존재하지 않아요!🙅🏻‍♀️");
		return;
	} else {
		let i;
		while (x < vertices) {
 			for (i = 0; i < vertices; ++i) {
				graph[i][x] = graph[i][x + 1];
			}
			for (i = 0; i < vertices; ++i) {
				graph[x][i] = graph[x + 1][i];
			}
			x++;
		}
		vertices--;
	}
}
// 클래스 문법
	addVertex() {
		this.vertices++;
		let i;
		for (i = 0; i < this.vertices; ++i) {
			this.graph[i][this.vertices - 1] = 0;
			this.graph[this.vertices - 1][i] = 0;
		}
	}
	
	removeVertex(x) {
		if (x > this.vertices) {
			document.write("Vertex not present!<br>");
			return;
		} else {
			let i;
			while (x < this.vertices) {
				for (i = 0; i < this.vertices; ++i) {
					this.graph[i][x] = this.graph[i][x + 1];
				}
				for (i = 0; i < this.vertices; ++i) {
					this.graph[x][i] = this.graph[x + 1][i];
				}
				x++;
			}
			this.vertice--;
		}
	}
	
}

🪴 Adjacency List of Graph ( 인접 리스트 )

class AdjacencyList {
  constructor() {
    // 간선을 저장할 proeperty만 있으면 족합니다.
    this.adj = {};
  }

  • 가장 일반적인 그래프를 표현하는 방법으로, 연결된 리스트의 첫번째 노드에 정점을 저장하고 연결된 나머지 리스트에 각 정점에 연결된 인접 정점들의 리스트를 배열이나 연결리스트로 표현합니다. 정점의 수만큼 배열의 크기를 가집니다. 노드의 key가 숫자가 아니라면 hass table 이나 dictionary, object, map등의 자료구조를 사용합니다.

  • 배열이나 인접 리스트로 표현한 경우, 정점의 번호를 인덱스로 가지므로 각 정점의 리스트에 쉽게 접근할 수 있습니다.

  • 간선이 많지 않고 퍼진 희소그래프의 경우, 데이터의 공간을 덜 차지하고 인접한 정점들을 쉽게 찾을 수 있습니다. 모든 간선의 수는 O(N + E)만에 알 수 있습니다.

  • 인접리스트는 간선에 가중치를 저장하도록 변형하여 가중치 그래프를 나타내는 데에도 사용할 수 있습니다.

🕶️ 인접 리스트 그래프에서 간선 추가 및 제거

  addEdge(vertex1, vertex2) {
    // vertex1의 key를 찾아 vertex2를 배열에 넣어줍니다. vertex2에서도 똑같이 진행합니다. (무방향graph 기준)
    if (!this.adj[vertex1]) this.adj[vertex1] = [];
    if (!this.adj[vertex2]) this.adj[vertex2] = [];
    this.adj[vertex1].push(vertex2);
    this.adj[vertex2].push(vertex1);
  }

  // 간선 제거에는 평균적으로 O(|E| / |V|)시간복잡도가 걸립니다.
  deleteEdge(vertex1, vertex2) {
    // filter method는 undefined에 작동하지 않아, 빈 배열이 있다면 에러날 수 있으므로 예외 처리 要
    if (!this.adj[vertex1] || !this.adj[vertex2]) return;
    
    this.adj[vertex1] = this.adj[vertex1].filter(v => v !== vertex2);
    this.adj[vertex2] = this.adj[vertex2].filter(v => v !== vertex1);
  }

🕶️ 인접 리스트 그래프에서 정점 추가 및 제거

	addVertex(key) {
	    if (!this.adj[key]) this.adj[key] = [];
    }

	deleteVertex(vertex) {
    	// 정점에 연결된 모든 간선도 제거해야 하므로 다른 정점도 모두 확인해야 합니다.
    	// 해당 vertex의 간선을 모두 순회합니다.
    	while(this.adj[vertex].length) {
          const adjvertex = this.adj[vertex].pop();
          this.deleteEdge(vertex, adjvertex);
        }
      	// 간선을 전부 제거한 후 key를 마저 제거합니다ㅣ.
      	delete this.adj[vertex];
      	// 보통은 delete 대신에 키를 비우거나 undefined로 설정합니다.
    }
}

👀 Reference

profile
NewHa
백 번을 보면 한 가지는 안다 👀

0개의 댓글