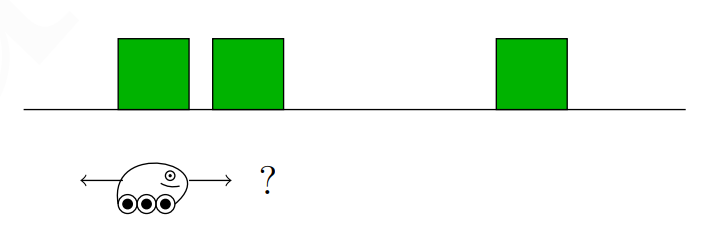로봇공학에서 굉장히 중요한 부분인 localization을 배웠다. 개념적으로 보았을때 localization은 로봇공학에서 알파벳 같은 느낌이 들었다. 결국 로봇을 사용하려면 로봇이 세상에서, 혹은 work-space에서 자기 자신/자신의 일부가 확률적으로 어디에 존재하는지 아는 것이 굉장히 중요하기 때문이다.
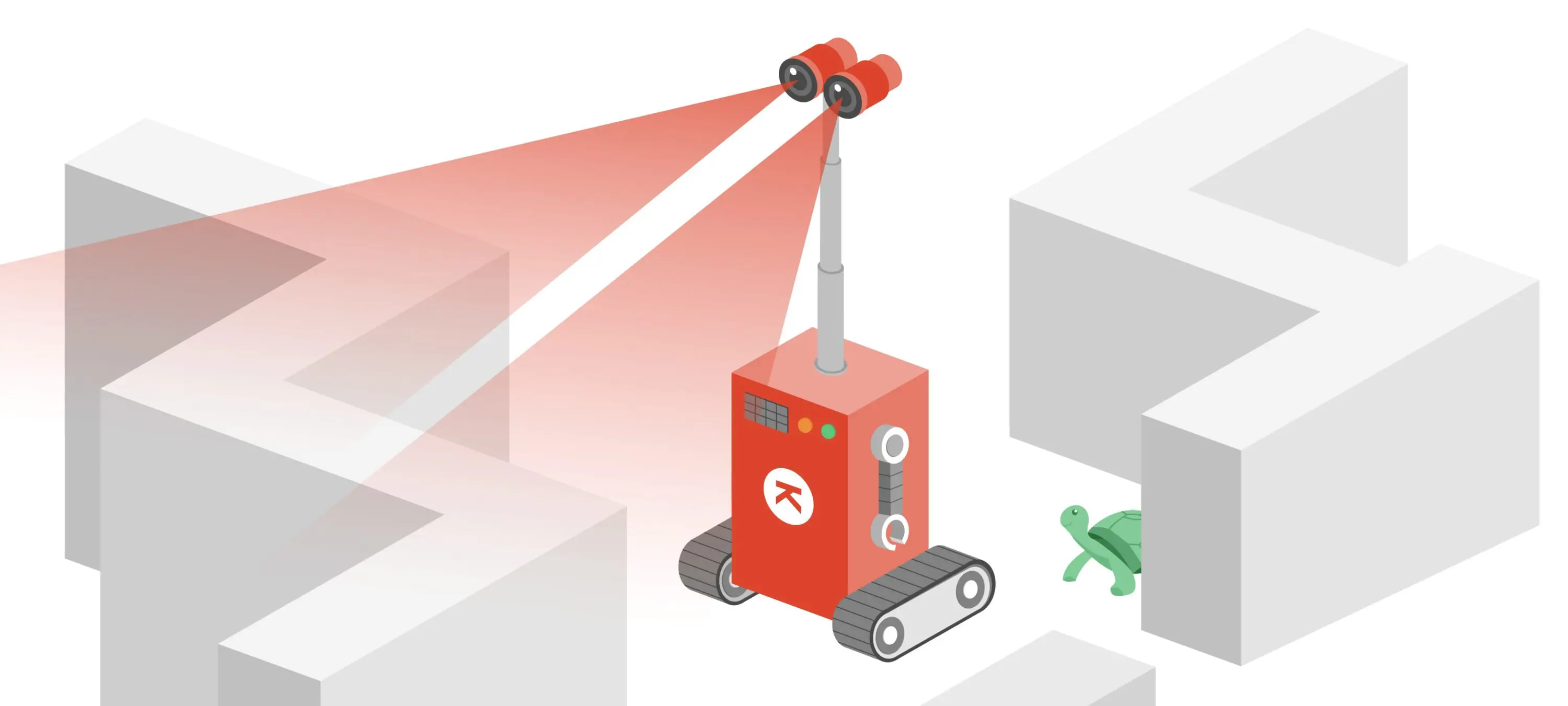
로봇이 세상에 어디에 있는지를 알기 위해서는 (이번 예제에서는 '로봇 본인이 세상에 어디에 있는지를 알기 위해'로 가정한다. 우리는 로봇이 이미 어디에 위치해 있는지 알고 있다고 가정하고 글을 쓴다), 조금 수학적인 접근이 필요하다. 만약에 그림과 같이 로봇이 3개의 문을 가지고 있는 복도 어딘가에 존재한다면 로봇은 본인의 위치를 어떻게 알 수 있을까?
그림 1
로봇이 복도 안 어딘가에 있다는 것을 알 수 있지만, 로봇 본인이 복도 정확히 어디에 있는지는 알기가 어렵다. 문제를 간단화 하기 위해 복도를 7개의 섹션으로 나눈다고 가정해본다. 복도가 7개의 섹션으로 나누어져 있다는 정보를 제외하면 우리에게 주어진 로봇의 정보는 아무것도 없기 때문에 각 섹션 별 로봇이 존재할 "확률" (확률이라고 표현한 것이 중요하다. 우리는 앞으로 로봇의 위치, 각도, 이동의 정도를 모두 "확률"적으로 표현 할 것이다) 은 1/7이 될 것 이다. 그래서 위의 이미지를 기반으로 각 위치/섹션에 로봇이 존재할 확률을 그래프로 표현한다면 밑의 그림과 같이 나올 것 이다.
그림 2
지금처럼 보이는 이 모든구역에서의 상태가 시작 단계이며, 강의에서는 prior 이라고 부른다. 영어에서 prior to ~something 이런식으로 많이 표현을 하는데 뭐뭐 하기전에~ 라는 뜻을 가지고 있다. 즉 이 컨텍스트에서 prior이란 어떠한 측정 이전 값/확률 을 나타내는 상태인 것 이다. 아무것도 측정하지 않았으니 모든 구역에서 1/7 확률인것... 이랄까나?
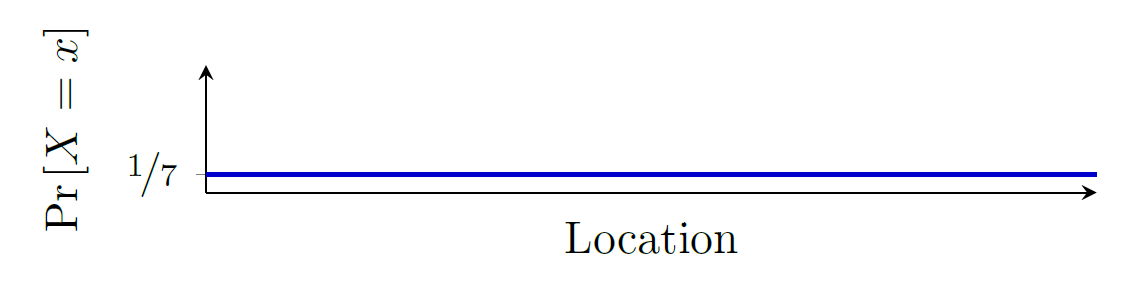
이제 로봇이 주변 환경을 측정하기 시작한다. 맨 위의 그림처럼 로봇이 제일 왼쪽 문에 있었다고 가정을 해 보면 (절대적 위치 값은 2. 밑의 그림을 보면 무슨 뜻인지 더 이해가 쉬울 것 같다), 로봇이 본인 앞에 문이 있다는 것을 확인 할 수가 있다. 이 측정값은 로봇에게 굉장히 큰 힌트를 주는 것이다. 내 앞에 문이 있으니 지금 내 위치는 정확히 어딘지는 모르겠지만, 7개의 섹션 중 문이 있는 섹션에 위치해 있을 확률이 높겠군! 이라고 판단을 내릴 것이다. 그것을 기반으로 본인이 위치한 곳의 확률 분포를 밑의 그림과 같이 재정립한다. 그리고 이 재정립 한 상태를 우리는 posterior 이라 부른다. Prior와 다르게 posterior는 ~~후 라는 뜻으로 받아들이면 된다. 쉽게말하면 prior 는 측정 전의 분포값, 그리고 posterior는 측정 후의 분포값이라 생각하면 되겠다. 이제 하나의 prior-posterior 세트가 생긴 것이다...!
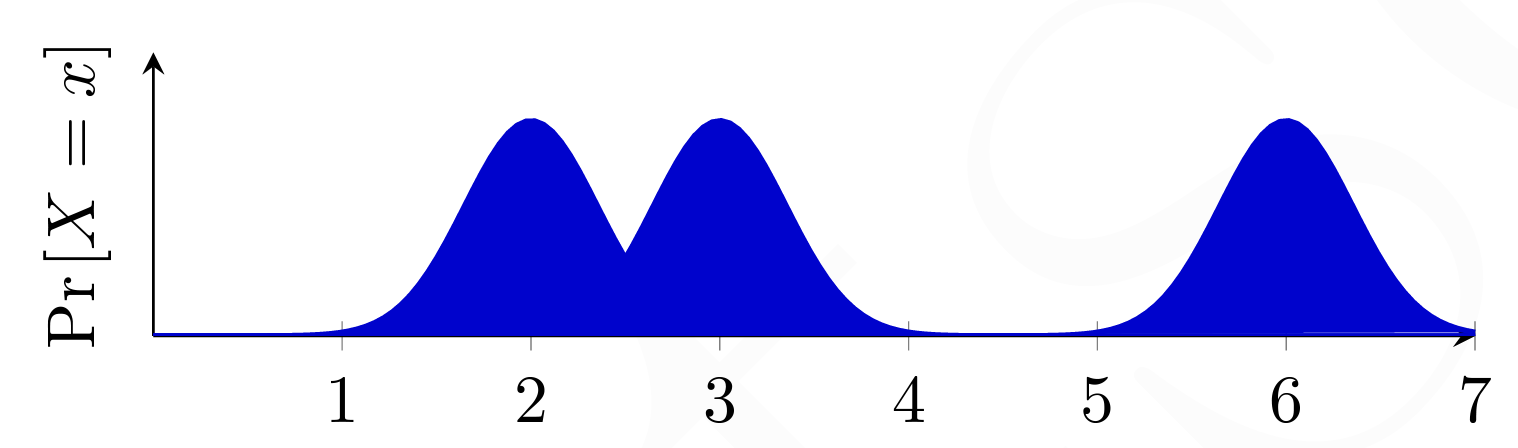
그림 3
2,3,6번에 문이 있는 것을 알고 있기 때문에, 로봇 앞에 문이 있다면 높은 확률로 그 로봇의 위치는 2,3,6중의 하나임을 의미한다. 하지만 0,1,4,5,7에도 미미 하지만 아주 작은 파란색이 칠해져 있다. 그 이유는 우리가 나머지위치에 로봇이 절대 100% 없다고 확언할 수 없기 때문이다. 센서가 고장이 났을 수도 있고, 문이 아닌 다를 물체를 로봇이 문이라고 잘못 인식했을 가능성 등 여러 이유로 오류측정을 할 가능성이 조금이라도 있을 수 있기 때문이다.
참고) 파란색 영역의 합을 구하면 1이 나온다. 로봇이 그 방 어딘가에는 존재하기 때문에, 그 방 안에 있는 각 섹션에 존재할 확률을 모두 합한다면 100%가 나오는 것
밑의 그림과 같이 이제 로봇이 오른쪽으로 (2에서 3으로) 한칸 움직일 예정이다.
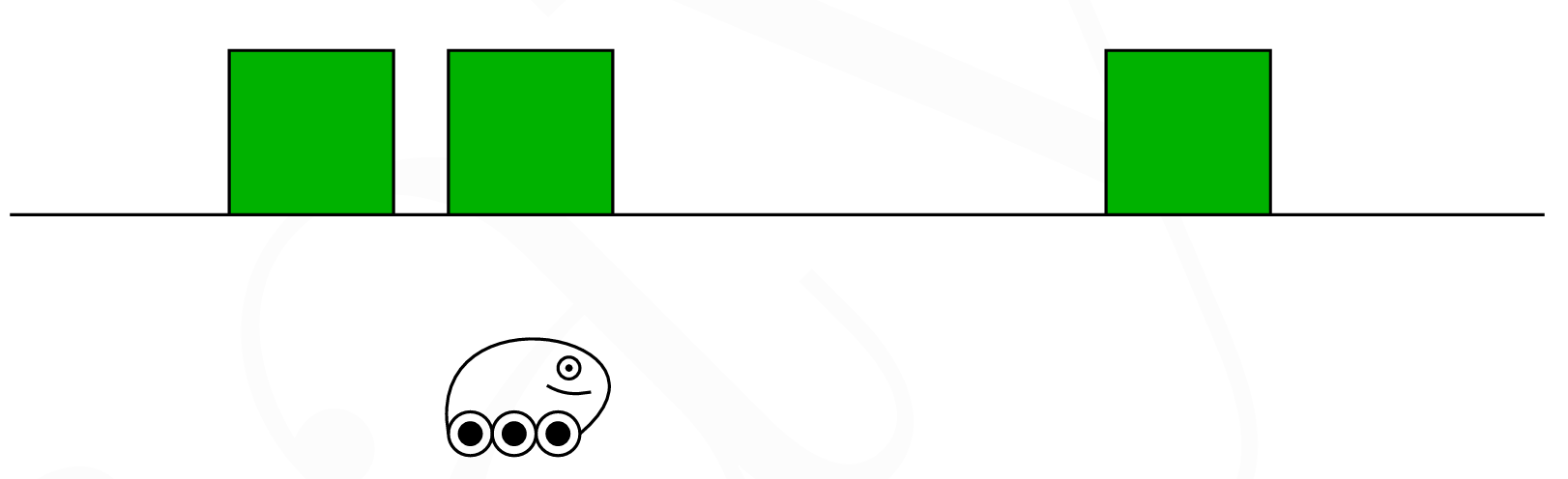
그림 4
처음 로봇이 본인이 어디에 있는지 (자기 앞에 문이 있다는 것을 확인했을때) 측정했을 때를 t0 라고 한다면, 이제 로봇이 움직였으니 t0+1 or t1 이 되었다. t0일때 posterior였던 그림 3을 기반으로 로봇은 나름대로 추측을 하게 된다. "내가 아까 2,3,6에 있었을 확률이 높았었지. 내가 그 3개중에 어디에 위치했었을지 정확히는 모르지만 만약 한칸 오른쪽으로 이동했다면 이제 내가 이 복도에서는 위치 할 확률이 그림 5와 같이 나오겠구나" 라는 결론을 낼 것이다.
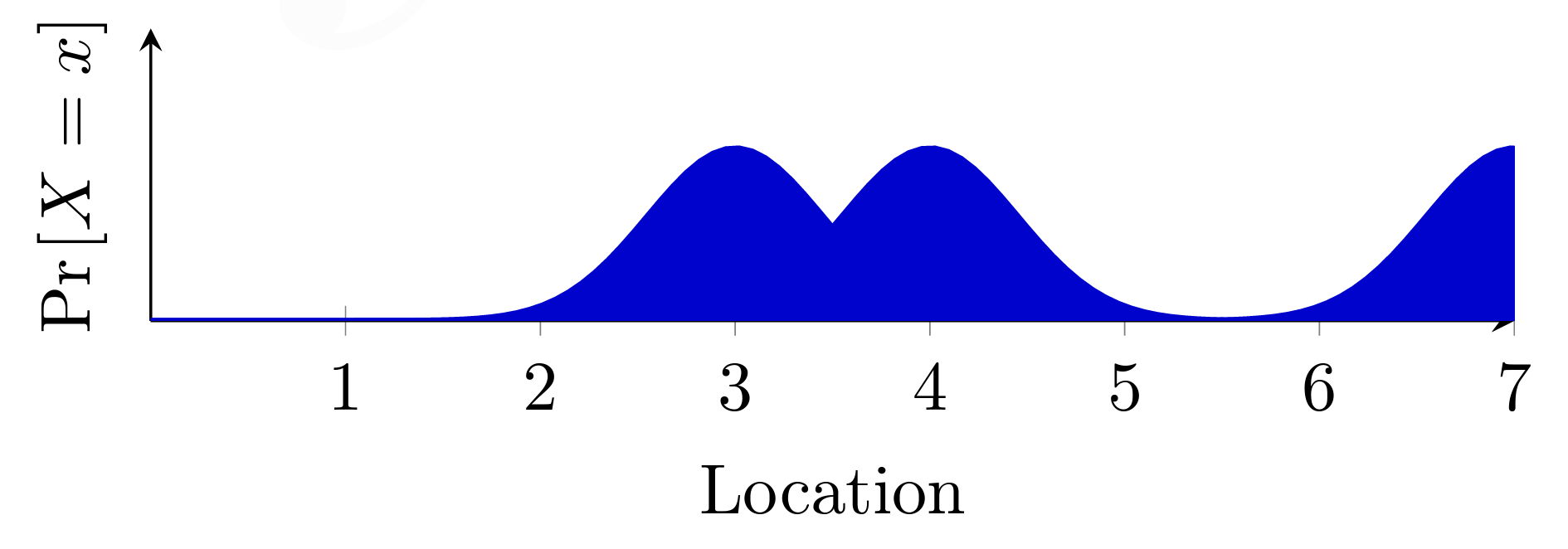
그림 5
2에 있던 봉우리가 3으로, 3에있던 봉우리가 4로 ... , 로봇이 본인의 위치가 있을 확률 분포를 한칸 씩 오른쪽으로 이동한 것을 알 수 있다. 그림이 조금 작아서 눈치 못 챈 사람도 있겠지만 그림 3과 비교했을 때 그림 5의 봉우리가 조금 낮아진 것을 알 수 있다. 왜 이런일이 일어났을까? 위에 잠깐 설명했던 이유와 비슷하게, 로봇이 1.00000000000000000 만큼 우측으로 정확하게 이동했을 확률이 100%가 아니기 때문이다. 로봇 모터가 이상이 있었을 수도, 바닥이 울퉁불퉁했을 수도, 아무튼 여러가지 이유로 정확히 1만큼 오른쪽으로 갔다고 로봇이 100% 장담하지 않기 때문이다. 고로 로봇은 오류가 생겼다고 가정을 하고 본인 위치의 확률을 조금 낮게 책정한 것이다. 지금 이 상태가 prior 이다. 이제 로봇이 자기의 센서를 이용하여 posterior 분포를 나타낼 수 있을 것이다.
로봇은 t0일때 문을 보았고, t1에 우측으로 한칸 이동하였는데 또 문이 보였다. 그림 1의 복도대로라면 로봇이 t0에 어디서 시작했고 t1에 어디인지 바로 확인 할 수가 있다. 로봇은 2의 위치에서 시작했고 지금 우측으로 한칸 이동한 3에 존재할 것이다. 문-문을 설명하기엔 그 경우의 수밖에 없기 때문이다. 그렇기에 로봇은 밑과 같은 posterior 분포를 줄 것이다.
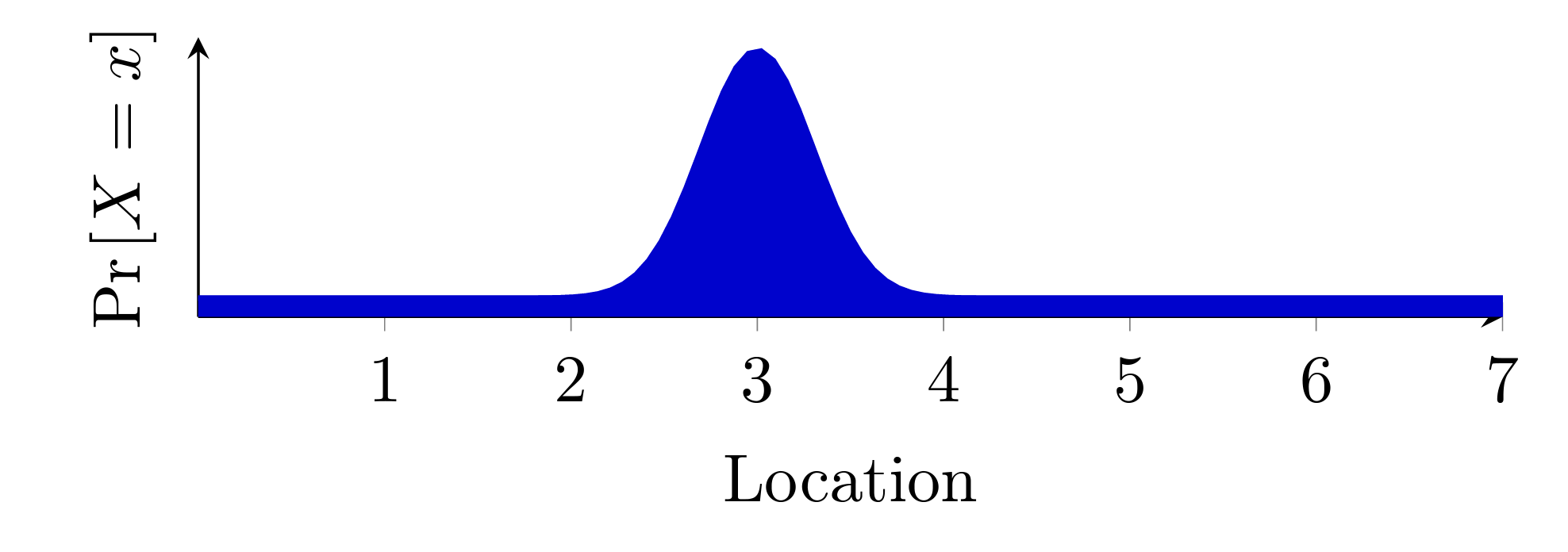
그림 6
이것이 확률에 기반한 로봇의 localization 개념이다!