Localization with Python

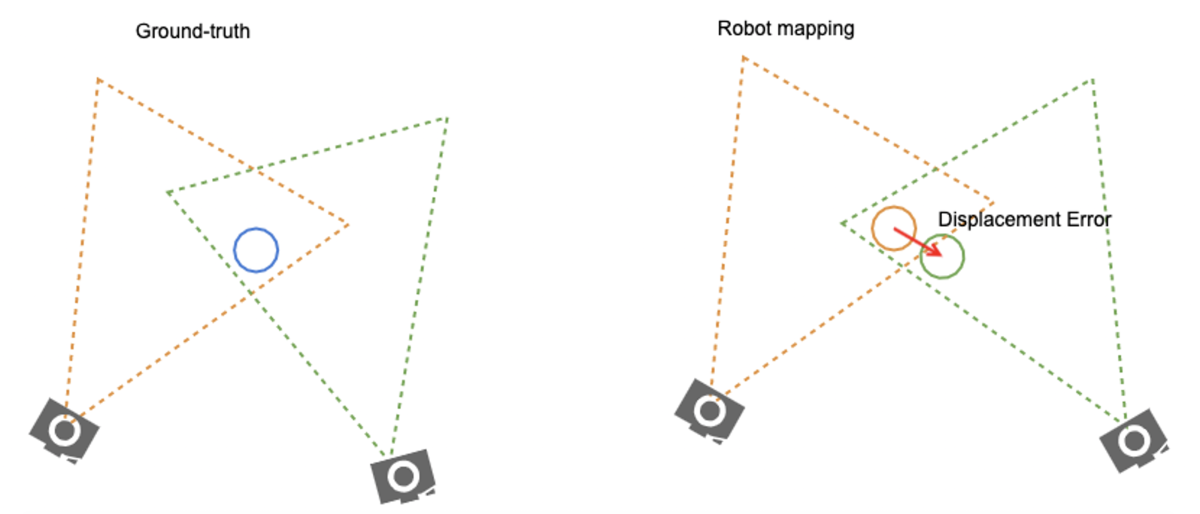
저번 주에 올렸던 포스팅과 이어서 확률에 기반한 로봇의 위치 인식에 대해 예제와 함께 알아보겠다. 저번 주 포스팅에서는 7개의 색션과 3개의 문을 가진 복도로 예제를 설명했지만 이번에는 조금 다른 (개념적으로는 동일함) 예제로 포스팅을 써보려고 한다. 예제의 환경을 맵이라고 부르도록 하겠다 (게임에서도 유즈맵처럼 그냥 환경을 맵으로 부르는 것 같아서 여기서도 사용하겠다). 이번 맵은 5개의 색션으로 나누어 져 있으며 3개의 초록 블락, 그리고 2개의 빨간 블락으로 구성되어 있다.

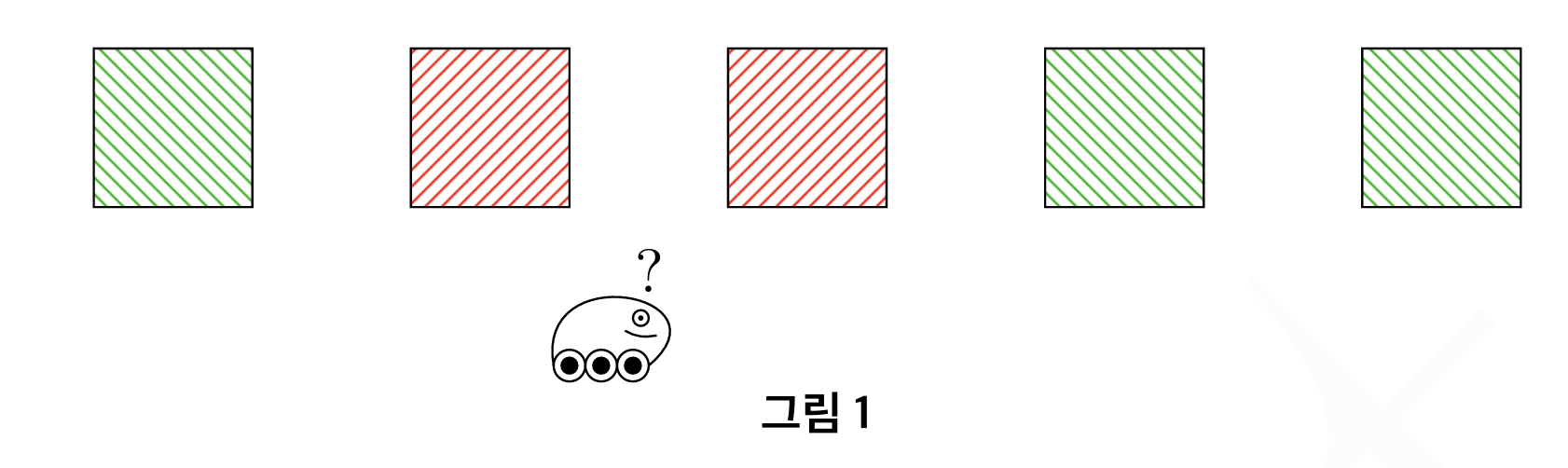
늘 그러하듯 우리 로봇은 멍청하기 때문에 본인의 위치를 정확하게 알지 못한다. 아직 측정을 하지 않은 prior 상태에서 로봇의 존재 확률은 각 섹션마다 0.2 혹은 1/5의 값을 가지고 있다. 여기서부터 조금 예제가 달라진다. 저번 예제와는 다르게 이번 예제에서는 로봇이 정확하게 빨간색을 빨간색으로 & 초록색을 초록색으로 인식할 확률이 (pHit) 60% or 0.6으로 설정을 하고 빨간색을 초록 & 초록을 빨간색으로 인식할 확률을 (pMiss) 20% or 0.2라고 설정을 해보자.

강의에서 이 숫자를 채택하여 사용했는데 사실 좀 이상하긴 하다. 그냥 6 대 4 혹은 5 대 5 이런식으로 합해서 100% or 1이 나오는 깔끔한 숫자를 사용했으면 조금 더 직관적이었을 것 같기는 한데... 조교들도 정확히 "왜" 이 0.6, 0.2를 사용했는지는 알 수 없다. 이렇게 넘어가면 설명이 부족할 것 같아서 강의 조교들의 답변을 그래도 복붙하여 공유한다 (영어인 점 참고바란다...).

이제 주어진 0.6과 0.2 값을 이용해 Prior값을 기반으로 posterior 를 유도하는데, 방법이 매우 간단하다. 그림 1처럼 로봇이 2번칸 (왼쪽에서 2번째칸 (빨강색)) 에 있었고 측정을 했을때 본인이 0.6의 확률로 빨강 앞에 있다는 결과가 나왔다고 가정해보자. 그렇다면 prior 확률 분포도의 초록-빨강-빨강-초록-초록 섹션에서 빨강 값을 가진 섹션에 0.6을 곱해주고 그렇지 않은 칸에는 0.2를 곱해준다. 밑의 그림을 참고해보자.

그렇게 되면 0.04 0.12.... 이런 posterior 값이 나오게 된다. 이 값들이 로봇이 있을 확률을 나타내주는 확률 분포도에 해당하게 되지만 사실 직관적인 숫자들은 아니다. 0.12가 빨강에 있을 확률을 12% 라고 말해주는 것일까? 그렇지 않다. 왜냐하면 normalized (정규화)가 되지 않았기 때문이다. 우리는 이 값들을 사람들이 조금 더 직관적으로 알 수 있는 백분위의 숫자로 normalize를 시켜주어야 한다. 하는 방법은 간단한데, 각각의 값들을 다 더하고 그 값을 각각의 확률에 나누어주면 된다. 그림 3을 참고하자.

이렇게 되면 우리가 생각하는 정규화된 확률을 찾아 낼 수가 있다. 33.33...% 로 로봇은 2번칸 혹은 3번칸에 존재하게 된다. 그리고 나머지 33.333...%의 확률로 1,4,5번칸에 존재하게 되는데, 이게 저번 주차에 얘기한 봉우리를 제외한 구역에도 얇은 파란 영역 에 해당하게 되는 것이다. 물론 저번 주차에서 사용한 그래프처럼 봉우리를 제외한 나머지 부분이 거의 없으려면 0.6, 0.2의 숫자보다 각 숫자의 차이가 훨씬 커야 할 것이다 (0.9, 0.1 뭐 이런식으로..).

만약에 로봇에 여기서 한칸 더 오른쪽으로 가고 또 다시 빨간색을 봤다면 어떻게 해야할까? 그냥 위에 나온 1/9,1/3...1/9 의 값이 prior가 되며, 동일한 방법으로 0.6&0.2 값을 곱해주고 노멀라이즈 시켜주면 될 것 같지만 세상은 그렇게 호락호락하지 않다. 로봇의 움직임 또한 반영해야하며 그 것은 다음 주차의 포스팅에서 다루도록 하겠다. 다만 연구적 접근(?) 차원에서 그냥 위의 방법을 채택하면 나오는 결과물 또한 보여주도록 하겠다.

파이썬 코드

p=[0.2,0.2,0.2,0.2,0.2] # 초기 prior 값 설정
t=['green','red','red','green','green'] # 색 위치 설정
pHit = 0.6 # 주어진 pHit & pMiss 값 설정
pMiss = 0.2

def sense(p,Z):
    q=[]
    for i in range(len(p)):
        # 만약 로봇이 본 색깔과 해당 인덱스의 색 값이 같다면 1(True) 다르다면 0(False)
        hit = (Z == world[i])
        # 위의 hit 값을 기반으로 각 인덱스 값에 0.6 or 0.2 곱함
        q.append(p[i] * (pHit*hit + pMiss*(1-hit))) 
    # 정규화 (Normalize 는 여기서 해줌)
    s = sum(q)
    for j in range(len(q)):
        # 소수점이 너무 길어져서 5번째자리 까지만 출력
        q[j] = round(q[j] / s, 5)
    return q

observed = ['red']
for j in range(len(observed)):
    p = sense(p,observed[j])
print(p)

결과:

[0.11111, 0.33333, 0.33333, 0.11111, 0.11111]

위에 말했던 것 처럼 두번 세번 움직여보자. 똑같은 코드를 돌리면 되는데 밑에서 4번째 줄인

observed = ['red']

만

observed = ['red','red'] 아니면 observed = ['red','red','green']

이런식으로 바꾸어 주면 된다. 그렇게 된다면 각각의 결과 값은 이렇게 나온다.

['red','red']: [0.04762, 0.42857, 0.42857, 0.04762, 0.04762]
['red','red','green']: [0.11111, 0.33333, 0.33333, 0.11111, 0.11111]

값들이 뭔가 심상치 않다.

로봇은 항상 sense -> move, sense -> move를 반복하는데 우리의 코드는 sense,sense,sense 만 하고 있는 셈이다. 그렇게 때문에 이상한 값들이 나오게 된 것인데, 다음 주차에는 이 move를 어떻게 적용시키는지 알아보도록 하겠다.

0.6과 0.2 확률에 관한 학생의 질문과 TA분의 답변:

질문: From the lectures, pHit is 0.6 and pMiss is 0.2. Why do these values not add up to 1? How does sensor_right from PS1 relate to the parameters pHit and pMiss from the lectures?

pHit is the probability that the sensor is correct (which defines the probabilities for both of the following):

• pHit = P(Red|Red)

• pHit = P(Green|Green)

pMiss is the probability that the sensor is wrong (which defines the probabilities for both of the following):

• pMiss = P(Red|Green)

• pMiss = P(Green|Red)

It doesn't necessarily have to be the case that the True red rate and the True green rate are the same, but in this problem they were defined to be the same. For whatever reason, the sensor could be better at correctly detecting red than correctly detecting green.

Therefore, pHit corresponds to sensor_right and pMiss corresponds to sensor_wrong.

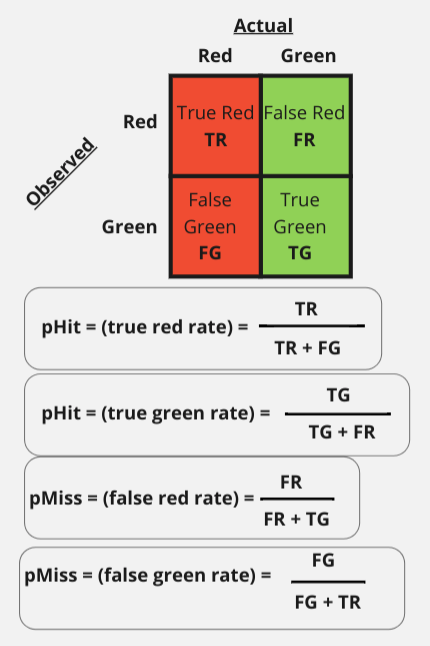
The following must be true of normalized probabilities:

• P(Red|Red) + P(Green|Red) =1

• P(Green|Green) + P(Red|Green) =1

Since the values provided by Dr. Thrun for pHit and pMiss don't sum to 1, they must represent non-normalized probabilities (which can be normalized).

I don't know why he chose to provide non-normalized values here, it is a very odd choice, especially in a pedagogical context where it only adds confusion. Any non-normalized values that hold the same relationship could have also been provided, and the outcome would still be the same, ie: (150 & 50, 300 & 100, .9 & .3, etc..).