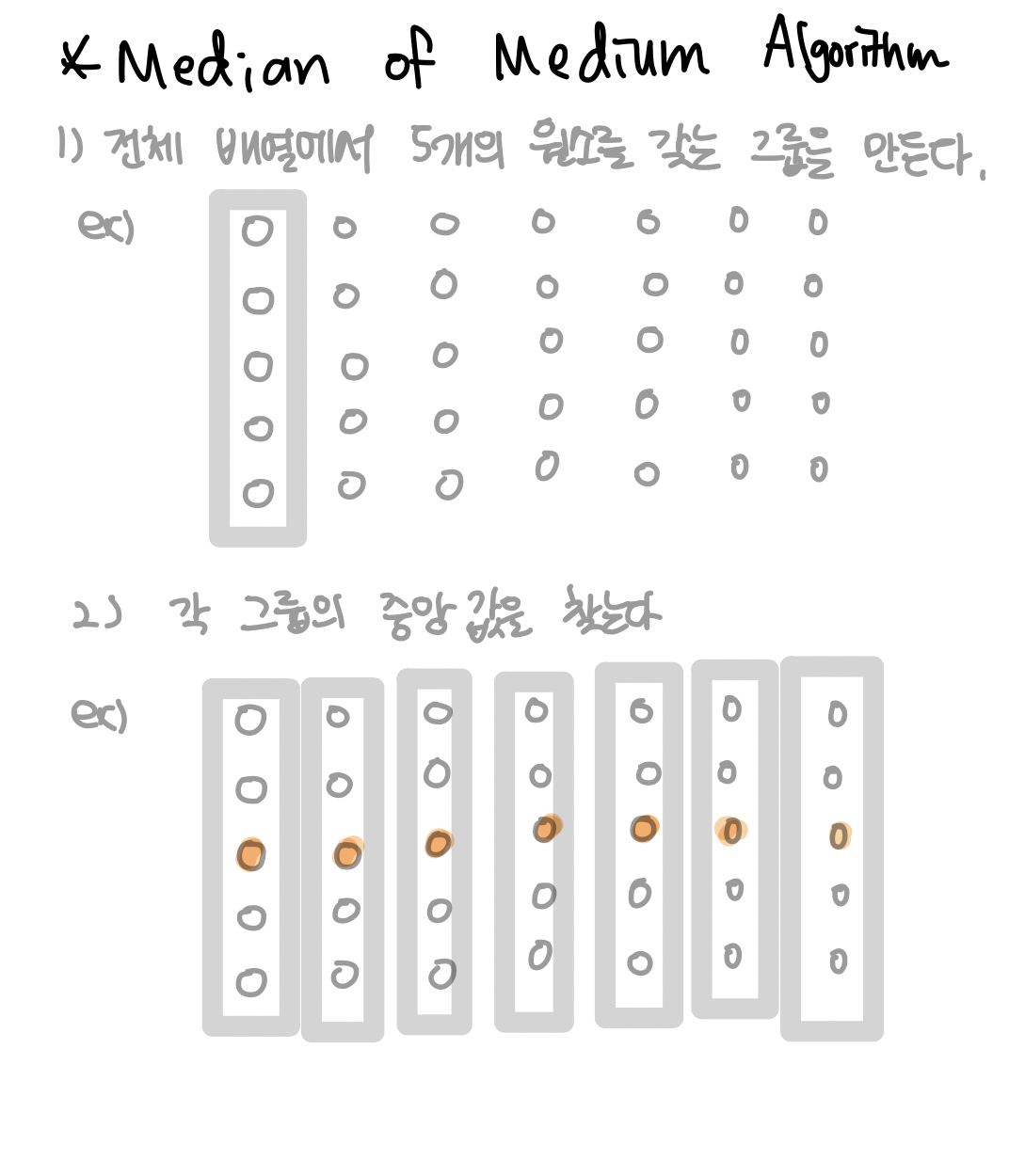
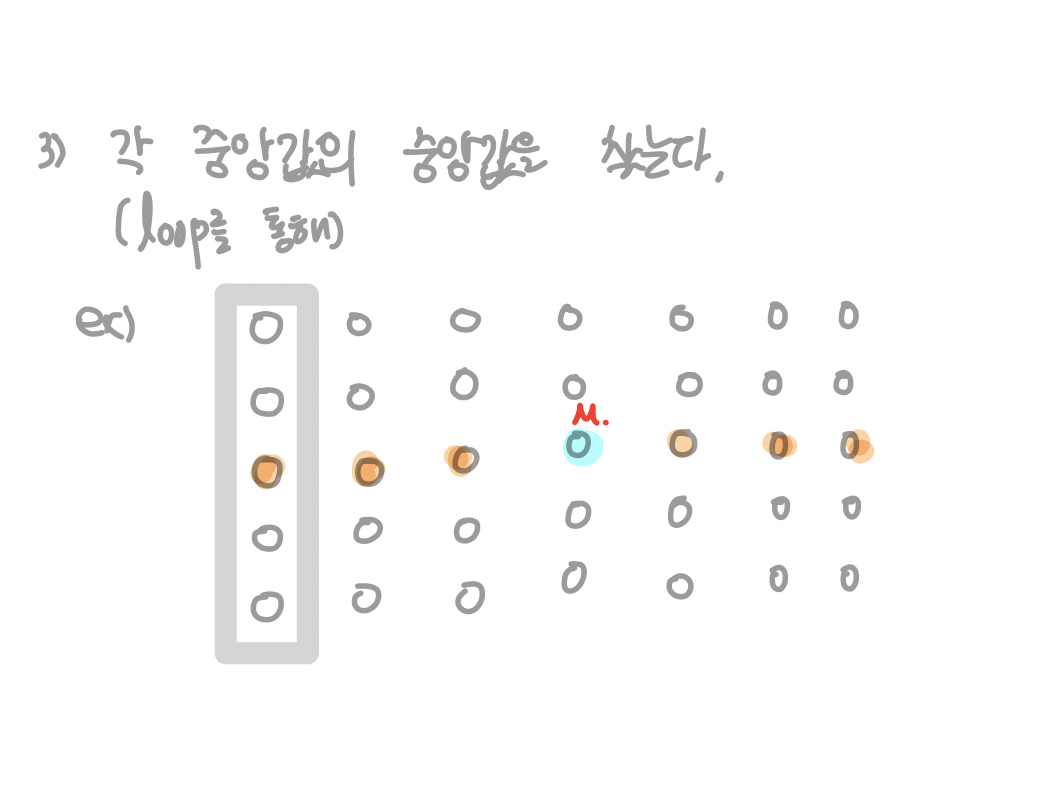
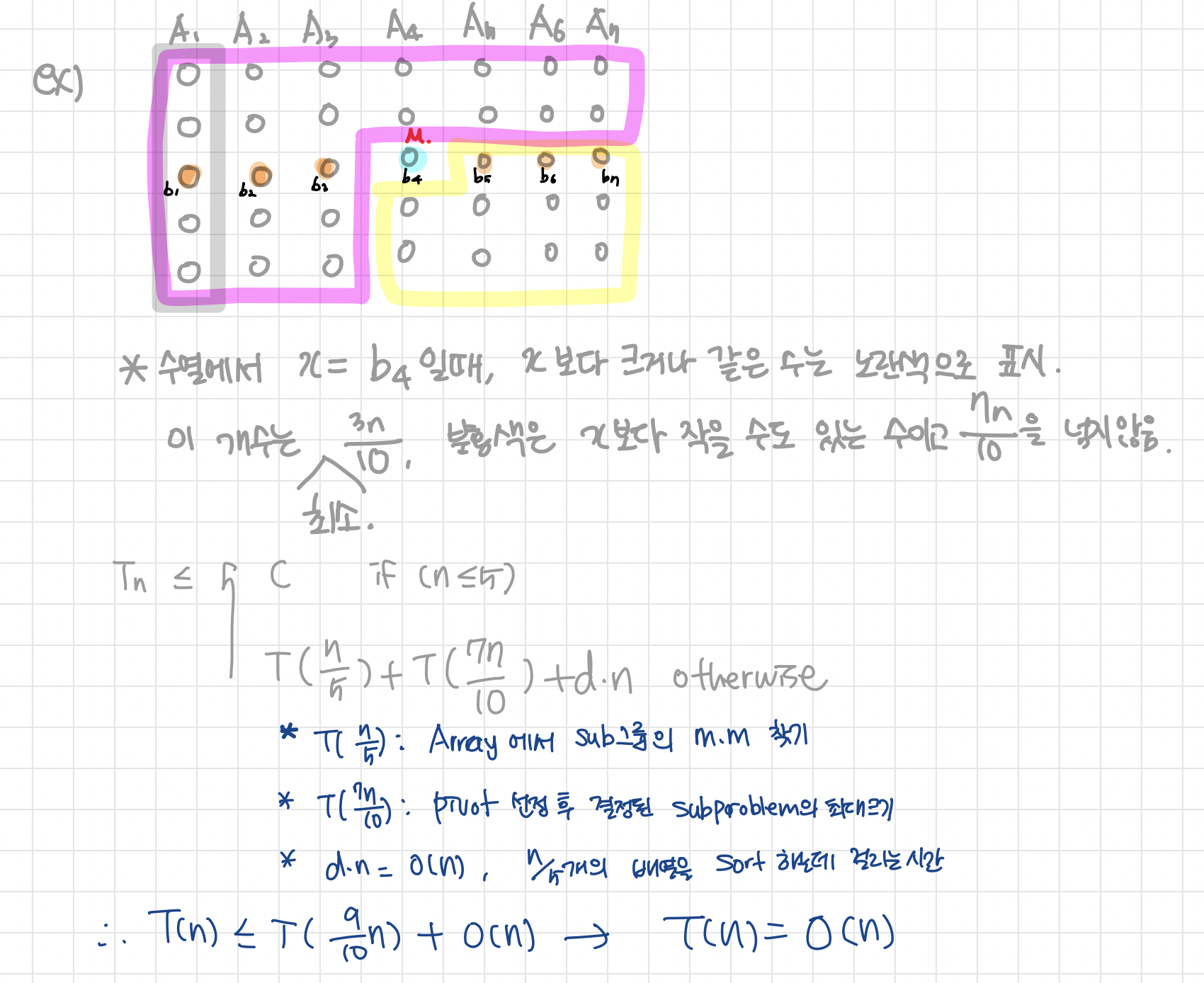
1. Describe linear median finding algorithm. Show that its time complexity is Θ(n).
퀵 정렬(Quick Sort)를 이용하는 방법
1) Divide & Conquer
2) Randomize
주어진 수열에서 임의로 숫자 x를 pivot으로 설정.
이 pivot은 기준점으로 작용하여 pivot을 기준으로 pivot보다 작은 숫자와 큰 숫자로 분류.
작은 숫자들의 개수를 i라고 할 때, 만약 k≤i이라면 k번째로 작은 숫자는 x보다 작은 숫자일 것이므로 x보다 작은 숫자들 중에서 k번째로 작은 숫자를 찾는다.
반대로 k>i라면, x보다 크거나 같은 숫자들 중에 존재할 것이기 때문에 그 숫자들 중에서 k−i번째로 작은 숫자를 찾는다.
이를 수열의 길이가 1이 될 때까지 loop를 돈다.
c.f) pivot보다 작은 값을 왼쪽으로 이동, pivot보다 큰 값을 오른쪽으로 이동함. index를 활용하며 루프를 돌면서 swap.
3) Variants
3-1) Basic QS
n의 길이를 갖는 수열에서 퀵 선택이 쓰는 시간을 T(n)이라고 하였을 때,
시간복잡도는 다음과 같다.
만약 pivot x가 최소값 A[0]이거나 최댓값 A[n-1] 이라면, 시간복잡도는 O()으로 굉장히 오랜시간이 소요되는 최악의 경우가 발생.
3-2) Intelligent QS
2. In hashing function, why the coefficient a should not be 0?
1) 해시함수
h(k) = ((ak + b) mod p) mod m
a가 0인경우 ak값이 0이되어 해시함수에 key값이 아무런 영향을 주지 못하여 a값의 범위는 0<a<p-1이어야한다.
b: noise, 0<b<p-1
p: 충분히 큰 소수
0 ≤ k ≤ p-1
p > m
m: 줄이고 싶은 space 크기
3. If the keys are uniformly distributed and n = 2m, every unsuccessful search requires only 2m/m = 2 comparisons, and the average number of comparisons for a successful search is
Theorem 8.4 : If n keys are uniformly distributed in m buckets, the number of comparisons in an unsuccessful search is given by n/m.
✔️n개의 key가 균일하게 m개의 버킷에 분류되어있는 경우 실패한 검색의 비교 횟수는 n/m번이다.
Theorem 8.5
If n keys are uniformly distributed in m buckets and each key is equally likely to be the search key, the average number of comparisons in a successful search is given by (n/2m)+1/2
✔️각 버킷의 평균 검색 시간은 n/m 키를 순차적으로 검색할 때의 평균 검색 시간과 동일하다.
n=2m일때, n/m=2. n/2m+1/2=3/2임을 알 수 있다.