1. Read chapters 7.1 – 7.7.
2. Solve the exercise problem 14 of the chapter 7.
Show that the time complexity for the number of assignments of records for the Mergesort algorithm (Algorithms 2.2 and 2.4) is approximated by T (n) = 2n lg n.
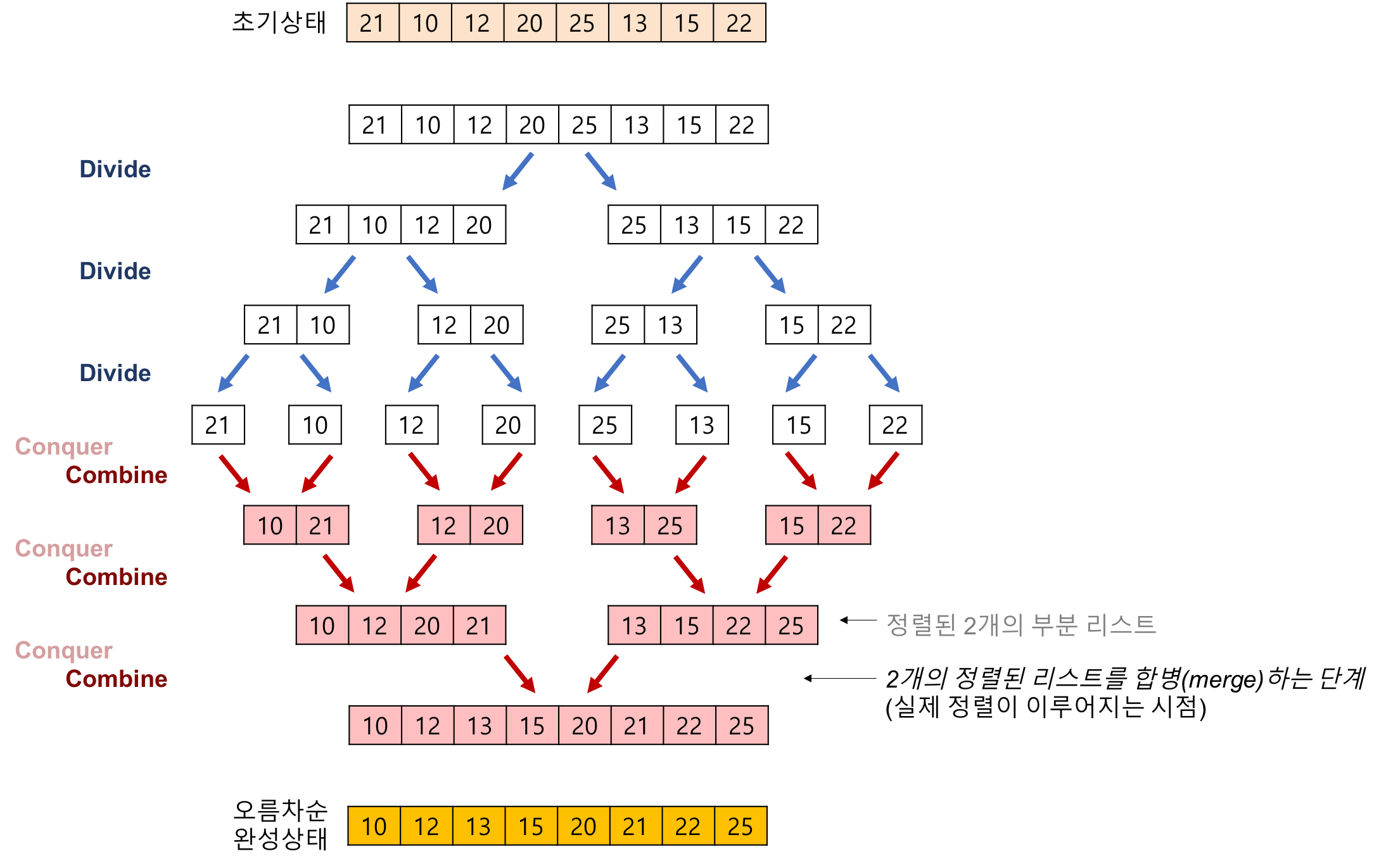
합병정렬 알고리즘
- 리스트의 길이가 0 또는 1이면 이미 정렬된 것으로 본다. 그렇지 않은 경우에는 정렬되지 않은 리스트를 절반으로 잘라 비슷한 크기의 두 부분 리스트로 나눈다.
- 각 부분 리스트를 재귀적으로 합병 정렬을 이용해 정렬한다.
- 두 부분 리스트를 다시 하나의 정렬된 리스트로 합병한다.
합병정렬 알고리즘은 다음과 같다.
def merge_sort(a):
def sort(unsorted_list):
if len(unsorted_list) <= 1:
return
# 두개의 리스트로 분할. 아래에서 재귀적으로 시행
mid = len(unsorted_list) // 2
left = unsorted_list[:mid]
right = unsorted_list[mid:]
merge_sort(left)
merge_sort(right)
merge(left, right)
def merge(left, right):
i = 0
j = 0
k = 0
while (i < len(left)) and (j < len(right)):
if left[i] < right[j]:
a[k] = left[i]
i += 1
k += 1
else:
a[k] = right[j]
j += 1
k += 1
# 남은 데이터 삽입
while i < len(left):
a[k] = left[i]
i += 1
k += 1
while j < len(right):
a[k] = right[j]
j += 1
k += 1
print(a)
sort(a)
array = [21,10,12,20,25,13,15,22]
merge_sort(array)합병정렬의 시간복잡도 구하기
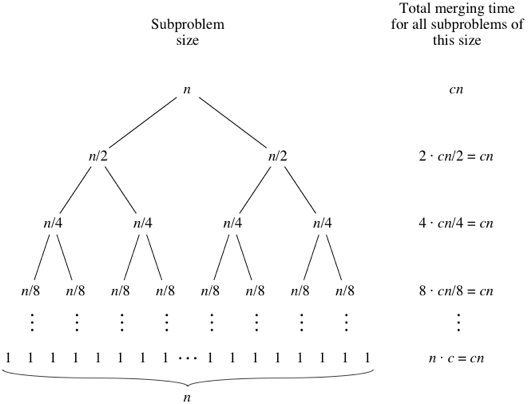
- 크기 1인 부분 배열 2개를 병합하는 데 걸리는 연산 횟수는 최대 2번 이다.
총 4 쌍이므로 2 4 = 8 이라는 연산 횟수가 도출된다. 다음으로 크기 2인 부분 배열 2개를 병합하게 된다. 이 때 걸리는 연산 횟수는 최대 4번이다. 총 2쌍이므로 4 2 = 8 이라는 연산 횟수가 도출 된다. 마지막으로 크기 4인 부분 배열 2개를 병합하면 최대 8번의 연산횟수가 도출된다. 즉 각 단계별로 걸리는 연산횟수는 최대 n 번이다. - 순환 깊이는 2씩 나눠지므로 logN 이다. 총 연산횟수는 NlogN 이다.
- 다음으로 이동할 때 드는 연산이 존재한다. 임시 배열에 하나씩 이동시키므로 크기 1인 경우 2번, 크기 2인 경우 4번... 총 이동은 2n 번 발생한다. 이 또한 깊이만큼 곱하면 2NlogN 이라는 연산횟수가 도출된다.
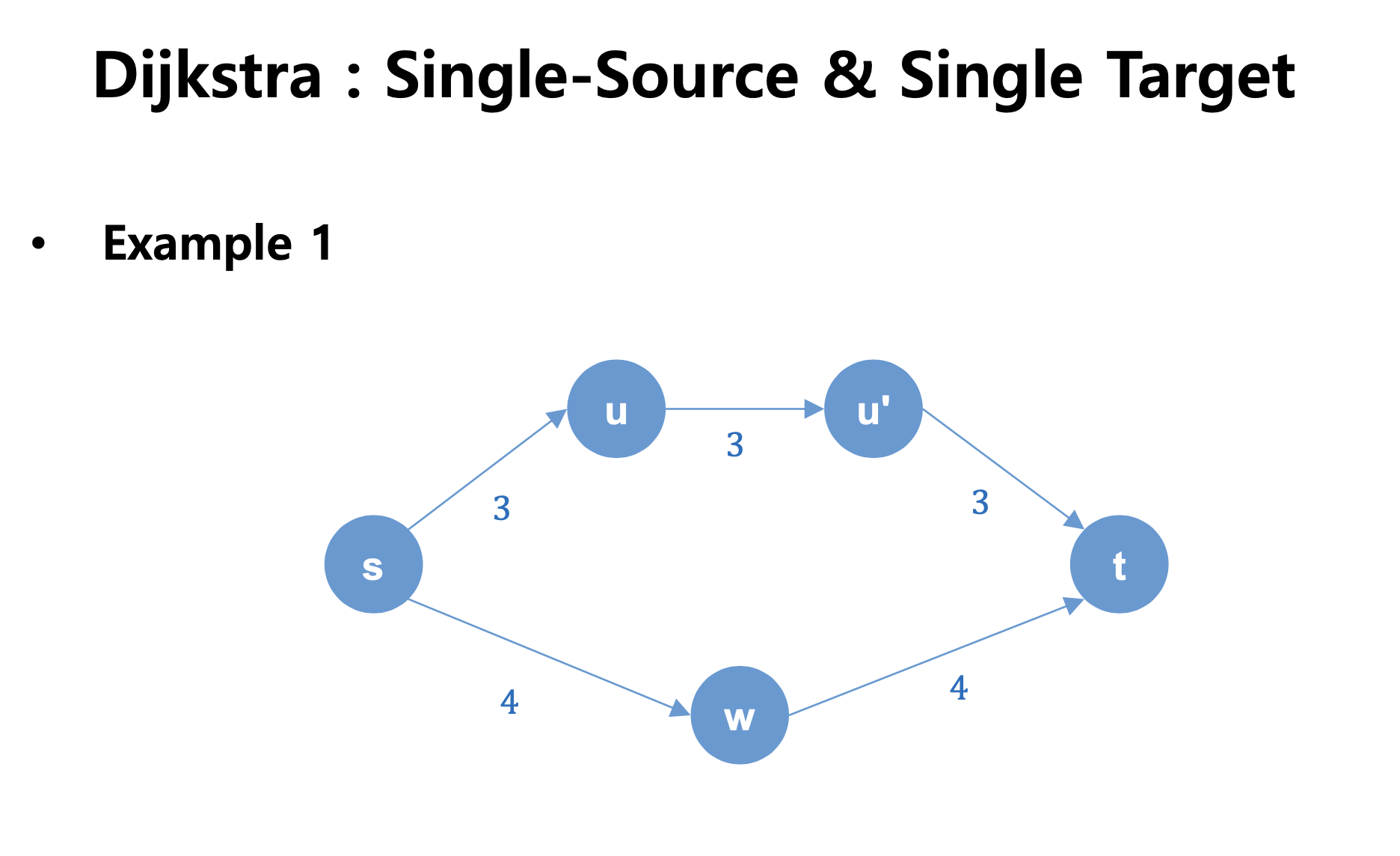
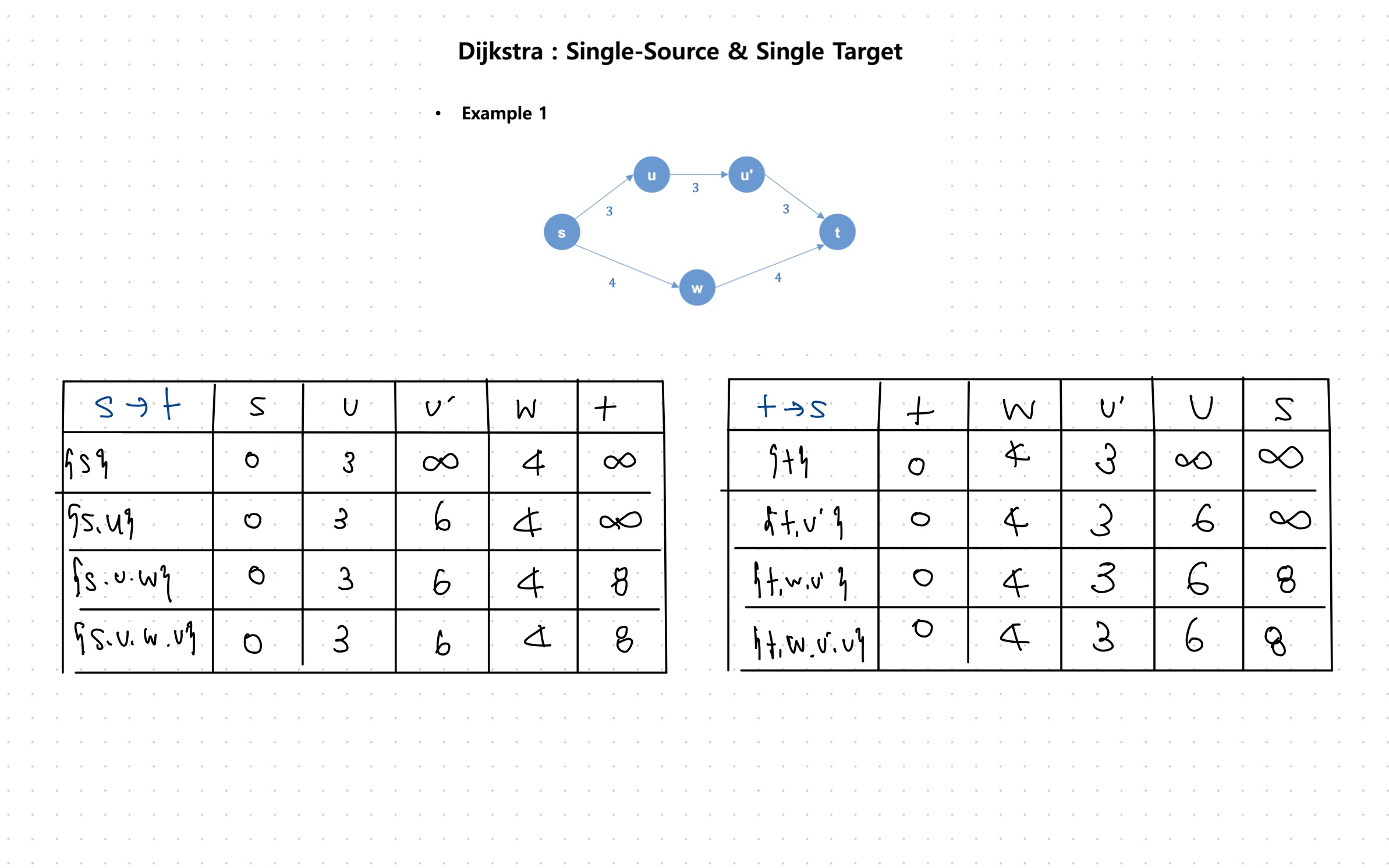
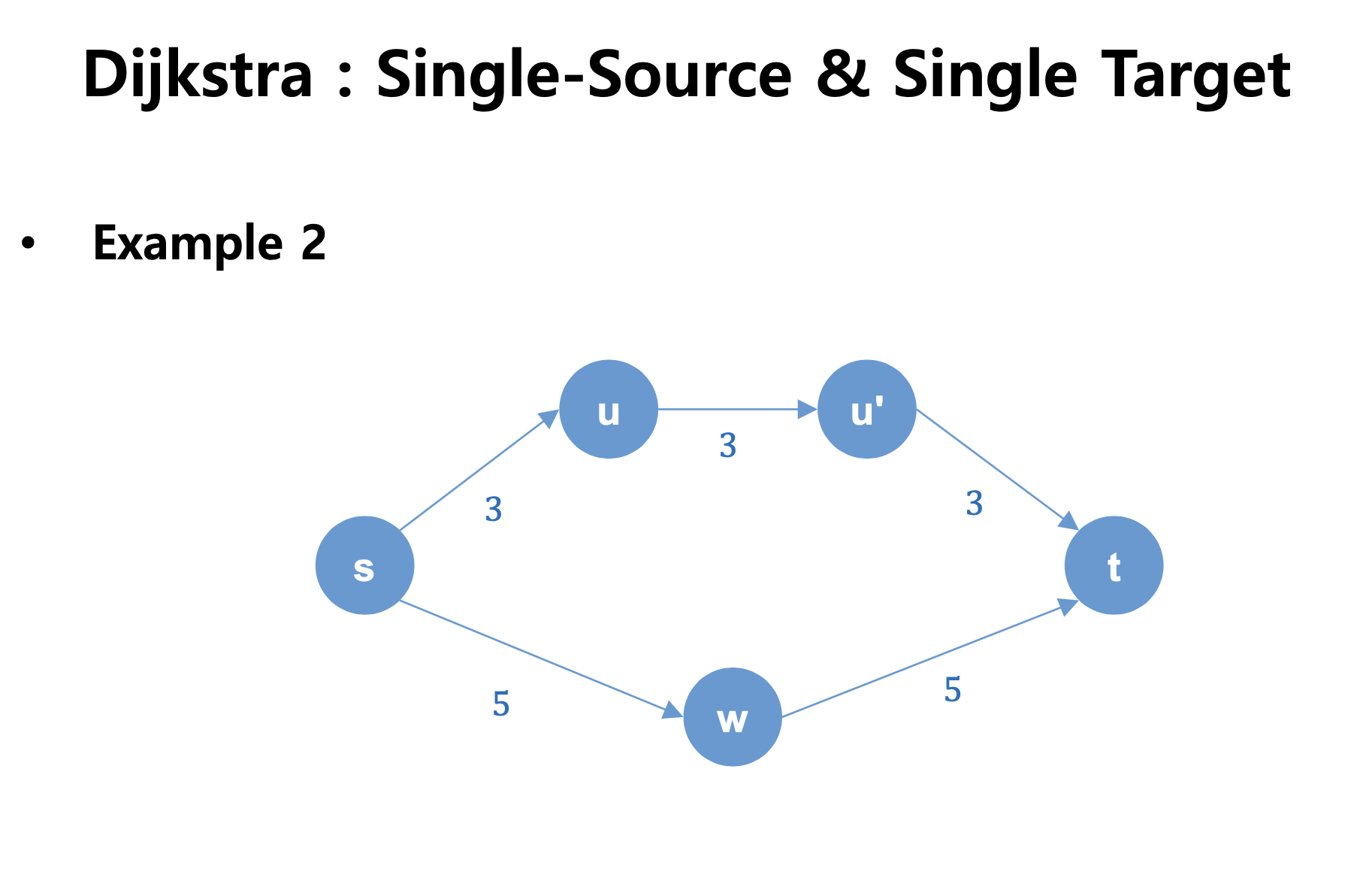
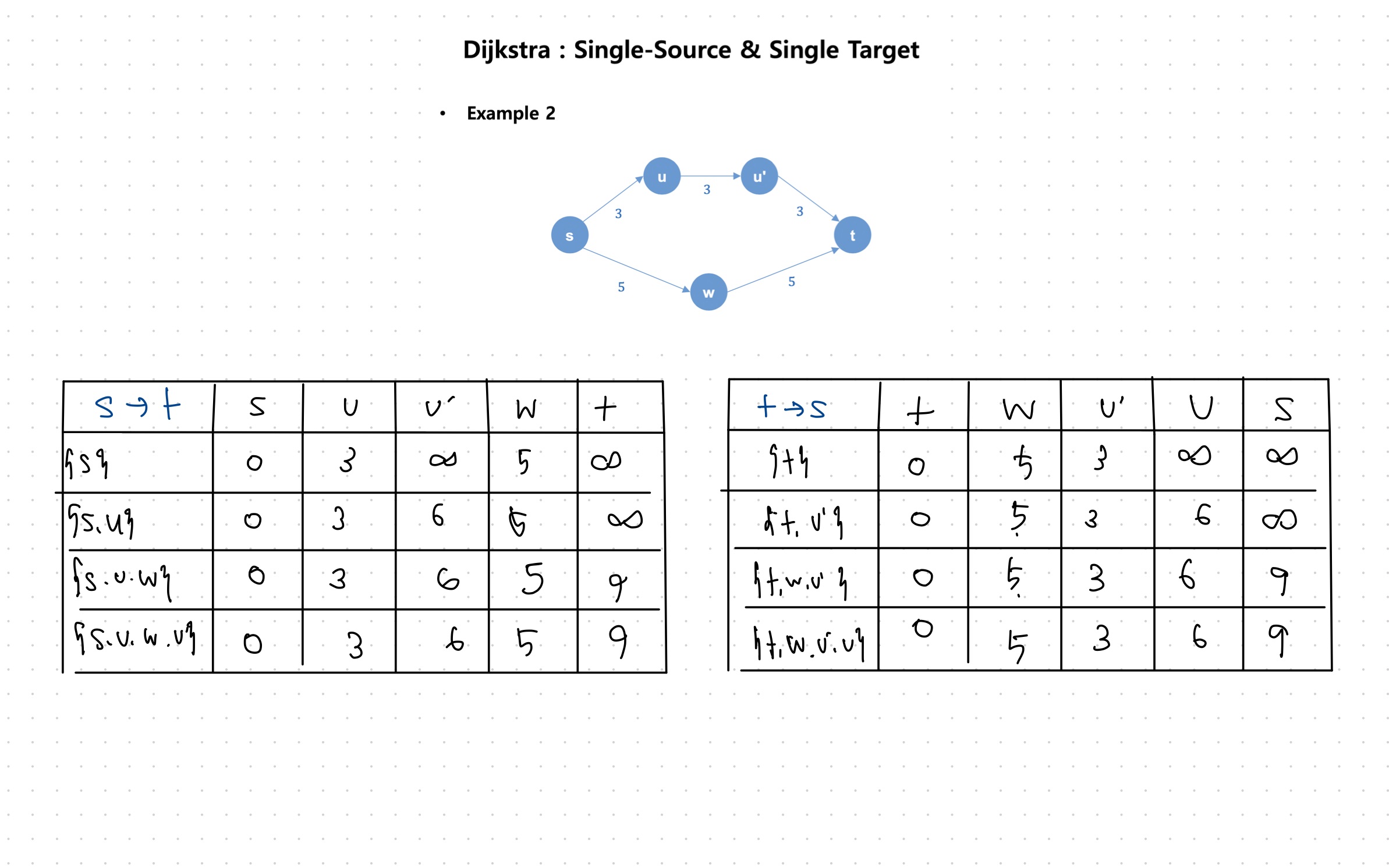
3. Refer to graph examples 1 and 2 on pages 21-22 of the class material titled 'Class material 06.pdf'. Given the graph, perform a Bi-Directional Search. The source vertex is 's', and the target vertex is 'D'. Draw the graphs for each step of your procedure.