알고리즘 Assignment 1

1. Manually determine the pairs of you who have the same birthday. Explain your method of solution.

1) 그룹의 생일을 모두 기록받아 하나씩 비교한다.
2) 모든 학생에게 임의의 숫자 번호(1~96)를 부여하고, 반복문을 통해 i번째 학생과 j번째 학생의 생일을 비교한다.

2. Develop an algorithm for the first question using pseudo code.

for i in range 95:
	for j in range(i+1, 96):
    	if (student[i] == student[j]):
        	print( "same birthday == ",i,"&",j)
 

3. Birthday Paradox
;100명의 학생이 있을 때, 그 중 생일이 같은 사람이 있을 확률은 99.999%임을 증명하기.

• Calculation Probability (확률 계산)
  n : 사람 수 (cf. 이때 1년은 365일이므로, n≥365로 가정한다.)
  p(n) : n 명의 사람이 모였을 때, 생일이 같은 사람이 둘 이상 있을 확률
  ~p(n) : n 명의 사람이 모였을 때, 모든 사람의 생일이 다를 확률 (~p(n)=1−p(n))
  -> 최종 구하고자 하는 사건 = *1-(365 Cnn!)/365^n**
  

def main():
    days = 365
    not_sharing = 1
    for i in range(1, days):
        probability = i / days
        not_sharing *= (1 - probability)
        result = 1 - not_sharing
        print("{0} - {1:.16f}".format(i + 1, result))


if __name__ == "__main__":
    main()

해당 코드를 통해 n명인 그룹에서, 생일이 같은 사람이 있을 확률을 계산할 수 있다.

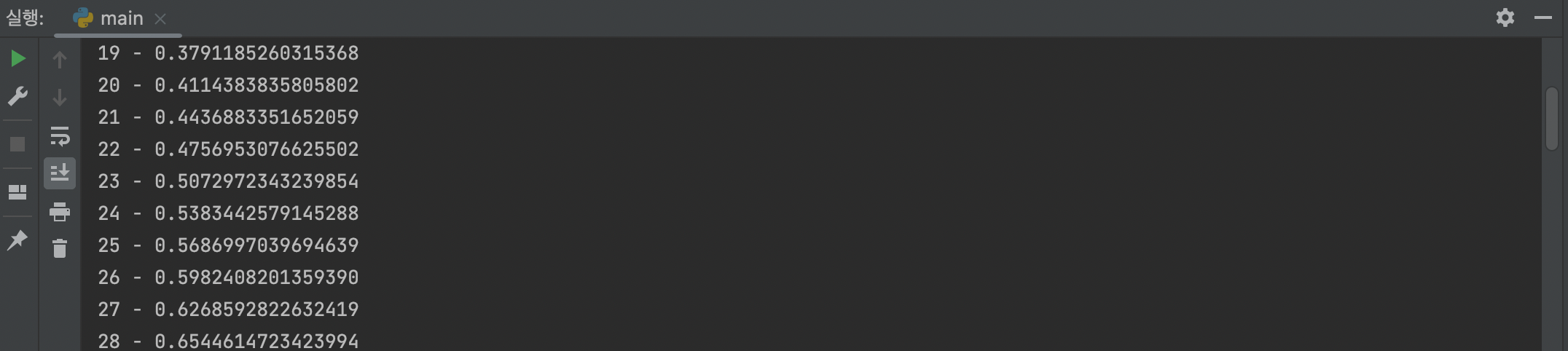
n=23 부터는 50%의 확률로 생일이 같은 사람이 존재한다는 것과

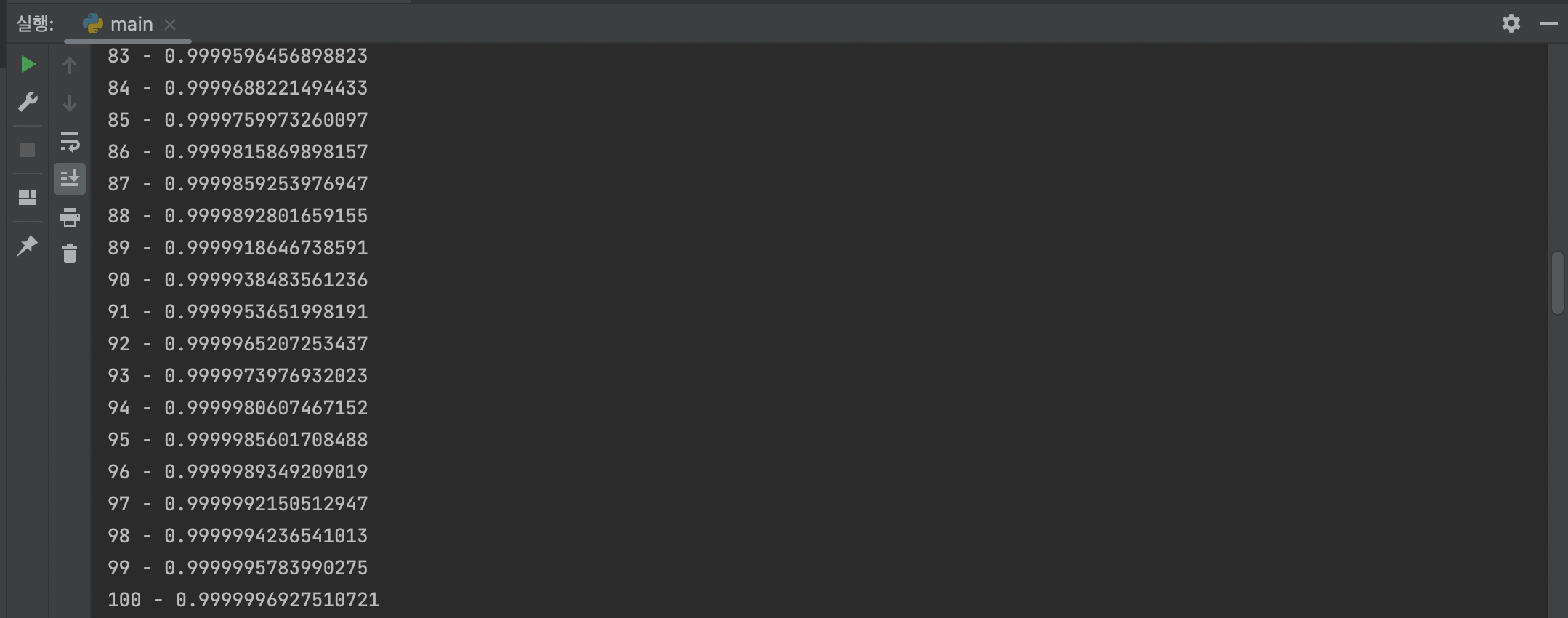
n=100인경우 99.999%로 생일이 같은 pair가 존재한다는 것을 확인할 수 있다.