Solve the problems 34 in chapter 1.
해당 루프문의 시간복잡도 T(n) 측정하기
What is the time complexity T(n) of the nested loops below?
For simplicity, you may assume that n is a power of 2.
That is, n = 2k for some positive integer k.
i =n ;
while ( i >= 1)
{
j =i ;
while ( j <= n)
{
< body o f the while loop> //Needs ( 1 ) .
j = 2 * j;
}
i = floor(i/2);
}▪️ 시간복잡도 Time Complexity
: 시간 복잡도는 연산의 개수를 세어 얼마만큼의 연산이 수행되는가를 통해 로직의 효율을 분석하는데 사용된다.
▪️ 시간복잡도의 종류
Big-O(빅-오) ⇒ 상한 점근 (wrost case)
Big-Ω(빅-오메가) ⇒ 하한 점근 (best case)
Big-θ(빅-세타) ⇒ 그 둘의 평균
위 세 가지 표기법은 시간 복잡도를 각각 최악, 최선, 중간(평균)의 경우에 대하여 나타내는 방법이다.
✔️ 빅오 표기법은 최악의 경우를 고려하므로, 프로그램이 실행되는 과정에서 소요되는 최악의 시간까지 고려할 수 있음.
▪️ 빅오 표기법의 종류 ( input size n )
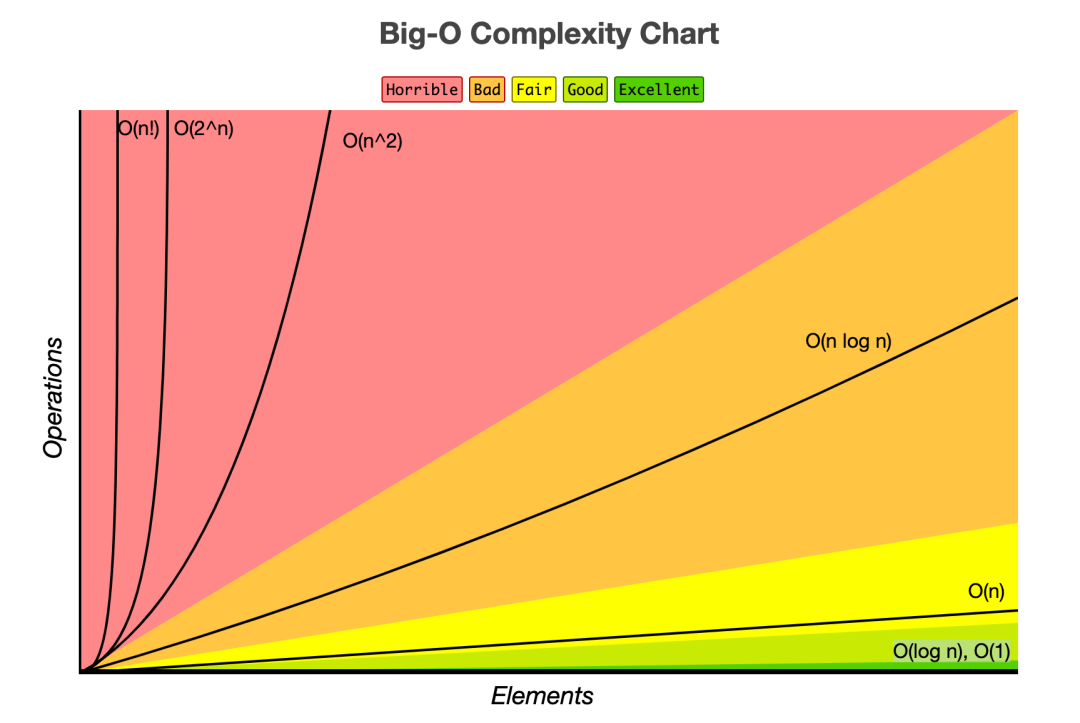
주로 nlgn, n, lgn 을 사용
▪️ 시간복잡도 계산
k=1, n=2 인 경우,
- i=2 > j=2 > j=4
- i=1 > j=1 > j=2 > j=4
(1+2)번 반복됨. (볼드: 내부 loop)
k=2, n=4 인 경우,
- i=4 > j=4 > j=8
- i=2 > j=2 > j=4 > j=8
- i=1 > j=1 > j=2 > j=4 > j=8
(1+2+3)번 반복됨.
위와 같이 1+2+..+(k+1)번 반복된다.
n=2^k 이므로 k=log^2 n
sum 공식을 통해
T(n)= (log^2 (n +1))*(log^2 (n))/2
따라서 시간복잡도가 O(log^2 n)라고 생각했다.
▪️ Solution과 비교
Solution: T(n) = (log2n + log n)/2 = O(log2n)
최종적인 답은 맞았는데
푸는 과정에서 차이가 있었던 것 같다.
아직 솔루션의 풀이과정을 이해하지 못했다.
Apply sorting algorithms to the birthday dataset.
Prove correctness of each algorithm
Argue efficiency of each algorithm
▪️ Permutation sort 순열정렬
def permutation_sort(A):
for B in permutations(A):
if is_sorted(B):
return B
순열 정렬은 메모리 낭비가 심하고 비효율적임.
▪️ Selction sort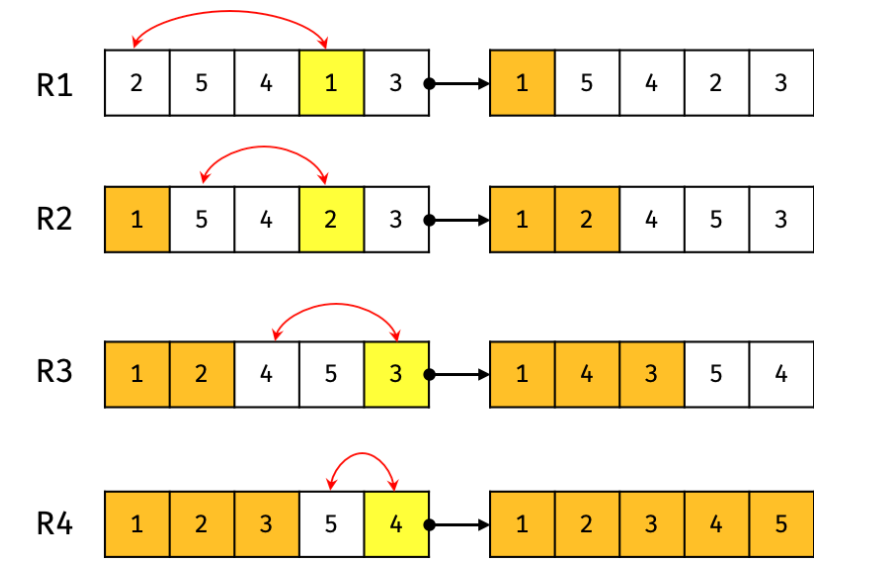
배열 A[1..n]에서 가장 큰 원소를 찾아 이 원소와 배열의 끝자리에 있는 A[n]과 자리를 바꾼다.
그러면 방금 맨 뒷자리로 옮긴 원소, 즉 가장 큰 원소는 자기 자리를 찾았으므로 더 이상 신경쓰지 않아도 되고, 이와 같은 방법으로 나머지 원소들의 작업을 반복하면 된다.
def selection_sort(A, i = None):
'''Sort A[:i+1]'''
if i is None : i=len(A)-1
j=prefix_max(A,i)
A[i],A[j]=A[j],A[i]
selection_sort(A,i-1)
