Hastad's Broadcast Attack

헌지박사·2023년 12월 16일

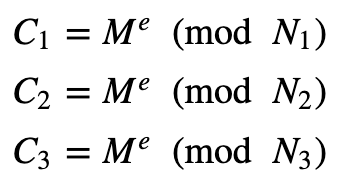
(※ Hastad's Broadcast Attack에 대한 증명은 생략하고 공격에 초점을 둔 게시글입니다.)

RSA 암호

RSA 암호 알고리즘 개요

RSA 암호는 인수분해의 어려움에 기초하고 있다.

어마어마하게 큰 소수(prime number) 두 개를 곱한다고 가정할 때, 둘을 곱하는 과정은 쉽지만, 해당 수를 둘을 인수분해하는 과정은 일반적으로는 매우 어렵다는 점을 생각하면 이해가 쉽겠다.

타인에게 노출되는 Public key 의 경우 (n,e) 쌍인데, 모든 사용자가 사용할 수 있으며, 평문을 암호화할 때 사용한다.

개인만 가지고 있는 Private key 의 경우 타인에게 노출되어서는 안되며, 공개키로 암호화된 암호문을 복호화할 때 사용한다.

RSA 암호는 "오일러 정리" 가 중추적인 역할을 하고 있으므로, 반드시 짚고 넘어가야 RSA 암호 알고리즘에 관한 이해를 할 수 있다.

오일러 정리

$n$ 과 서로소인 양의 정수 $m$ 이 있을 때, 다음 식을 만족한다.

$m^{\phi(n)}\equiv 1\pmod n$

여기서 $\phi(n)$ 는 n과 서로소인 수의 개수를 나타낸다 (단, n보다 작아야 함). 해당 함수를 오일러 파이 함수(Euler's phi function)라고 부르며, 만약

$n = p \times q$ (단, p, q는 소수)

의 조건을 만족한다면, $\phi(n)$ 은 $n$ 보다 작으면서 $p$ 와 $q$ 의 배수가 아닌 수들의 개수가 되므로,

$\phi(n) = pq - p - q + 1 = (p-1)(q-1)$

처럼 수식으로 나타낼 수 있다.

참고로 임의의 소수 $p$ 에 대하여, $\phi(p^k)$ 꼴로 오일러 파이함수가 나오면 $p$ 만을 소인수로 가지기 때문에

$\phi(p^k) = p^k - p^{k-1} = p^{k-1}(p-1)$

꼴로 나타낼 수 있다.

키 생성

(1) 우선 1024bit 이상의 서로 다른 두 소수 $p, q$ 를 선택한다. 그 뒤, $p, q$ 를 곱하여 $N$ 을 구하고, $\phi(N)$ 를 계산한다. 위에서 언급한 바와 같이 $\phi(N)$ 은 두 소수의 곱으로 이루어져 있으므로 다음과 같은 수식으로 나타낼 수 있다.

$\phi(n) = pq - p - q + 1 = (p-1)(q-1)$

(2) $\phi(N)$ 을 구했다면, $\phi(N)$ 과 서로소인 $e$ 를 선택한다. 일반적으로 $e$ 의 값은 너무 크면 효율성이 떨어지게 되고, 너무 작으면 Coppersmith's Short Pad Attack, Hastad's Broadcast Attack 등에 취약해지므로, $2^{16}+1=65537$ 을 선택한다.

(3) 그 다음으로는 $d\equiv e^{-1}\mod N$ 인 $d$ 를 구한다.

(4) $(N,e)$ 쌍은 공개키로, $d$ 는 개인키로 활용된다.
여기서 생성된 $N$ 은 modulus, $e$ 는 public exponent, $d$ 는 private exponent 라고 부른다.

암호화

공개키 $(N,e)$ 로 $n$ 보다 작은 평문 $m$ 을 암호화할 때, 암호문 $c$ 는 다음 식으로 구할 수 있다.

$c\equiv m^e\pmod N$

복호화

위에서 구한 $c$ 를 개인키 $d$ 로 복호화할 때, 평문 $m$ 은 다음과 같이 구할 수 있다.

$m\equiv c^d\pmod N$
$c^d\equiv(m^e)^d\equiv m^{ed} \pmod N$

오일러 정리로 $e,d$ 값을 서로 곱했을 때 $ed = k\phi(N) +1$ 이므로, 복호화 방식은 쉽게 확인할 수 있다.

$m^{ed}\equiv (m^\phi(N) )^km \pmod N\equiv m\pmod N$

작은 수로 예를 들어,

$p = 11,\ q = 3,\ n = 33,\ \phi(N) = 20,\ e=3,\ d= 7$

로 가정했을 때, plaintext 인 $M=15$ 를 암호화 하고자 한다.

암호문은 $C = 15^3 \mod 33 = 9$ 로 구할 수 있고, 해당 암호문 $C$ 의 평문은, $M = 9^7 \mod 33 = 15$ 로 구할 수 있다.

Hastad's Broadcast Attack

Hastad's Broadcast Attack 개요

해당 포스팅의 메인 주제인 Hastad's Broadcast Attack은 다수의 수신자에게 동일한 평문을 동일하고 작은 public exponent인 $e$ 로 암호화한 뒤 전송할 때, 각자의 modulus인 $N_1,N_2,N_3$ 가 서로소라면, 유효한 공격이다.

해당 공격은 CRT(Chinese Remainder Theorem)를 이용한다.

CRT(Chinese Remainder Theorem)

중국인의 나머지 정리라고도 부르는 CRT는 자연수 $a_1,N_1,a_2,N_2,...,a_k,N_k$ 가 주어졌을 때, 연립합동식

$x\equiv a_i \pmod{N_i}\ \ \ \ \ \ \ i=1,2,...k$

를 푸는 문제이다.

$N_i$ 쌍 들의 값이 서로소라면, $x\equiv C \pmod {N_1N_2...N_k}$ 를 만족하는 유일한 해 $C$ 가 있다는 것이 그 내용이다.

Hastad's Broadcast Attack

A, B, C 가 RSA 암호를 통해서 통신한다고 가정하자. 단, 이 때의 $e$ 값은 충분히 작은 값인 3, $N$ 값은 각자 다르고 서로소인 modulus( $N_1,N_2,N_3$ ) 로 통신한다.
각자의 암호문은 다음과 같은 수식을 만족시킬 것이다.

A: $x \equiv C_1 \pmod {N_1}$
B: $x \equiv C_2 \pmod {N_2}$
C: $x \equiv C_3 \pmod {N_3}$

이 때 CRT 를 적용하면 다음을 만족하는 해( $x$ )도 존재한다.

$x \equiv P^3 \pmod {N_1N_2N_3}$

우리가 구한 해는 CRT에 의해서 $N_1,N_2,N_3$ 에 대한 나머지 조건도 모두 만족한다. 즉, $x \equiv P^3 \pmod {N_1}$ 와 $x \equiv P^3 \pmod {N_2}$ 그리고 $x \equiv P^3 \pmod {N_3}$ 를 만족하는 해이다. $P<N_1, P<N_2, P<N_3$ 을 만족하므로 $P^3<N_1N_2N_3$ 이므로 $P^3= x$ 를 만족하여, $x$ 의 세제곱근을 단순하게 구하는 것으로 RSA 암호는 깨진다.

공격 실습

백문이 불여일견이라 했으니 실습을 해보도록 하자. 우선, 다음과 같이 간단히 textbook-RSA 암호를 만들어보자. 일부러 취약하게 만들기 위해서 public exponent( $e$ ) 값은 3으로 설정한다.

#!/usr/bin/env python3
from Crypto.Util.number import *

p1 = getStrongPrime(512)
q1 = getStrongPrime(512)
p2 = getStrongPrime(512)
q2 = getStrongPrime(512)
p3 = getStrongPrime(512)
q3 = getStrongPrime(512)

N1 = p1 * q1
N2 = p2 * q2
N3 = p3 * q3
e = 3

pt = bytes_to_long(b"Flag{Hastad's Broadcast Attack! It is based on CRT(Chinese Remainder Theorem)! Can you crack it?}")
C1 = pow(pt, e, N1)
C2 = pow(pt, e, N2)
C3 = pow(pt, e, N3)

print(f"A said, N1={N1}, C1={C1}")
print(f"B said, N2={N2}, C2={C2}")
print(f"C said, N3={N3}, C3={C3}")

그러면 다음과 같이 출력값이 나온다.

A said, N1=137412680804369570491122530311395962213888803113667102635828321941443830825508726641739026471143891698001545240544961564817671064515549308064787263248737373352099072668355711100267457866984988258257780546135270471612949090050236940772583358126803475848228992474466231218465829039783033421583622467430665484989, C1=82152838166558180963289143906419525570357824024979138106801061598704871766991401965964164725758246670208967861921747995138698306252179026259579048549544400206153268744614962606307174612831342923017354764451560137024564099416223356015282597756364815704124460730795827212664771681906635589848820381777870854436
B said, N2=133163760244918375509881472916000055487739900262502333310149759502209656077745069473496291567068252746189524293392341167361299393110127277911654464596983506118347383091688882173660751643151344048284418420498141602607022988199982838557963496700403388899410349907483453960109742198281359267977446643933444069161, C2=31738004654900388774198799852253962692992718487479942963868322803454739516908148204639873728882108319141791268567283783252802509599110142601020366681926624907938748126983413578987141272300268956001105164224017945299261171127132761095682338494348379819927262827323777096921594360184137796948163338783271557731
C said, N3=135162648317498798564112984607884159108816052249457232939273578478560195616243827026688458802678306703986363827647854522210112139449671548602267662102492770414586455733828631327187612560565712063969404958636274879496013022348494378819904420579540569991736014895125476505372096974753839498467035337295630088153, C3=9194967439841934065527724556617316647098628912886509439463481954786212121260137086848571269904816281018914614936759327588837787756269338068056126643570060897632621913561275531003994835472830962631091812594810033563768898204294165626888943743433793077648925234800721479298378765893947954372351465873642268741

Hastad's Broadcast Attack을 할 때, CRT 알고리즘은 다음과 같이 짤 수 있다.(출처: https://docs.xanhacks.xyz/crypto/rsa/08-hastad-broadcast-attack/)

from gmpy2 import invert


def mul(lst):
    ret = 1
    for n in lst:
        ret *= n
    return ret

def crt(C, N):
    assert len(C) == len(N)

    total = 0
    modulo = mul(N)

    for n_i, c_i in zip(N, C):
        p = modulo // n_i
        total += c_i * invert(p, n_i) * p
    return total % modulo

libnum에 crt 함수가 구현되어 있다. 풀이는 libnum에서 solve_crt를 호출해서 하도록 하겠다.

from Crypto.Util.number import *
from gmpy2 import *
from libnum import *

c = [82152838166558180963289143906419525570357824024979138106801061598704871766991401965964164725758246670208967861921747995138698306252179026259579048549544400206153268744614962606307174612831342923017354764451560137024564099416223356015282597756364815704124460730795827212664771681906635589848820381777870854436, 31738004654900388774198799852253962692992718487479942963868322803454739516908148204639873728882108319141791268567283783252802509599110142601020366681926624907938748126983413578987141272300268956001105164224017945299261171127132761095682338494348379819927262827323777096921594360184137796948163338783271557731, 9194967439841934065527724556617316647098628912886509439463481954786212121260137086848571269904816281018914614936759327588837787756269338068056126643570060897632621913561275531003994835472830962631091812594810033563768898204294165626888943743433793077648925234800721479298378765893947954372351465873642268741]
N = [137412680804369570491122530311395962213888803113667102635828321941443830825508726641739026471143891698001545240544961564817671064515549308064787263248737373352099072668355711100267457866984988258257780546135270471612949090050236940772583358126803475848228992474466231218465829039783033421583622467430665484989, 133163760244918375509881472916000055487739900262502333310149759502209656077745069473496291567068252746189524293392341167361299393110127277911654464596983506118347383091688882173660751643151344048284418420498141602607022988199982838557963496700403388899410349907483453960109742198281359267977446643933444069161, 135162648317498798564112984607884159108816052249457232939273578478560195616243827026688458802678306703986363827647854522210112139449671548602267662102492770414586455733828631327187612560565712063969404958636274879496013022348494378819904420579540569991736014895125476505372096974753839498467035337295630088153]
# libnum.solve_crt
m_3 = solve_crt(c,N)
m = int(iroot(m_3,3)[0])
print(long_to_bytes(m))

위 python 코드를 실행하게 되면, libnum의 solve_crt 함수로 $m^e$ 값을 구하게 되고, $e$ 값은 3이므로 iroot를 이용해서 세제곱근을 구하게 되면, 손쉽게 구할 수 있다.

iroot가 아닌 단순 1/3 제곱을 해주면 값이 길어서 짤릴 수도 있으니 libnum같은 모듈을 불러서 사용하도록 하자 ( 암호학 관련해서 평소 참고하던 블로그에서 1/3 제곱(**(1/3))으로 하니 암호문이 짤렸다는 후기를 본 적이 있다. ).

python 코드 실행 이후 다음과 같이 RSA 암호가 깨진 것을 확인할 수 있다.

대처 방안

당연하게도 작은 public exponent( $e$ ) 값을 사용하면 안된다. 작은 $e$ 값을 사용하게 되면, Hastad's Broadcast Attack 뿐 아니라, CopperSmith's Short Pad Attack에도 취약해질 수 있다. public exponent( $e$ ) 값은 위에도 언급한 바와 같이 $2^{16}+1$ 인 65537이 적당하다.