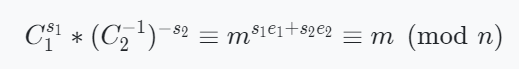
---

(※ 기본적인 RSA 암호 알고리즘에 대한 이해가 필요한 게시글입니다.)
(1. RSA 암호 알고리즘과 Hastad's Broadcast Attack)

Common Modulus Attack

RSA 암호를 사용하면서 $n(=p\times q)$ 값을 재사용하는 경우가 생길 수 있다. 여기서 $e$값을 권고값이 아닌 다양한 값으로 바꿔가면서 사용하는 경우, Common Modulus Attack에 취약해진다.

선행 조건

$N_1=N_2$일 때, $e_1,c_1,e_2,c_2$값이(public exponent와 ciphertext) 가 필수적으로 주어져야 한다.

이 때 다음과 같은 조건이 성립하면 Common Modulus Attack을 수행할 수 있다.

$\gcd(e_1,e_2) = 1$
$\gcd(c_2,n) = 1$

해당 조건들이 성립해야 하는 이유는 간단하다 Common Modulus Attack을 수행하려면,
1. $c_2$는 $n$에 대한 모듈러 역원($C_2^{-1}\pmod n$)을 구해야 하고,
2. 베주 항등식에 의하면 $se_1 + te_2 = \gcd(e_1,e_2)$ 를 만족하는 정수 쌍 $s,t$가 반드시 존재하고, 뒤의 값이 1이 나오려면 public exponent ($e_1, e_2$) 끼리는 서로소여야 하기 때문이다.

수학적 배경

RSA 암호화가 다음과 같다는 점은 앞선 포스팅을 보고 오면 당연한 사실이다.

$c = m^e \pmod n$

위에서 언급한 선행 조건들에 의해 $e_1, e_2$는 서로소이다. 따라서 베주 항등식 을 적용하면 우리는 다음과 같은 방정식을 얻을 수 있다.

$xe_1 + ye_2 = \gcd(e_1,e_2)=1$

이를 이용하면, 우리는 평문 $m$을 유도해낼 수 있다.
모든 계산은 $\mod n$ 처리한 것으로 간주.

$C_1^x * C_2^y = (m^{e_1})^x *(m^{e_2})^y = m^{e_1x+e_2y}=m^1 = m$

일반적으로, 베주 항등식은 양수와 음수 쌍이 나온다(참조: https://cryptohack.gitbook.io/cryptobook/untitled/common-modulus-attack). 우리는 해당 방정식을 우리가 쓸 수 있도록 약간만 수정해주면 된다. 일단 $y$가 음수라고 가정을 하고 시작해보자.

$Let\space y = -a$
$C_2^y = C_2^{-a}$
$=(C_2^{-1})^a$
$=(C_2^{-1})^{-y}$

이제 평문을 해독하기 위해서, 우리는 다음을 수행하면 된다.

$C_1^x \times (C_2^{-1})^{-y} \pmod n$

결국 위에서 언급한 식에 의해서 $m$ 평문이 유도가 된다.

공격 실습

$n$값을 공유하는 간단한 textbook-RSA 암호 두개를 만들어보자.

from Crypto.Util.number import *

p = getStrongPrime(1024)
q = getStrongPrime(1024)

#common modulus
N = p * q
e1 = 26107
e2 = 8191

pt = bytes_to_long(b"Flag{Common Modulus Attack! Do not modify the public exponent!}")
C1 = pow(pt, e1, N)
C2 = pow(pt, e2, N)

print(f"A said, N={N}, e1={e1}, C1={C1}")
print(f"B said, N={N}, e2={e2}, C2={C2}")

그러면 다음과 같이 값이 나온다.

A said, N=25142409503153206358726147968951147534219474744294747586481943203086791669446895347058351206138383194361749861284670768660229615209606464811701601902643068125147362684649279755160399746739928765274780537388834706037077953668755767338541055597129895350604779226874293302656993424374458564535061675945072226494077110700133751938808151373310329364999496482737018966066613620298698563872652932450107873159005160300050648153765640788527121416876894243799134214468289490365850752857830897670474744335332009287010549365526520204590649079997345252599473911156067135672457575141473204884592400485421903592898177620581089454079, e1=26107, C1=12404765707330526191953002366654178087800137984328434621467453868938303632944535448425774454715994818366690724384919087307384142058368014736986430763992436534170867512896094790736859490484496293958580633581468978591449481692869985194861502204515640705037633050537931408941888317058352585802011650417741263987026809590913928188611146226721954238242076210586717768330620946075163472528448487790607526778384017312655017988107415182098580741503284344634550660396531023806977072373441657103581599544933792730827526678213110332513916696829201230671301685482028115374142280916439296828305222027635406027242124718570380279530
B said, N=25142409503153206358726147968951147534219474744294747586481943203086791669446895347058351206138383194361749861284670768660229615209606464811701601902643068125147362684649279755160399746739928765274780537388834706037077953668755767338541055597129895350604779226874293302656993424374458564535061675945072226494077110700133751938808151373310329364999496482737018966066613620298698563872652932450107873159005160300050648153765640788527121416876894243799134214468289490365850752857830897670474744335332009287010549365526520204590649079997345252599473911156067135672457575141473204884592400485421903592898177620581089454079, e2=8191, C2=14622946914123594128912986383319563039359781040509418637425032573792423411004881985749781237499550253753313310949141624873239127949318613335134586413991845585048918926044506414641022210379131948208629235411831906202695003007804959963170133031045136116901330759588275208587781576066961808398608837714029246066394909138978876389158718606651156461750593330485831546133367110951858305987574730351595877121250504230437286693355771005581193933880441236821456517462206082465560840732897491716327428654186821599321078818132730794487906248362004464514249250259897831447884166532388538955201124161981817083402163058976096300061

Common Modulus Attack의 경우 공격 코드를 매우 쉽게 짤 수 있다.
방정식을 $s_1e_1+s_2e_2 = 1$ 로 가정한 뒤, $s_2$값을 음수로 취급하도록 정한다. 나머지 양수로 가정한 $e_1$의 $\mod e_2$에 대한 역원을 구하여 $s_1$값을 구해준다(이해가 안된다면 확장 유클리드 알고리즘을 한 번 알아보자).

($s_1 = e_1^{-1}\pmod {e_2}$).

$s_2$의 값은 $\frac{(1-s_1e_1)}{e2}$ 일 것이므로(정확히는 1 은 $\gcd(e_1,e_2)$이다 - 베주항등식 참조.), 해당 코드를 구성하면 $s_1, s_2$ 모두 구할 수 있다.

즉,

$s_1 = e_1^{-1}\mod e_2$
$s_2 = \frac{(\gcd (e_1,e_2) - e_1s_1)}{e_2}$

위에서 언급한 식($C_1^x * C_2^y = (m^{e_1})^x *(m^{e_2})^y = m^{e_1x+e_2y}=m^1 = m$, mod연산 생략)에서 $x$는 $s_1$ 에 해당되고, $y$는 $s_2$에 해당된다.

즉, 마지막으로 다음 처리를 하면 평문 $m$을 유도해낼 수 있다.

$C_1^{s_1}*(C_2^{-1})^{-s_2}\equiv m^{s_1e_1+s_2e_2}\equiv m \pmod n$

위를 바탕으로 평문 $m$을 구하는 알고리즘은 간단하게 다음과 같이 구현할 수 있을 것이다.

s1 = inverse(e1, e2)
s2 = (gcd(e1, e2) - e1*s1)//e2
temp = inverse(ct2, n)
m1 = pow(ct1, s1, n)
m2 = pow(temp, -s2, n)

print(long_to_bytes((m1*m2) % n))

만약, assert 기능으로 $n_1, n_2$값이 서로 같은지, $e_1,e_2$가 서로소인지, $C_2,n_1$가 서로소인지, 공격 수행 전에 검사하는 기능을 추가한다면 다음과 같이 코드를 구성할 수 있을 것이다(참고: https://infosecwriteups.com/rsa-attacks-common-modulus-7bdb34f331a5).

from Crypto.PublicKey import RSA
from Crypto.Util.number import long_to_bytes, bytes_to_long, GCD as gcd, inverse

e1 = 26107
e2 = 8191
n1 = 25142409503153206358726147968951147534219474744294747586481943203086791669446895347058351206138383194361749861284670768660229615209606464811701601902643068125147362684649279755160399746739928765274780537388834706037077953668755767338541055597129895350604779226874293302656993424374458564535061675945072226494077110700133751938808151373310329364999496482737018966066613620298698563872652932450107873159005160300050648153765640788527121416876894243799134214468289490365850752857830897670474744335332009287010549365526520204590649079997345252599473911156067135672457575141473204884592400485421903592898177620581089454079
n2 = 25142409503153206358726147968951147534219474744294747586481943203086791669446895347058351206138383194361749861284670768660229615209606464811701601902643068125147362684649279755160399746739928765274780537388834706037077953668755767338541055597129895350604779226874293302656993424374458564535061675945072226494077110700133751938808151373310329364999496482737018966066613620298698563872652932450107873159005160300050648153765640788527121416876894243799134214468289490365850752857830897670474744335332009287010549365526520204590649079997345252599473911156067135672457575141473204884592400485421903592898177620581089454079
ct1 = 12404765707330526191953002366654178087800137984328434621467453868938303632944535448425774454715994818366690724384919087307384142058368014736986430763992436534170867512896094790736859490484496293958580633581468978591449481692869985194861502204515640705037633050537931408941888317058352585802011650417741263987026809590913928188611146226721954238242076210586717768330620946075163472528448487790607526778384017312655017988107415182098580741503284344634550660396531023806977072373441657103581599544933792730827526678213110332513916696829201230671301685482028115374142280916439296828305222027635406027242124718570380279530
ct2 = 14622946914123594128912986383319563039359781040509418637425032573792423411004881985749781237499550253753313310949141624873239127949318613335134586413991845585048918926044506414641022210379131948208629235411831906202695003007804959963170133031045136116901330759588275208587781576066961808398608837714029246066394909138978876389158718606651156461750593330485831546133367110951858305987574730351595877121250504230437286693355771005581193933880441236821456517462206082465560840732897491716327428654186821599321078818132730794487906248362004464514249250259897831447884166532388538955201124161981817083402163058976096300061

assert n1 == n2
assert gcd(e1, e2) == 1
assert gcd(ct2, n1) == 1 # both steps confirm we can use common modulus attack

n = n1

# attack part

s1 = inverse(e1, e2)
s2 = (gcd(e1, e2) - e1*s1)//e2
temp = inverse(ct2, n)
m1 = pow(ct1, s1, n)
m2 = pow(temp, -s2, n)

print(long_to_bytes((m1*m2) % n))

해당 코드를 실행하면, Common Modulus Attack으로 평문($m$)을 해독할 수 있다.

대처 방안

이 방법 때문에 공개키에 조건을 다는 것이 아닌, $2^{16}+1 = 65537$ 고정값으로 권고하는 것이라고 한다(출처: https://librewiki.net/wiki/RSA). 만약, 동일 암호시스템에서 공개키가 서로 다른 경우가 발생한다면, 동일 $n$값을 사용하는 암호에서 Common Modulus Attack 이 가능할 수도 있다.

---

출처: https://cryptohack.gitbook.io/cryptobook/untitled/common-modulus-attack
https://en.wikipedia.org/wiki/B%C3%A9zout%27s_identity
https://infosecwriteups.com/rsa-attacks-common-modulus-7bdb34f331a5
https://www.math.umd.edu/~immortal/MATH406/lecturenotes/ch8-Additional.pdf
https://librewiki.net/wiki/RSA
https://en.wikipedia.org/wiki/Extended_Euclidean_algorithm