최단경로 알고리즘 (길찾기)
특정 지점에서 특정 지점까지 가기 위한 최단 경로를 구하기 위한 알고리즘

경로 계산 방식에도 종류가 있음
1. One-To-One : 한 지점에서 다른 특정 지점까지의 최단경로 구하기
2. One-To-All : 한 지점에서 다른 모든 지점까지의 최단경로 구하기 (Dijksta)
3. All-To-All : 모든 지점에서 다른 모든 지점까지의 최단경로 구하기

다익스트라

그래프에서 특정 노드에서 출발해 다른 모든 노드로 가는 각각의 최단 경로를 구해주는 알고리즘이다.

모든 간선의 가중치(길이)는 양의 정수 값 일 것

동작 방식

1. 출발 노드를 설정, 최단 거리 테이블을 초기화
2. 방문하지 않은 노드 중 최단 거리가 가장 짧은 노드 선택
3. 해당 노드를 거쳐 다른 노드로 가는 비용을 계산해 최단 거리 테이블 갱신
   • 갱신 : 현재 테이블의 최단거리보다, 해당 노드를 거쳐가는 비용이 작으면 작은 경로로 교체
4. 3~4 과정을 반복

예시 1

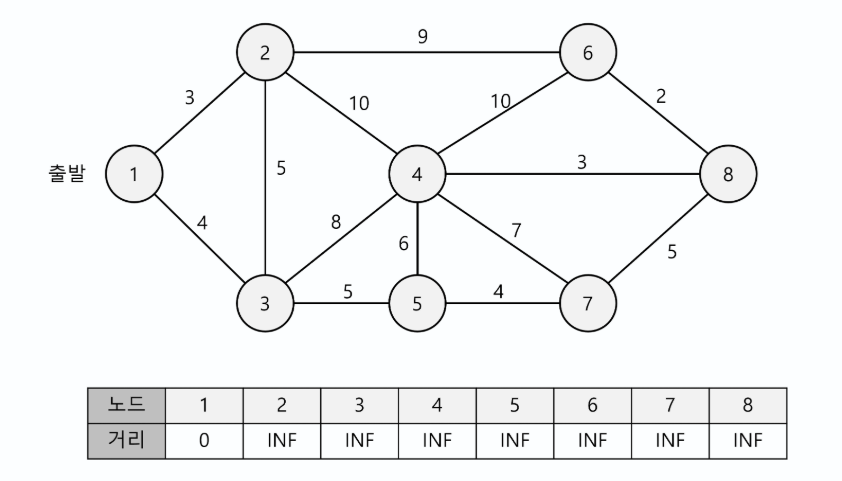
최단거리 테이블은 각 노드에 대해 주어지며, 각 값들은1번 노드에서 $X$번 노드로 가는 최단 경로를 의미한다.
처음에는 1번 노드에서 자기 자신의 거리는 0이고, 나머지는 $\infty$(무한)값으로 초기화한다.

1. 출발인 1번 노드를 선택하고, 해당노드를 거쳐 갈 수있는 다른 노드들(2번,3번)의 거리를 계산하여 갱신한다.(무한 값보다 작으므로 갱신된다.)

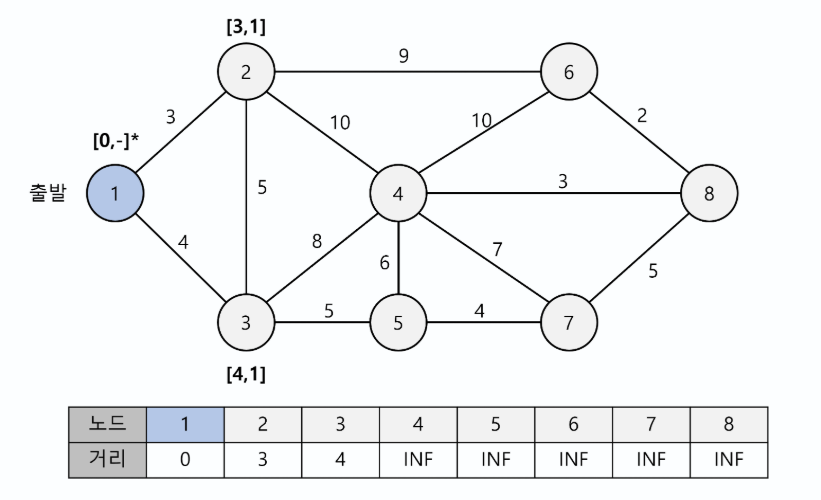
노드 위의 식별값은 [최단거리, 이전노드]로 표현되며 방문한 적이 있는 노드는 더 이상 갱신할 필요가 없어 *로 표시한다.

2. 방문하지 않은 노드 중 가장 짧은 최단거리 노드(2번)을 선택하고 해당 노드를 거쳐갈 수 있는 다른 노드의 최단 거리 값을 갱신한다.

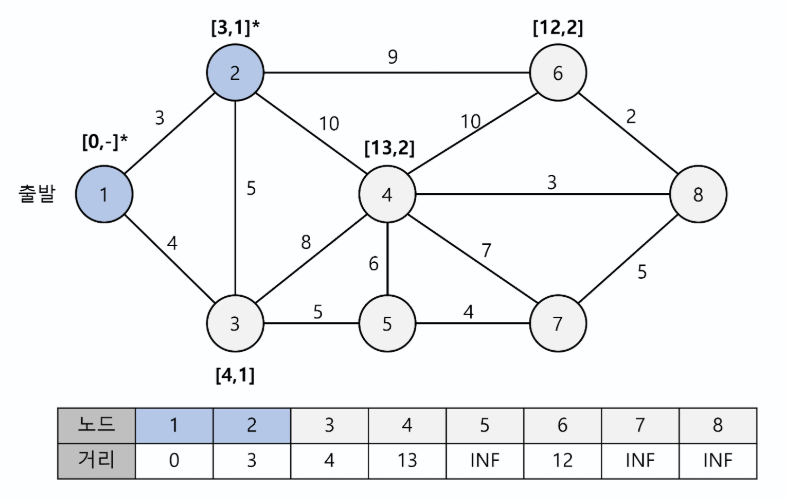
3. 마찬가지로 3번 노드를 선택하여 반복

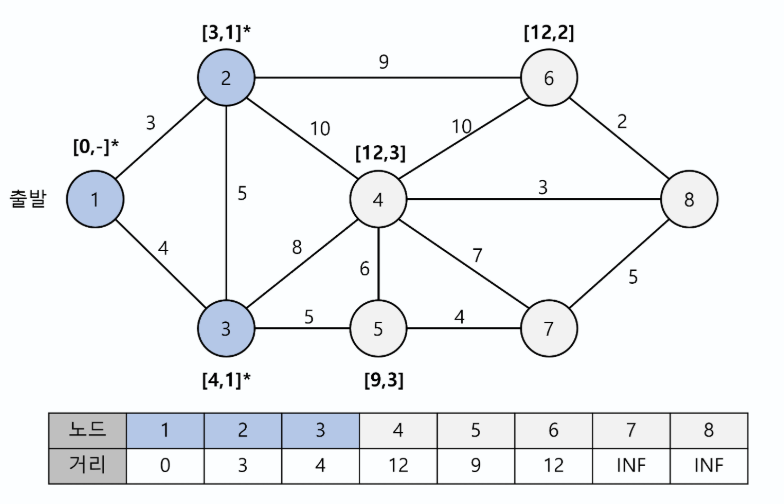
4. 여기서 중요한 점은 4번 노드의 최단거리가 2번 노드에 의해 13이었는데 이번 단계에서 3번 노드에 의해 12로 갱신 된다는 것이다.
   즉, 다익스트라가 One-To-All방식이므로 모든 경로 탐색이 끝날때까지 목적지 최단 거리를 알기 어렵다.

• 이 과정을 계속 반복하면 아래와 같은 결과와 최단거리 테이블을 얻을 수 있다.
  

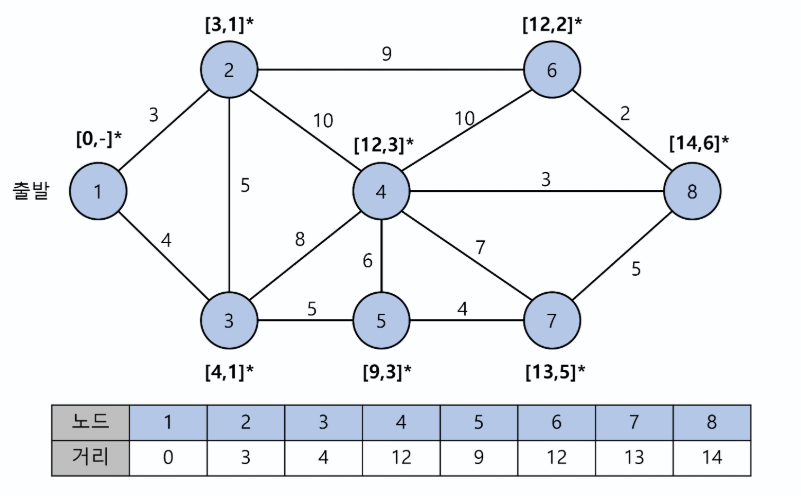
결국 1번 노드에서 다른 모든 노드로 가는 경로와 최단거리를 알 수 있고, 목적지 8번 노드까지의 거리는 14임을 알 수 있다.

최단 경로의 경우 각 노드의 부모노드를 쭉 트래킹하면 8 <- 6 <- 2 <- 1을 얻을 수 있다.
(8번 노드의 부모노드는 6번 노드)