러프하게 적어놓은거라 수정 필요!

알고리즘의 성능을 평가하는 기준으로, 시간 복잡도, 공간 복잡도

Big O 표기법과 시간 복잡도

• 빅오 표기법은 알고리즘 최악의 복잡도(상한)를 수학적으로 표현한 것
• 빅오 표기법은 알고리즘의 복잡도를 단순화하기 위해서 사용됨
• 빅오 표기법에서 중요하지 않은 상수와 같은 숫자는 모두 제거

선형 검색

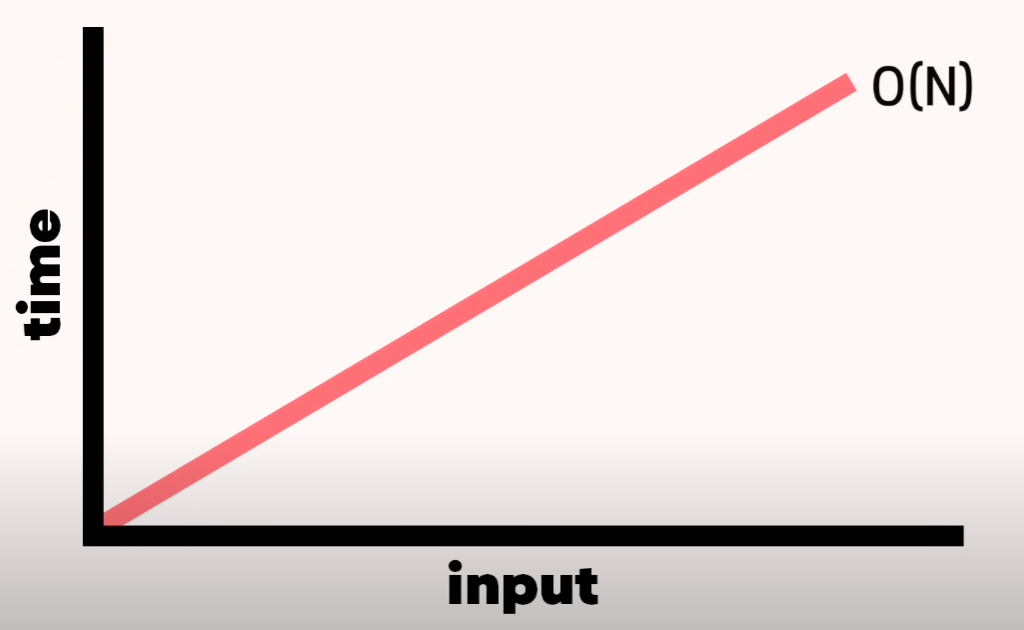
선형 검색의 시간 복잡도는 O(N)

arr1 = []

def print_first(arr):
	print(arr[0]) <- 배열의 첫번째 요소만 탐색

위 함수는 인풋이 얼마나 크던 상관없이 끝내는데 동일 숫자의 스텝이 필요
시간복잡도는 상수 시간(Constant Time)이다.

• step이 200개라도 여전히 상수시간으로 계산되기 때문에 O(1)이다.

arr = [1,2,3 ... 9,10]
def print_all(arr);
	for n in arr:
    print(n)

위 함수의 빅오 표현법은 O(N), 상수는 관계가 없다.

def print_all(arr);
	for n in arr:
    print(n)
    for n in arr:
    print(n)

위 함수를 빅오표현법을 이론적으로는 O(2N)이 맞지만 2는 상수이기 때문에 버린다.
즉 O(N)으로 표현

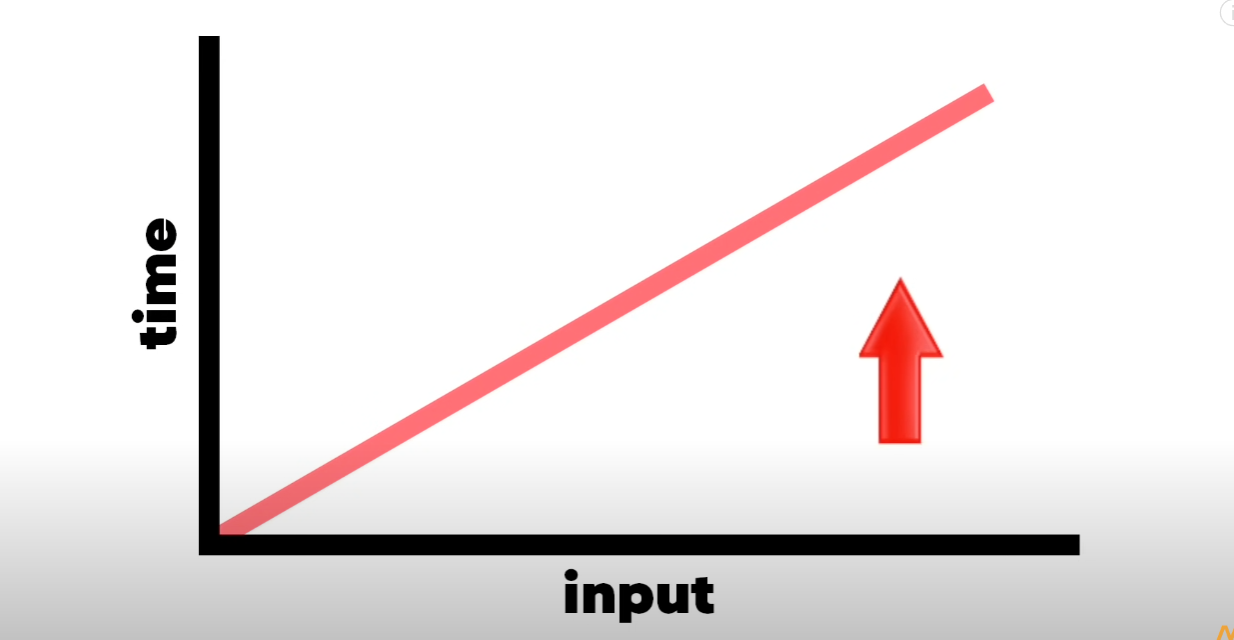
위 함수들은 input이 증가하게되면 시간도 선형적으로 늘어난다.

Quadratic Time(2차 시간)

2차 시간은 중첩 반복문이 있을 때 발생한다.

def print_twice(arr):
	for i in arr:
		for j in arr:
			print(i,n)

위 함수는 배열의 각 아이템에 대하여 루프 반복 실행
시간복잡도는 인풋의 n^2이다. (인풋이 10이라면 10^2 = 100)

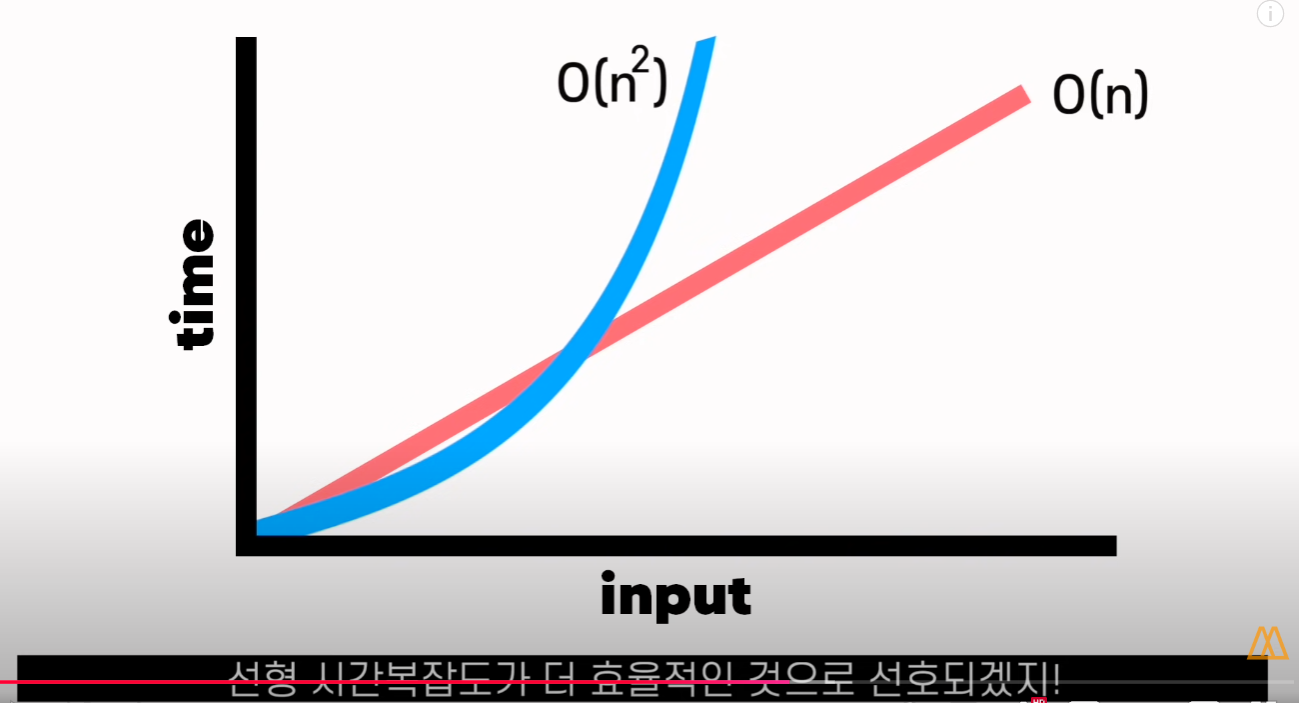
선형검색과 2차 시간이랑 비교하면 2차 시간이 더 효율적인 것으로 여겨진다.