자료구조 & 알고리즘

자료구조

• 데이터를 저장하고 관리하는 방법
• 효과적으로 저장, 검색,수정 할 수 있도록 구조화하여 데이터를 저장

주요 자료구조

1. 리스트
2. 연결 리스트
3. 스택
4. 큐
5. 트리
6. 그래프
7. 해시 테이블

1. 리스트

순서에 따라 데이터를 물리적 순서로 저장하는 자료구조

arr = [1,2,3,4,5]

print(arr[1])

연산의 복잡도 O(1)

장점과 단점

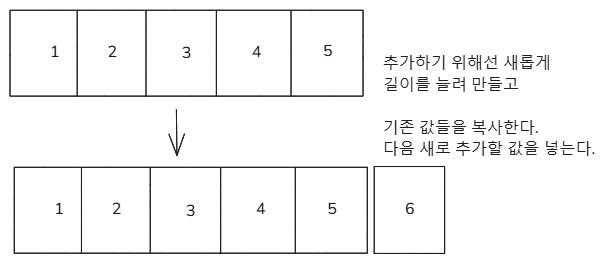
데이터의 접근성이 우수하지만 연달아 있어야 한다는 구조적 특징 때문에 데이터를 계속 추가하거나 삭제하는 등 데이터의 개수가 달라지는 연산에 취약하다.
→ 배열의 특성상 동적으로 크기를 줄이거나 추가하기 어렵다.

정해진 크기를 넘어서 데이터를 추가하기 위해선 더 이상 연달아 있는 공간이 없기 때문

2. 연결리스트

순서를 가지고 있지만 제한없이 저장할 수 있는 연결리스트
어떤 값이 다음 값을 가리키는 구조

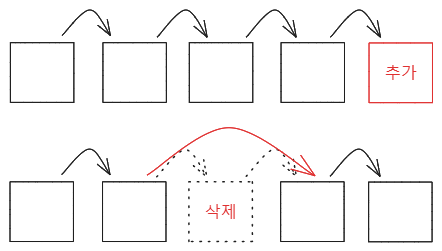
물리적인 순서가 아닌 논리적인 순서가 존재한다.
크기에 대한 제한이 없다.
추가, 삭제 등의 변경에 용이하다.

리스트의 단점을 보안했지만
연결 리스트의 단점으로는 데이터의 접근성이 기존 리스트보다 떨어진다.

내가 n번째의 데이터에 접근하기 위해선
n-1 번째의 데이터를 거치고 거쳐 n번째 데이터에 접근할 수 있게된다 (순차 접근 방식)

구현이 복잡하고 특정 항목을 탐색 혹은 추출하려 할 때 시간이 배열로 구현한 순차 리스트 보다 오래 걸린다는 단점

추가 리스트 자료구조들

1. 원형 연결 리스트
2. 이중 연결 리스트
   참고 : https://taco99.tistory.com/7

3. 스택

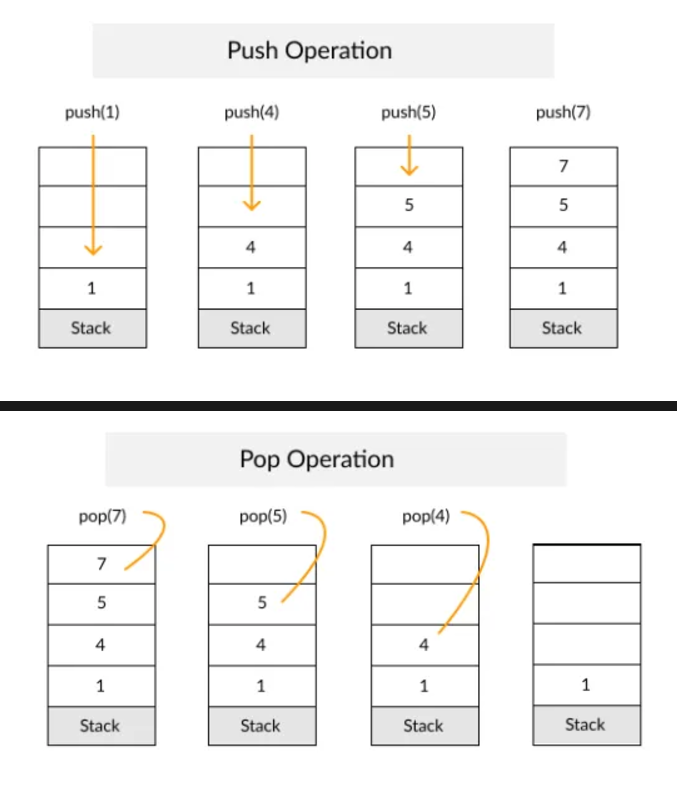
IN : 1 → 2 → 3
OUT : 3 → 2 → 1

1번 2번 3번 이 순서대로 들어 갔지만 나올 땐 역순으로 됨 (후입선출)
LIFO : Last In First Out

4. 큐(Queue)

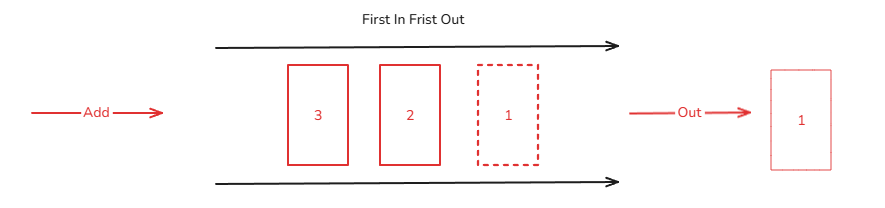
한쪽에선 입력만 한쪽에선 출력만 발생하기 때문에
먼저 들어온 데이터가 먼저 나간다.
Ex) 티켓팅 예메, 뱅킹 시스템과 같은 번호표의 체계가 큐다

class Stack:
    def __init__(self):
        self.stack = []

    def push(self, item):
        self.stack.append(item)

    def pop(self):
        if not self.is_empty():
            return self.stack.pop()
        else:
            raise IndexError("pop from empty stack")

    def peek(self):
        if not self.is_empty():
            return self.stack[-1]
        else:
            raise IndexError("peek from empty stack")

    def is_empty(self):
        return len(self.stack) == 0

    def __str__(self):
        return str(self.stack)

5. 그래프

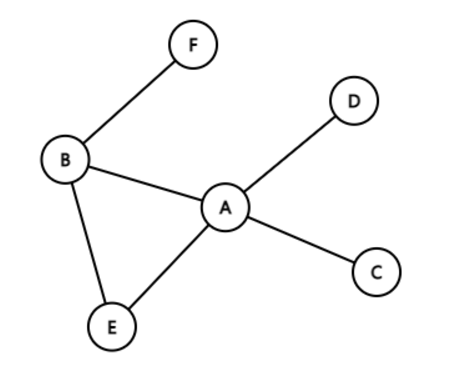
원소간의 관계를 표현한 자료구조

참고 : https://leejinseop.tistory.com/43

6. 트리

계층 구조를 나타내는 구조

값을 정렬하거나, 순서에 맞게 구조화해서 저장하는데 유용
검색(탐색)의 이점이 크다.

BE에서는 이진트리, 빅트리 등을 사용한다.

해시 테이블

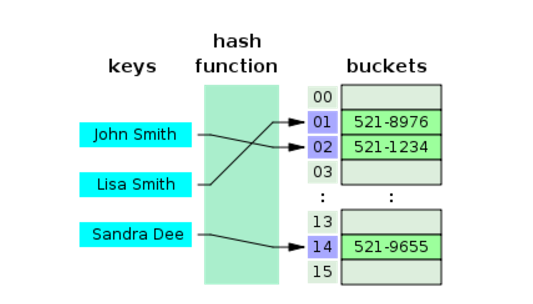
(Key, Value)로 데이터를 저장하는 자료구조
해시 테이블이 빠른 검색속도 제공하는 이유?
→ 내부적으로 배열(버킷)을 사용하여 데이터를 저장한다.

해시테이블은 각각의 key에 해시함수를 적용해 배열의 고유한 인덱스를 생성하고, 이 인덱스 값을 활요해 값을 저장하거나 검색하게 된다. 여기서 실제 값이 저장되는 장소를 버킷 또는 슬롯이라고 한다.

( 비트코인 지갑 생성원리를 생각하면 될 듯)

---

알고리즘

문제를 해결하기 위한 단계적 절차와 방식을 의미

주요 알고리즘

1. 정렬 알고리즘

데이터를 특정 순서대로 정렬하는 알고리즘
Ex_) 버블 정렬, 퀵 정렬, 병합 정렬

2. 탐색 알고리즘

데이터에서 특정 값을 찾는 알고리즘
Ex_) 이진 탐색, 선형 탐색

3. 그래프 알고리즘

그래프 자료구조를 탐색하거나, 최단 경로를 찾는 알고리즘
Ex_) Breadth First Search(너비 우선 탐색), Depth First Search(깊이 우선 탐색)

4. 동적 계획법

복잡한 문제를 작은 부분 문제로 나누어 푸는 알고리즘
Ex_) 피보나치 수열

5. 그리디 알고리즘

현재 상황에서 가장 좋은 선택을 하는 알고리즘
Ex_) 최소 신장 트리