트리

• 그래프의 특별한 형태

• 사이클이 없으며 모든정점이 연결된 무방향 그래프

• 구성 요소

  • 루트 노드 : 계층 구조의 시작 노드
  • 부모 자식 관계 : 트리의 모든 노드 간의 관계는 부모-자식 관계를 나타냄
  • 리프 노드 : 자식 노드를 갖지 않는 노드
  • 서브 트리 : 특정 노드와 그 자손 노드로 구성된 부분 그래프

• 트리의 종류

  • 이진 트리 : 최대 두 개의 자식 노드를 가지는 트리
  • 이진 탐색 트리 : 이진 트리에 값의 순서가 부여된 트리
    • 왼쪽 자식 노드 : 부모의 값보다 작은 값
    • 오른쪽 자식 노드 : 부모의 값보다 큰 값
  • 균형 트리(Balanced Tree): 트리의 리프노드가 같은 레벨이 있도록 구성된 트리
  • 힙 : 특정한 조건을 만족하는 이진 트리

• 트리의 표현

  • 인접 행렬
  • 인접 리스트
  • 배열
    • 배열을 사용해 이진 트리를 표현할 수 있다.
    • 루트 노드의 배열의 첫 번째 요소에 저장
    • 노드 i의 왼쪽 자식은 배열의 (2i + 1) 번째 요소
    • 노드 i의 오른쪽 자식은 배열의 (2i + 2) 번째 요소

  class BinaryTree:
     def __init__(self, size):
         self.size = size
         self.tree = [None] * size
  
     # 루트 노드 값 설정
     def set_root(self, value):
         self.tree[0] = value
  
     # 왼쪽 자식 값 설정
     def set_left(self, parent_index, value):
         left_index = 2 * parent_index + 1
         if left_index < self.size:
             self.tree[left_index] = value
         else:
             print("Index out of bounds for left child")
  
     # 오른쪽 자식 값 설정
     def set_right(self, parent_index, value):
         right_index = 2 * parent_index + 2
         if right_index < self.size:
             self.tree[right_index] = value
         else:
             print("Index out of bounds for right child")
  
      # 트리 인스턴스 생성
     bt = BinaryTree(7)
     bt.set_root(1)
     bt.set_left(0, 2)
     bt.set_right(0, 3)
     bt.set_left(1, 4)
     bt.set_right(1, 5)
     bt.set_left(2, 6)
     bt.set_right(2, 7)

이진 트리 순회

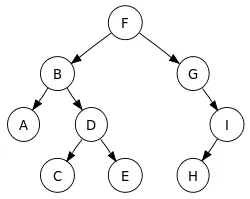
• 트리의 모든 노드를 방문하는 기본적인 방식

1. 전위 순회 (Pre-order Traversal)
   • 현재 노드 → 왼쪽 서브 트리 → 오른쪽 서브트리
2. 중위 순회 (In-order Traversal)
   • 왼쪽 서브트리 → 현재 노드 → 오른쪽 서브트리
3. 후위 순회 (Post-order Traversal)
   • 왼쪽 서브트리 → 오른쪽 서브트리 → 현재 노드

최소 신장 트리 (MST)

• 그래프의 모든 정점을 포함하며, 사이클이 없는 연결된 그래프
• 최소 신장 트리 (Minimum spanning Tree) 는 신장트리 중 간선의 가중치 합이 가장 작은 트리
  

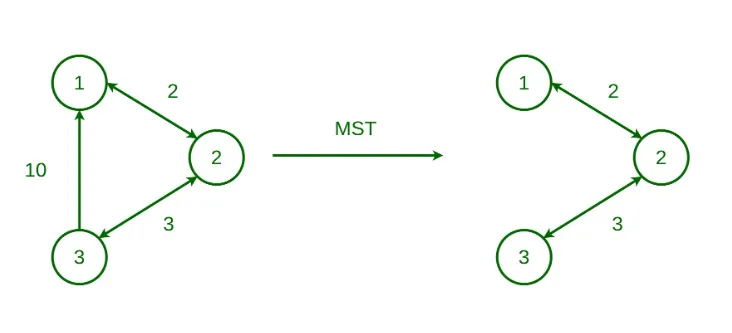
크루스칼 알고리즘

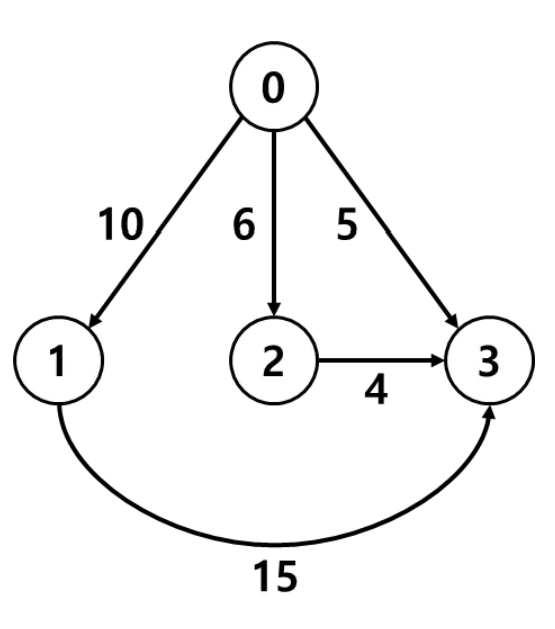
• 간선 중심의 접근 방법

• 그래프의 모든 간선의 집합 $E$를 만든다.

• $E$가 비어있지 않을 때까지
  1. $E$의 간선들 중 가중치가 최소인 간선을 지운다.
  2. 삭제된 간선이 가리키는 정점 $(x,y)$를 연결해도 사이클이 발생하지 않으면 연결

  class Edge:
     def __init__(self, src, dest, weight):
         self.src = src
         self.dest = dest
         self.weight = weight
  
     def __lt__(self, other):
         return self.weight < other.weight
  
  		class Kruskal:
     def __init__(self, vertices, edges):
         self.V = vertices
         self.E = edges
         self.edges = []
  
     def find(self, parent, i):
         if parent[i] == -1:
             return i
         return self.find(parent, parent[i])
  
     def union(self, parent, x, y):
         xset = self.find(parent, x)
         yset = self.find(parent, y)
         if xset != yset:
             parent[xset] = yset
  
     def mst(self):
         self.edges.sort()
         parent = [-1] * self.V
         mst = []
  
         for edge in self.edges:
             x = self.find(parent, edge.src)
             y = self.find(parent, edge.dest)
  
             if x != y:
                 mst.append(edge)
                 self.union(parent, x, y)
  
         print("Following are the edges in the constructed MST")
         for edge in mst:
             print(f"{edge.src} -- {edge.dest} == {edge.weight}")
  
  		def main():
     V = 4
     E = 5
     graph = Kruskal(V, E)
  
     graph.edges.append(Edge(0, 1, 10))
     graph.edges.append(Edge(0, 2, 6))
     graph.edges.append(Edge(0, 3, 5))
     graph.edges.append(Edge(1, 3, 15))
     graph.edges.append(Edge(2, 3, 4))
  
     graph.mst()
  
  		if __name__ == "__main__":
     main()

프림 알고리즘

• 정점 중심의 접근 방법
• 임의의 시작 정점을 선택한다
• 현재의 트리에서 연결된 간선 중 최소 가중치 간선의 정점을 선택하여 트리에 추가
• 새로 연결된 정점에서 다시 최소 가중치 간선의 정점을 선택하여 추가
• 모든 정점이 연결될 때까지 과정 반복

import sys

class Prim:
    def __init__(self, vertices):
        self.V = vertices

    def min_key(self, key, mst_set):
        min = sys.maxsize
        min_index = -1

        for v in range(self.V):
            if not mst_set[v] and key[v] < min:
                min = key[v]
                min_index = v

        return min_index

    def print_mst(self, parent, graph):
        print("Edge \tWeight")
        for i in range(1, self.V):
            print(f"{parent[i]} - {i} \t{graph[i][parent[i]]}")

    def mst(self, graph):
        key = [sys.maxsize] * self.V
        parent = [None] * self.V
        mst_set = [False] * self.V

        key[0] = 0
        parent[0] = -1

        for _ in range(self.V - 1):
            u = self.min_key(key, mst_set)
            mst_set[u] = True

            for v in range(self.V):
                if graph[u][v] and not mst_set[v] and key[v] > graph[u][v]:
                    key[v] = graph[u][v]
                    parent[v] = u

        self.print_mst(parent, graph)

def main():
    graph = [
        [0, 2, 0, 6, 0],
        [2, 0, 3, 8, 5],
        [0, 3, 0, 0, 7],
        [6, 8, 0, 0, 9],
        [0, 5, 7, 9, 0]
    ]

    prim = Prim(len(graph))
    prim.mst(graph)

if __name__ == "__main__":
    main()