1. 그래프

그래프는 정점과 간선으로 이루어진 자료구조 G = (V, E)

• 정점(vertex) 간선(edge) 으로 구성된 자료구조
• 정점은 데이터를 나타내고, 간선은 데이터 간의 관계를 의미한다.
• 구성요소
  • 간선(Edge) : 정점 간의 관계를 나타내며, 방향성이 있을 수도 있다.
  • 정점(Vertex) : 데이터 자체를 의미한다.
• 그래프의 종류
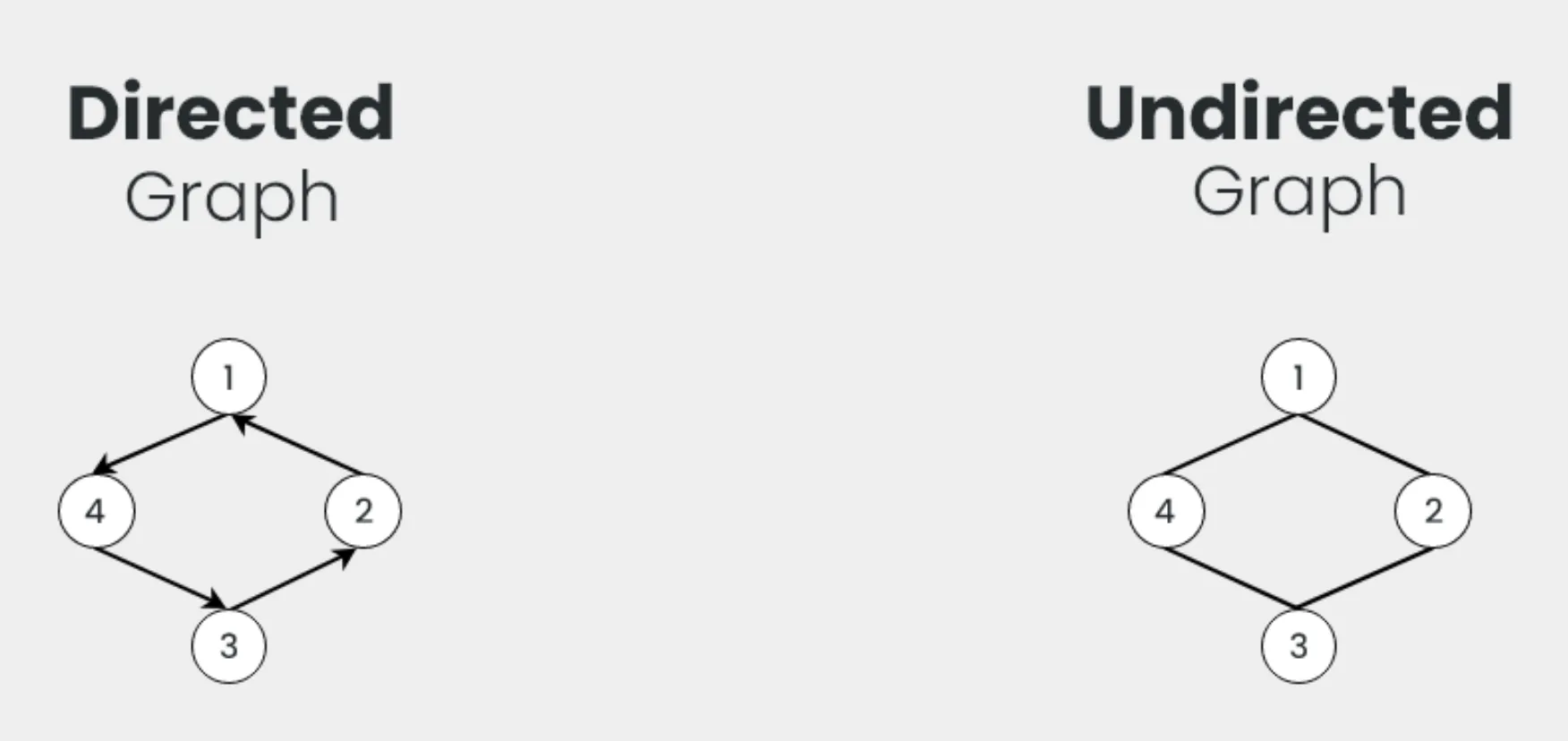
  • 방향 그래프(Directed Graph) : 간선에 방향이 있는 그래프
  • 무방향 그래프(Undirected Graph) : 간선에 방향이 없는 그래프
  • 가중치 그래프(Weighted Graph) : 간선에 가중치(수치) 가 있는 그래프
    

그래프의 표현

• 인접 행렬

  • 2차원 배열을 사용해 그래프의 정점들 간의 연결 관계를 0,1을 통해 표현
  • 행렬의 (i,j) 위치에 간선의 유무를 나타내며,
  • 무방향 그래프의 경우 간선이 존재하면 1, 없으면 0
  • 방향 그래프는 i에서j방향의 간선이 존재하면 1, 없으면 0 표현
  • 가중치 그래프는 간선이 존재하면 간선의 가중치, 없으면 0 표현

• 장점

  • 단순한 구조로 구현이 쉬움
  • $O(1)$ 시간 복잡도로 간선의 존재 확인 가능

• 단점

  • $O(N^2)$의 높은 공간 복잡도를 필요

    class GraphAdjMatrix:
    def __init__(self, vertices):
        self.vertices = vertices
        self.adj_matrix = [[0] * vertices for _ in range(vertices)]
  
    def add_edge(self, src, dest):
        self.adj_matrix[src][dest] = 1
        self.adj_matrix[dest][src] = 1
  
    def remove_edge(self, src, dest):
        self.adj_matrix[src][dest] = 0
        self.adj_matrix[dest][src] = 0
  
    def is_edge(self, src, dest):
        return self.adj_matrix[src][dest] != 0

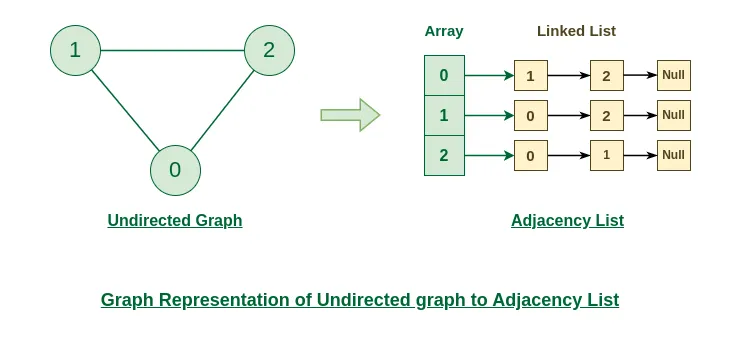
인접 리스트

• 정점에 연결된 다른 정점들의 리스트로 그래프 표현
• 인접 리스트(Adjacency List)
  • 각 정점에 대해 연결된 정점들의 목록을 저장
  • 각 정점은 리스트를 저장
  • 정점과 연결된 다른 정점들의 참조를 포함
• 장점
  • 공간 효율성이 좋음
  • 특정 정점의 인접 정점을 빠르게 찾을 수 있다.
• 단점
  • 두 정점 간의 간선 존재를 확인을 위해 $O(V)$ 의 시간 복잡도.
    

class GraphAdjList:
    def __init__(self, vertices):
        self.vertices = vertices
        self.adj_list = [[] for _ in range(vertices)]

    def add_edge(self, src, dest):
        self.adj_list[src].append(dest)
        self.adj_list[dest].append(src)

    def remove_edge(self, src, dest):
        self.adj_list[src].remove(dest)
        self.adj_list[dest].remove(dest)

    def is_edge(self, src, dest):
        return dest in self.adj_list[src]