정렬 알고리즘
- 정렬 알고리즘은 데이터를 기준에 맞추어 순서대로 나열하는 것을 목표로 함
- 데이터를 구조화하여, 탐색, 분석 등의 작업을 효과적으로 수행 가능
- 알고리즘의 동작방식과 성능을 이해하고 활용할 수 있음
알고리즘 종류
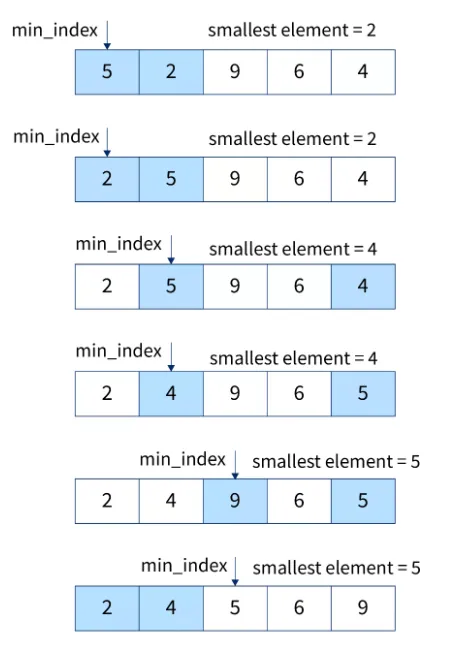
1. 선택 정렬
- 정렬 대상의 데이터 중 가장 작은 데이터를선택해 앞으로 위치시키는 정렬 방법
쉽게 오름차순
- O(N2)의 복잡도를 갖는다.
- 매번 작은 데이터를 찾는 과정 중 불필요하게 중복되는 연산이 있지만 구현이 간단함
def selection_sort(arr):
for i in range(len(arr)):
min_idx = i
for j in range(i+1, len(arr)):
if arr[j] < arr[min_idx]:
min_idx = j
arr[i], arr[min_idx] = arr[min_idx], arr[i]
return arr
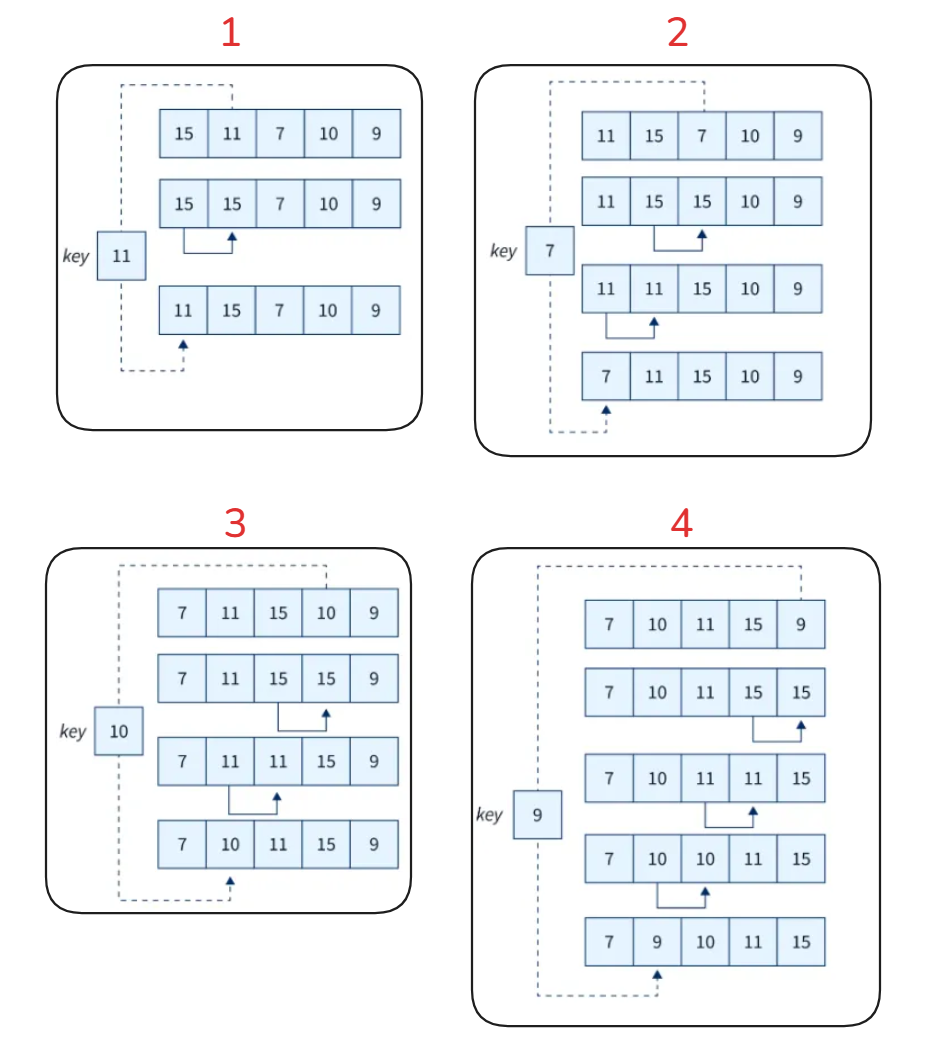
2. 삽입 정렬
- 데이터를 순차적으로 정렬 순서에 맞추어 삽입하는 정렬 방법
- 어느 정도 정렬된 데이터의 경우 정렬 시간이 빠르다.
- 최악의 경우 O(N2), 최상의 경우 O(N)의 시간 복잡도를 갖는다.
def insertion_sort(arr):
for i in range(1, len(arr)):
key = arr[i]
j = i - 1
while j >= 0 and key < arr[j]:
arr[j + 1] = arr[j]
j -= 1
arr[j + 1] = key
return arr
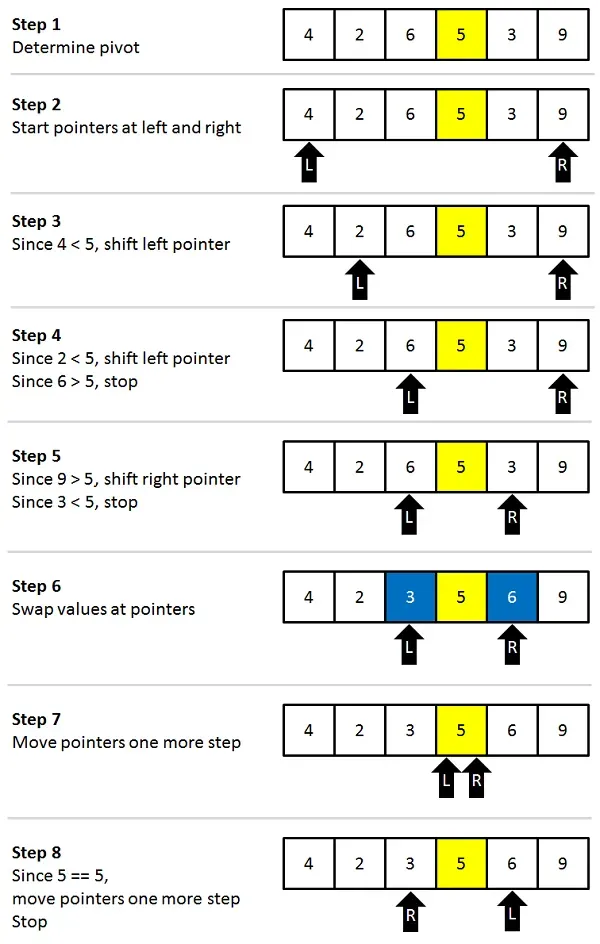
3. 퀵 정렬
- 피봇(기준이 되는 수)에 의해 분할과 정렬 후 합치는 과정 반복(재귀)
- 기준을 설정한 후 큰 수와 작은 수를 교환하고 리스트를 반으로 나눈다.
- 대표적인 분할 방식으로는 리스트에서 첫 번째 데이터를 피봇으로 정하는 호어 분할 방식
- 퀵 정렬의 평균 시간 복잡도 O(NlogN)
def quick_sort(arr):
if len(arr) <= 1:
return arr
pivot = arr[len(arr) // 2]
left = [x for x in arr if x < pivot]
middle = [x for x in arr if x == pivot]
right = [x for x in arr if x > pivot]
return quick_sort(left) + middle + quick_sort(right)
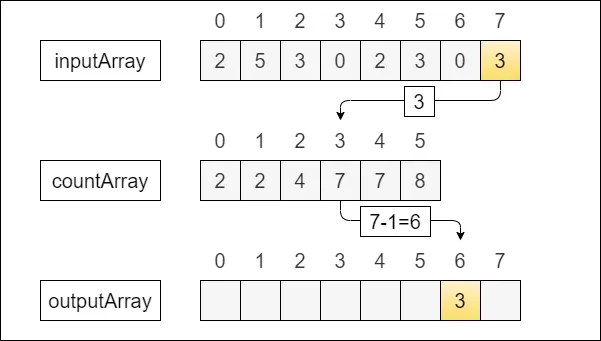
4. 계수 정렬
- 비교 기반의 정렬 알고리즘이 아닌 정수를 정렬하는 특정 상황에서 매우 효율적
- 제한된 수의 정수들을 정렬할 때 유용하게 사용된다. (1≤K≤100)
- 시간복잡도 O(n+k)
- 별도의 카운트 배열을 유지하기 때문에 정렬 데이터의 범위가 크면 메모리 낭비가 발생
- 계수 정렬은 특정 상황에서 더 빠를 수 있으며 데이터의 범위에 따라 성능이 결정된다.
def counting_sort(arr):
if not arr:
return arr
max_val = max(arr)
count = [0] * (max_val + 1)
for num in arr:
count[num] += 1
result = []
for i, c in enumerate(count):
result.extend([i] * c)
return result




