선형대수학

화살표 같은 것 -> 크기와 방향이 존재한다.\*벡터의 기하학적 특성을 반영 -> 특히 좌표계의 변환에 대해 불변한다.뭔소리지? 이해가 안된다. -> 축이 바뀌더라도 벡터 그 자체는 가만히 있는다.위의 그림처럼 축이 바뀌더라도 벡터는 바뀌지 않는다. 다만 벡터의 성분이

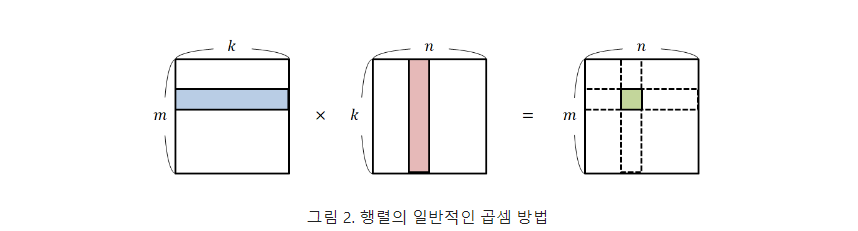
이를 수식으로 정확히 쓰자면왼쪽 행렬에서는 행을, 우측 행렬에서는 열을 가져와 계산하는 것을 알 수 있다.가져온 행 또는 열을 벡터로 생각한다면 계산된 행열의 각 원소 값은 벡터의 내적을 표현한 것으로 볼 수 있다.이를 통해 일반적인 행렬의 곱은 행벡터와 열벡터의 내적

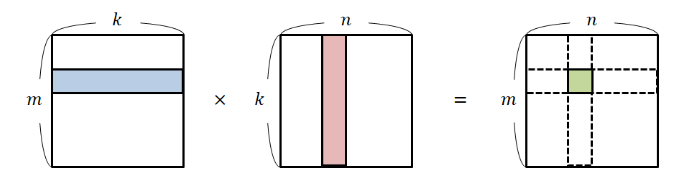
지금까지 벡터가 무엇인지에 대해 알아보고, 행렬과 벡터의 곱에 대해서 공부했다.벡터란 상수배(곱셈 규칙)와 덧셈 규칙이 정의되는 원소들이고, 이들의 집합에 이 연산들이 정의된 집합을 벡터 공간이라고 했다.여기서 상수배와 덧셈 규칙이 정의되는 원소들은 '선형성을 가진다'