일반적인 행렬 곱의 형태
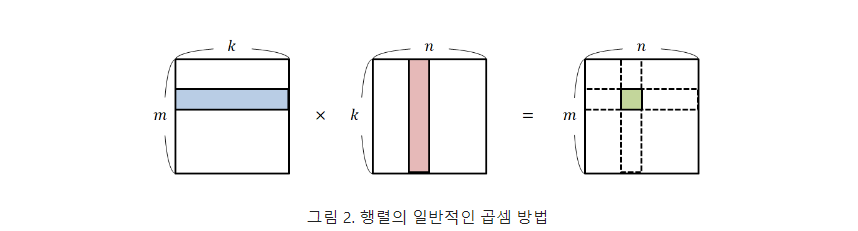
이를 수식으로 정확히 쓰자면
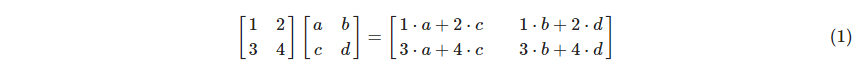
왼쪽 행렬에서는 행을, 우측 행렬에서는 열을 가져와 계산하는 것을 알 수 있다.
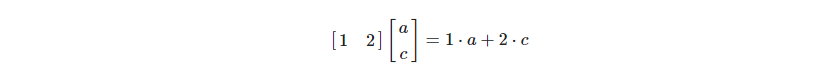
가져온 행 또는 열을 벡터로 생각한다면 계산된 행열의 각 원소 값은 벡터의 내적을 표현한 것으로 볼 수 있다.
이를 통해 일반적인 행렬의 곱은 행벡터와 열벡터의 내적을 계산함으로써 행렬 곱이 이루어 진다는 것을 알 수 있다.
주목해야할 점은 행벡터와 열벡터 간의 연산이 이루어 진다는 점이다.
- 다음시간에 배워보자
이러한 관점을 응용한 개념으로는 공분산 행렬이 있다.
열벡터의 선형결합
이번에는 행렬과 벡터의 곱을 생각해보자.
위의 행렬 식에서 b, d를 제거한 벡터를 곱해보자
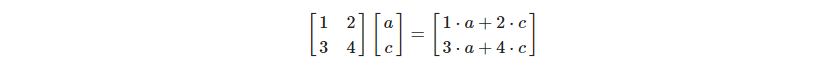
이 식을 바꿔서 쓰면 이런 식으로 나오게 된다.
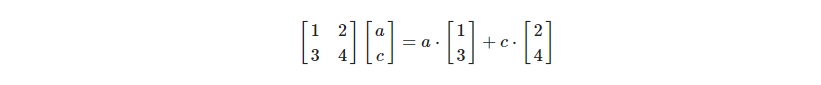
벡터의 선형결합과 동일한 형태의 식으로 만들 수 있다.
이처럼 행렬과 벡터의 곱은 행렬을 구성하는 두 열벡터의 선형결합을 다른 방식으로 표현한 것으로 볼 수 있다.
열공간을 기반한 해석
벡터의 선형결합이 의미하는 것은 벡터공간의 생성이다.
위에서 행렬과 벡터의 곱을 두 열벡터의 선형결합으로 볼 수 있다고 했다. -> 벡터 공간이 생기겠네?
그래서 이 행렬과 벡터의 곱이 우리에게 묻는 것은 "주어진 열벡터를 이용해 만들 수 있는 벡터공간(열공간)에 대한 탐구"라는 점에서 중요하다.
이런 관점에서 아래 수식의 의미를 생각해보자
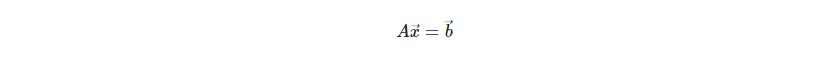
행렬 A와 x벡터를 곱한 것이 b벡터가 되는 것이다.
그럼 이 식이 성립한다면 벡터공간이 형성되는 것이겠지? -> 그럼 셋 중 두 개만 알아도 나머지를 알 수 있을 것이다?
나는 그렇게 이해했다.
예를 들며 이해해보자
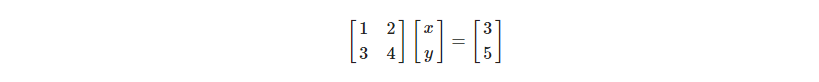
이 문제에서 x, y를 알고 싶으면 연립방정식으로 해결할 수 있다.
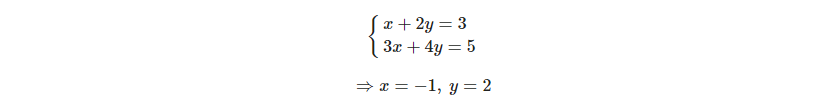
하지만 이 식을 각 열벡터의 선형결합으로 생각해보자
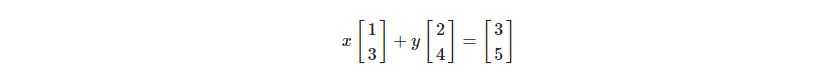
그럼 이 식을 열공간을 기반한 해석으로 해석해보자.
이 두 벡터로부터 생성된 공간 안에 (3,5)가 존재하는가?
존재한다면 그 때의 x,y의 의 조합이 어떻게 되는가?
이정도 인 것 같다.
이러한 관점에서 선형대수를 응용하면 선형연립방정식, 선형회귀등을 할 수 있다.
선형 변환을 기반한 해석
이 친구는 이해하는데 많은 노력이 필요했다. 도대체 무슨 소리일까..... 하며 10분을 앉아있다가 그림을 그리며 이해를 했다.
행렬과 벡터의 곱이 열벡터의 선형결합이라는 해석이 우리에게 주는 또 다른 관점은 행렬과 벡터의 곱을 기저 벡터의 변형을 통한 벡터의 선형변환으로 해석할 수 있도록 도움을 주기 때문이다.
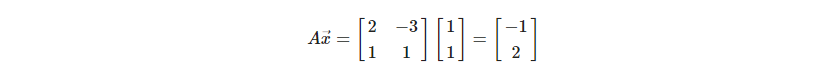
이 문장과 예시인 이 식을 내가 이해한 단계대로 해체해보겠다.
기저벡터는 뭐지?? -> n차원 공간에서 임의의 벡터를 표현할 수 있는 기준이 되는 벡터 -> 2차원에서는 2개의 벡터가 있어야 기저벡터가 이루어짐 또한 벡터가 서로 선형독립적이거나 행렬식이 0이 되지 않아야함
-> 먼소리지?
결과값이 0인 열벡터에 대해 각 벡터에 상수배(k배)를 했을 때 이 k가 모두 0인 벡터가 선형독립적인 벡터이다.
이걸 보면 이해가 좀 된다.
이제 해체해보겠다.
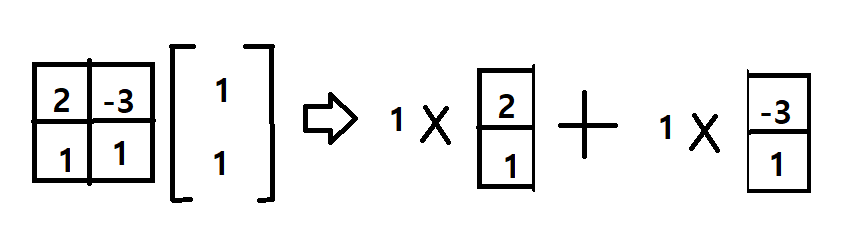
이렇게 되면 (2,1) , (-3, 1)인 공간에서 (1, 1)만 진행한 벡터라고 이해할 수 있다. -> 먼 개소리지?
사진을 보면 이해가 된다.
전(before)
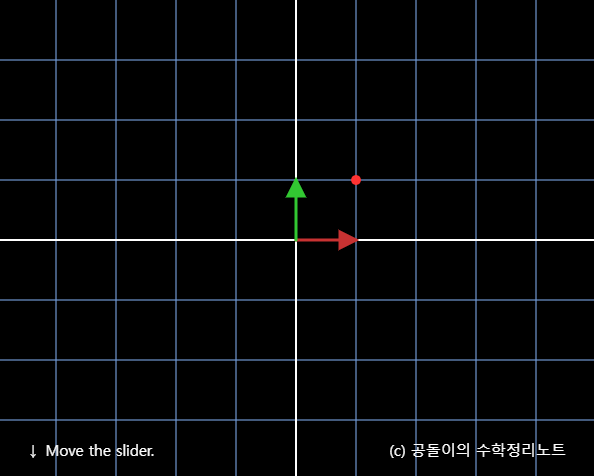
후(after)
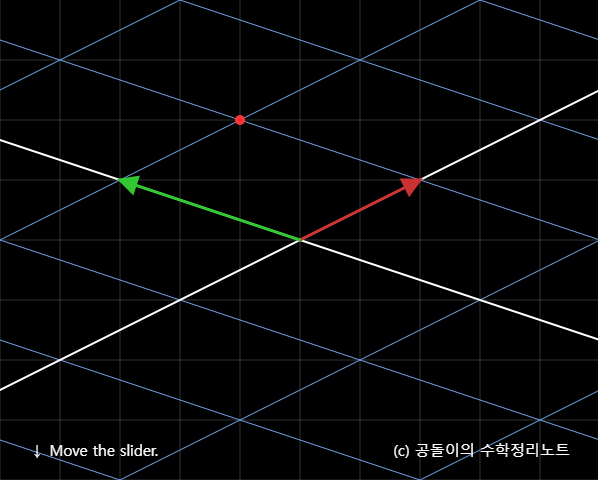
후 사진에서 원래의 좌표계를 보게되면 축이 (2,1) (-3,1)인 것을 볼 수 있다. 거기서 (1, 1)만큼 진행한 벡터라고 볼 수 있는 것이다.
-> 새로운 두 기저벡터의 1배와 1배의 합으로 나타낼 수 있다는 뜻이다.
다음에 행렬과 선형변환을 공부할 것이니 여기까지만 하겠다.
이러한 관점을 이용한 선형대수학의 응용은 고윳값과 고유벡터, 주성분 분석(PCA), 특이값 분해(SVD) 등이 있다.
Ref : https://angeloyeo.github.io/2020/09/08/matrix_multiplication.html
유튜브 강의도 정말 잘해주신다.
공돌이의 수학노트 최고
