정렬 알고리즘
정렬 알고리즘(sorting algorithm)은 원소들을 일정한 순서대로 열거하는 알고리즘이다.
정렬 알고리즘을 소리로 표현한 영상
정렬 알고리즘 애니메이션
O(n²) 정렬
버블 정렬(Bubble Sort)
이렇게 이름지어진 이유는 정렬하는 모습이 거품이 꺼지는 모습과 비슷하기 때문이라고 한다.
 이미지 출처
이미지 출처 y축: 값의 크기 x축: 값의 인덱스
개념 (오름차순 정렬 기준)
버블 정렬은 매번 연속된 두개 인덱스를 비교한다.
비교시마다 큰 값이 뒤로 교체되고 다음 인덱스로 이동 후 비교한다.
한 바퀴 돌 때마다 가장 마지막에는 비교하는 수들 중 가장 큰 값이 저장되므로
다음 바퀴를 돌 때에는 가장 마지막 수는 제외하고 진행한다.
예제 (오름차순 정렬 기준)
- 수열의 왼쪽 끝에 있는 두 숫자를 비교한다.
- 첫 번째 순회 (First Pass)
e.g.) 6과 3을 비교- 비교한 결과 오른쪽 숫자가 작으면 왼쪽과 바꾼다.
e.g.) 6 > 3 이므로 좌우의 숫자를 교환- 교체 후 한 칸 오른쪽으로 이동한다.
- 동일한 방법으로 숫자를 비교한다.
e.g) 6과 0: 6 > 0 이므로 교환- 동일한 작업을 오른쪽 끝의 숫자에 이동하기 까지 반복한다.
e.g) 6과 5: 6 > 5 이므로 교환
6과 1: 6 > 1 이므로 교환- 오른쪽 끝에 도착하면 수열 중에서 가장 큰 숫자가 오른쪽 끝으로 이동했다.
- 오른쪽 끝 숫자는 정렬을 끝낸 것으로 간주한다.
e.g) 6은 정렬 완료- 다시 왼쪽 끝에서 부터 시작한다.
- 동일한 작업을 모든 숫자가 정렬될 때까지 반복한다.
- 두 번째 순회 (Second Pass)
e.g.) 3과 0: 3 > 0 이므로 교환
3과 5: 3 < 5 이므로 그대로
5와 1: 5 > 1 이므로 교환
-세 번째 순회 (Third Pass)
0과 3: 0 < 3 이므로 그대로
3과 1: 3 > 1 이므로 교환
-네 번째 순회 (Fourth Pass)
0과 1: 0 < 1 이므로 그대로
정렬 완료
단점
- 가장 왼쪽에 있는 하나의 값이 가장 오른쪽으로 이동하기 위해서는 배열의 모든 다른 요소들과 교체되어야 한다.
- 일반적으로 자료의 교환(swap) 작업이 자료의 이동(move) 작업보다 더 복잡하기 때문에 거의 쓰이지 않는다.
시간복잡도
- 최선의 경우: 자료가 이미 정렬되어 있는 경우 -
O(n²)
- 비교 횟수:
n-1, n-2, … , 2, 1 번 = n(n-1)/2 - 교환 횟수: 일어나지 않음
- 최악의 경우 : 자료가 역순으로 정렬되어 있는 경우 -
O(n²)
- 비교 횟수 :
n(n-1)/2 번 - 교환 횟수 :
n(n-1)/2 번
평균 및 최악 실행 시간: O(n²)
메모리(공간 복잡도): O(1)
선택 정렬(Selection Sort)
버블 정렬과 비슷하지만 보다 개선된 정렬이다.
버블 정렬보다 보통 2배 정도 빠르다.
개념 (오름차순 정렬 기준)
수열을 선형 탐색해서 최솟값을 찾는다.
최솟값을 열의 왼쪽 끝에 있는 값과 교환하고 정렬을 완료한다.
(최솟값이 이미 왼쪽 끝에 있으면 아무런 작업도 하지 않는다)
동일한 작업을 모든 값이 정렬을 마칠 때까지 반복한다.
예제 (오름차순 정렬 기준)
- 수열을 선형 탐색해 최솟값을 찾는다.
e.g.) 1- 최솟값을 열의 왼쪽 끝에 있는 값과 교환하고 정렬을 완료한다.
e.g.) 6과 교환- 동일한 작업을 모든 값이 정렬을 마칠 때까지 반복한다.
e.g.)2: 8과 교환
3: 그대로
4: 5와 교환
5: 9와 교환
6: 10과 교환
7, 8, 9, 10: 그대로
단점
성능이 좋지 않으나 작은 수(보통 30 이하의 수)에서는 효율적이다.
시간복잡도
최악, 최선, 평균 항상 n(n-1) / 2번의 비교 연산을 수행하게 되므로 O(n²)이다.
T(n) = (n-1) + (n-2) + … + 2 + 1 = O(n²)
평균 및 최악 실행 시간: O(n²)
메모리(공간 복잡도): O(1)
삽입 정렬(Insertion Sort)
버블 정렬과 비슷하지만 보다 개선된 정렬이다.
이미 정렬되어 있는 자료구조에 자료를 하나씩 삽입하는 경우, 오버헤드가 적기 때문에 최선의 알고리즘이 된다.
개념 (오름차순 정렬 기준)
가장 앞쪽에 있는 원소는 이미 정렬이 됐다고 가정한다.
아직 작업하지 않은 원소를 이미 정렬 완료된 앞의 원소보단 크고, 뒤에 원소보단 작은 위치에 삽입하는 방법이다.
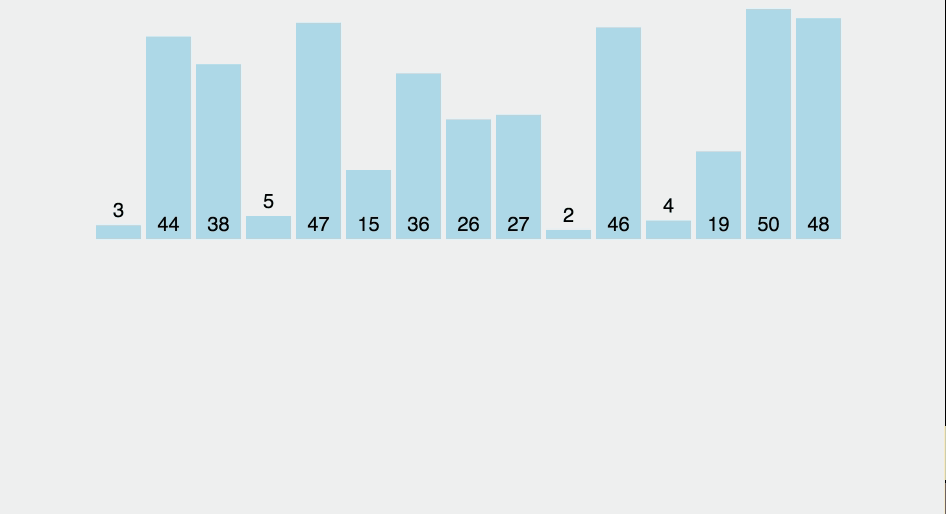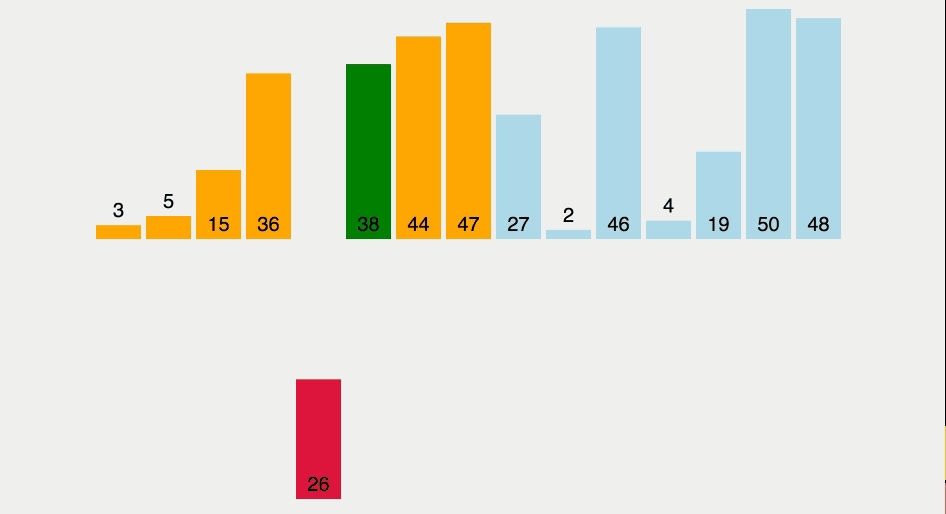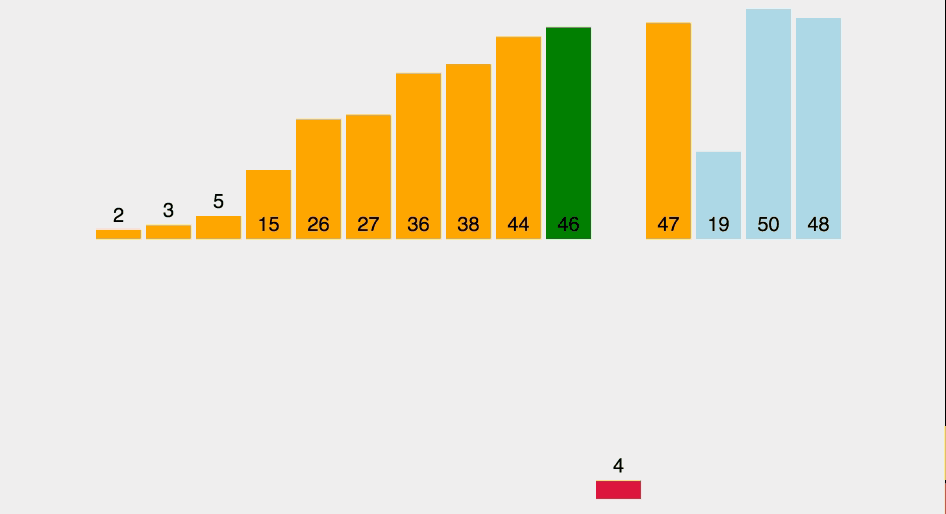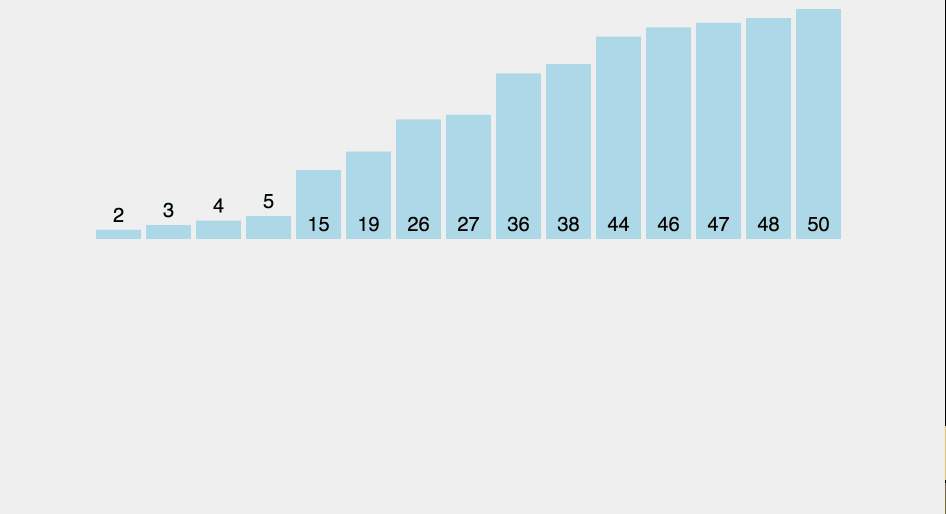
예제 (오름차순 정렬 기준)
- 가장 앞쪽에 있는 원소는 이미 정렬이 됐다고 가정한다.
e.g.) 정렬 완료:3- 아직 작업하지 않은 원소 중 하나를 이미 정렬된 원소와 비교한다.
e.g.) 3과 44: 3 < 44 이므로 3 뒤에 삽입- 정렬 완료된 상태로 변경한다.
e.g.) 정렬 완료:3 44- 동일한 작업을 모든 원소가 정렬이 완료될 때까지 반복한다.
e.g.) 38과 44: 38 < 44 이므로 옆으로 이동
38과 3: 3 < 38 이므로 3 뒤에 삽입
정렬 완료:3 38 44
5와 44: 5 < 44 이므로 옆으로 이동
5와 38: 5 < 38 이므로 옆으로 이동
5와 3: 3 < 5 이므로 3 뒤에 삽입
정렬 완료:3 5 38 44
47과 44: 44 < 47 이므로 44 뒤에 삽입
정렬완료:3 5 38 44 47
계속해서 앞의 원소보다 크고 뒤에 원소보다 작은 위치에 삽입한다
15는 5 뒤, 38 앞에 삽입
정렬 완료:3 5 15 38 44 47
36은 15 뒤, 38 앞에 삽입
정렬 완료:3 5 15 36 38 44 47
26은 15 뒤, 36 앞에 삽입
정렬 완료:3 5 15 26 36 38 44 47
27은 26 뒤, 36 앞에 삽입
정렬 완료:3 5 15 26 27 36 38 44 47
2는 3 앞에 삽입
정렬 완료:2 3 5 15 26 27 36 38 44 47
46은 44 뒤, 47 앞에 삽입
정렬 완료:2 3 5 15 26 27 36 38 44 46 47
4는 3뒤, 5 앞에 삽입
정렬 완료:2 3 4 5 15 26 27 36 38 44 46 47
19는 15뒤, 26 앞에 삽입
정렬 완료:2 3 4 5 15 19 26 27 36 38 44 46 47
50는 47뒤에 삽입
정렬 완료:2 3 4 5 15 19 26 27 36 38 44 46 47 50
48은 47뒤 50 앞에삽입
정렬 완료:2 3 4 5 15 19 26 27 36 38 44 46 47 48 50
단점
배열의 크기가 커질수록 효율이 떨어진다
시간복잡도
최선의 경우 : 자료가 이미 정렬되어 있는 경우 - O(n)
평균 및 최악 실행 시간: O(n²)
메모리(공간 복잡도): O(1)