📌 세그먼트 트리란?
오늘은 트리 영역에서 중요한 개념인 세그먼트 트리(Segment Tree)에 대해서 알아봅니다. 세그먼트 트리는 연속적으로 존재하는 여러 개의 데이터를 특정한 구간의 정보(최솟값, 최댓값, 합 등)을 저장하기 위한 트리입니다. 이진 트리의 형태를 지니며, 특정 구간에 대한 합을 가장 빠르게 구할 수 있습니다.
📌 세그먼트 트리 예시와 구현
예시 데이터 : 1부터 15까지의 자연수
위와 같이 1부터 15까지의 데이터가 있다고 가정합니다. 우선 데이터를 배열로 표현하면

해당 배열의 원소는 15개이고, 인덱스는 0~15까지 구성됩니다. 만약 인덱스 1부터 7까지의 원소 중 최솟값을 구하게 되면, 1 ~ 7 범위의 원소를 비교하여 최솟값을 가져오면 됩니다. 결과는 2입니다. 이러한 방식으로 특정 구간에 대한 최솟값을 구한다고 고려했을 때, 데이터의 개수가 N개 이면 시간 복잡도는 O(N)이 됩니다. 이러한 방식은 속도가 느리기 때문에 세그먼트 트리를 이용합니다.
배열을 이용하여 특정 구간에 대한 정보( 최솟값 등 )을 구하는 시간 복잡도는 O(N)이다.
⚫ 트리 구조를 이용하여 구하기
우선 기존의 배열을 트리구조로 표현하면 아래 그림과 같습니다.
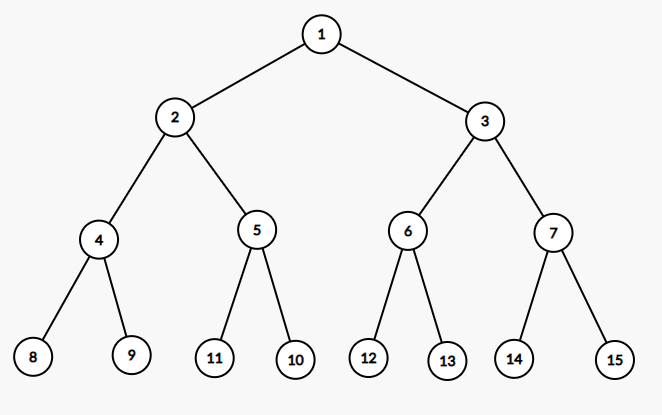
이제 빠르게 구간의 최솟값을 구하기 위해서 '구간 최소 트리'를 새롭게 만들어야 합니다. 먼저 최상단 노드에는 전체 원소 중 최솟값이 들어갑니다. 이후 최상단 노드의 왼쪽 자식인 두 번째 노드에는 인덱스 0~7까지 원소 중 최솟값이 저장되고, 최상단 노드의 오른쪽 자식인 세 번째 노드에는 인덱스 8~15까지 원소 중 최솟값이 저장됩니다.
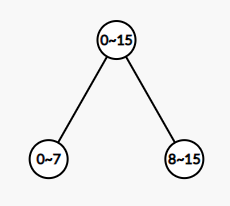
이는 원래 데이터의 범위를 절반으로 나누어서 구간의 최솟값을 저장하도록 하는 것입니다. 해당 과정을 마지막까지 수행하면 전체 데이터의 모든 범위에서의 최솟값이 트리에 저장됩니다.
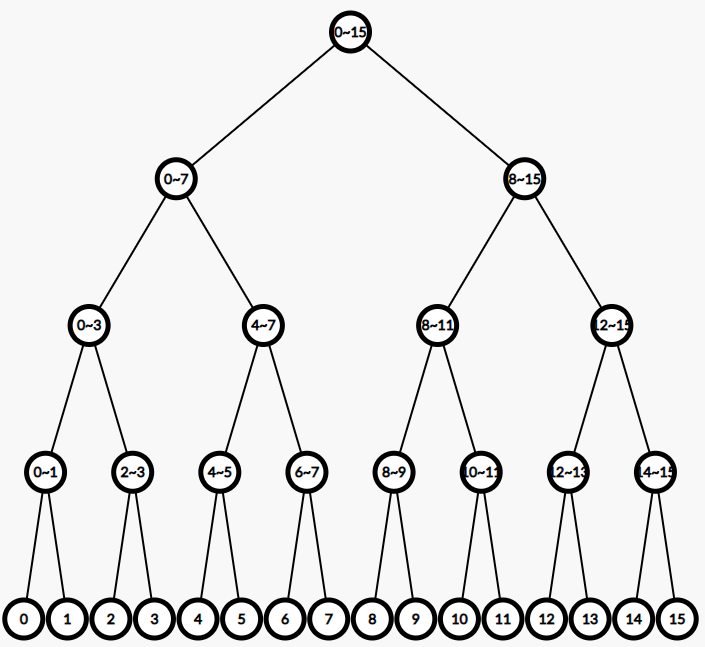
구간 최소 트리는 재귀적으로 구현할 수 있습니다.
int min_segment_tree(int start, int end, int node)
{
if (start == end)
return tree[node] = v[start];
int mid = (start + end) / 2;
return tree[node] = min(min_segment_tree(start, mid, node * 2), min_segment_tree(mid + 1, end, node * 2 + 1));
}원래 15개의 데이터를 가지고 있는 배열에서 구간 최소 트리를 생성하였더니 31개의 원소를 가지게 되는 것을 볼 수 있습니다. 구간 트리를 생성 할 때는 데이터의 개수가 N개일 때 N보다 큰 가장 가까운 N의 제곱수를 구한 뒤에 그것의 2배 크기의 공간이 세그먼트 트리에는 필요합니다. 예제 데이터의 경우 N이 15으로 가장 가까운 제곱수는 16이기 때문에 그것의 2배인 32만큼의 크기가 필요하다는 뜻입니다. 따라서 실제로 세그먼트 트리를 생성할때에는 실제 데이터의 크기인 N에 4배를 곱한 크기만큼의 공간을 구간 트리에 할당합니다.
세그먼트 트리는 데이터의 범위에 대한 정보를 트리 구조로 저장하고 있기 때문에 구간에 대한 데이터를 탐색하는 데에 들이는 비용이 O(logN)입니다. 선형 구조인 배열에 비해 더 빠른 속도로 구간에 대한 정보를 탐색 가능합니다.
세그먼트 트리를 이용하여 특정 구간에 대한 정보 ( 최솟값 등 )을 구하는 시간 복잡도는 O(logN)이다.
📌 세그먼트 트리를 이용하여 구간 최솟값 구하기
이제 구해진 세그먼트 트리를 이용하여 정해진 구간의 최솟값을 구하는 함수를 만들어 보겠습니다. 세그먼트 트리를 이용하기 때문에 구간 최소를 구하는 비용은 당연히 O(logN)입니다.
예를 들어 인덱스 6부터 10까지의 원소 중 최소 값을 구해보려 합니다. 그러면 다음과 같이 세 값 중 최소를 구해주면 됩니다.
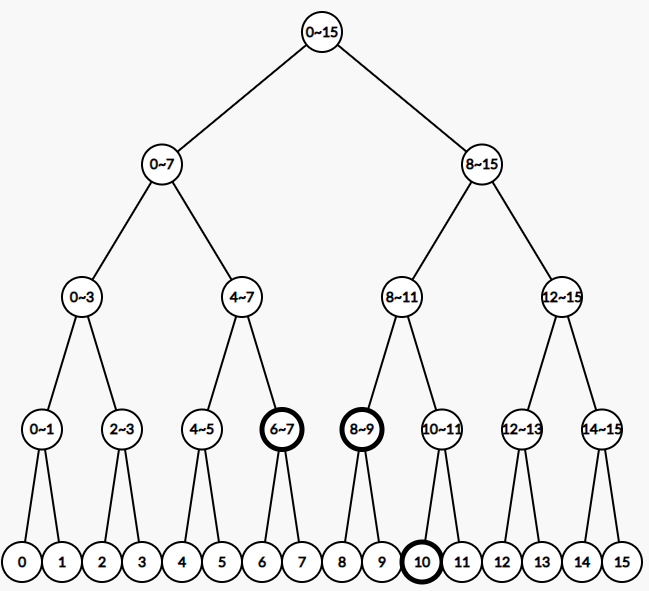
해당 데이터의 경우, 정렬되어 있는 배열이기 때문에 인덱스 6에 해당하는 원소 7이 최솟값이 됩니다. 그러나 데이터가 정렬되어 있지 않은 경우에도 당연히 세그먼트 트리를 이용하여 구간에 대한 정보를 추출할 수 있습니다. 구간의 최소를 구하는 함수는 재귀적으로 작성할 수 있습니다. 구간에 해당하지 않는 범위 같은 경우는 고려하지 않으면 되겠습니다.
int find_min(int start, int end, int node, int left, int right)
{
if (left > end || right < start)
return LONG_MAX;
if (left <= start && end <= right)
return tree[node];
int mid = (start + end) / 2;
return min(find_min(start, mid, node * 2, left, right), find_min(mid + 1, end, node * 2 + 1, left, right));
}
📌 마무리
오늘은 트리 영역에서의 중요한 개념 중 하나인 세그먼트 트리에 대해 알아보았습니다. 세그먼트 트리는 데이터에서 구간에 대한 정보를 탐색, 연산 할 때 유용한 자료구조입니다. 선형 구조를 가진 데이터에 대한 범위 계산과 세그먼트 트리를 이용한 범위 계산의 시간 복잡도를 비교하면서 마치겠습니다.
선형구조를 이용한 데이터 범위 탐색, 연산 : O(N)
세그 먼트 트리를 이용한 데이터 범위 탐색, 연산 : O(logN)


데이터 변경 - 수정에 대한 사항은 추후 업데이트 예정입니다.