강의의 intro부터 굉장히 찔렸던 점이 있다.
대부분의 사람들이 이론을 공부하고 그에 대한 이해를 바탕으로 구현을 하는 게 아니라,
구현한 코드를 먼저 보면서 이론을 이해한다는 것이다.
효과가 없고, 좋지 않은 방식이라고 하는데
내 공부 방식도 처음에는 이론을 배우려고 하다가 항상 끝에는 저렇게 흘러갔던 것 같다.
강의를 계속 들으며 공부 방식을 고칠 수 있기를 기원한다.
자료구조란 무엇인가?
프로그램==데이터의 표현+데이터의 처리.
여기서
데이터의 표현==자료구조,
데이터의 처리==알고리즘이다.
알고리즘은 사실 자료구조에 의존한다.
이는 코드를 작성하며 누구나 느낄 것이다.
내가 쓰고 있는 변수와 데이터들의 특징을 알아야 그에 알맞은 대처를 하며 코드를 작성할 수 있다.
따라서 자료구조를 이해하는 것이 중요하다.
알고리즘의 성능분석 방법
시간 복잡도, 즉 얼마나 연산을 많이 하느냐가 알고리즘의 성능분석 평가에 지배적이다.
즉 연산 횟수를 함수로 표현한 T(n)이 성능분석의 평가 지표이다.
이 T(n)을 하나로 정의하기는 쉽지 않다.
상황에 따라 T(n)이 바뀌는데, 이 상황을 주로 3가지로 나눈다.
- 최상의 경우
-운이 좋게, 한 번의 연산만으로 프로그램을 짠 목적을 달성하는 경우이다. - 평균적인 경우
-일반적으로 등장하는 경우이다. - 최악의 경우
-운이 나쁘게도 최대의 연산을 했으나 목적을 달성하지 못한 경우이다.
최상의 경우는 상정하지 않는 게 낫고, 평균적인 경우는 T(n)을 측정하기가 굉장히 복잡하기 때문에 보통 최악의 경우로 T(n)을 구한다.
배열 탐색 알고리즘
순차 탐색 알고리즘
-배열의 첫 번째부터 마지막까지 순차적으로 target을 찾아보는 방식
-T(n)=n (n: 배열의 크기)
이진 탐색 알고리즘
-정렬된 배열의 중앙이 target인지 보고, 좁혀진 범위 안에서 다시 중앙을 target과 비교해 나가는 방식
-T(n)=log2(n)
(본래 Log2(n)+1이지만, 바로 뒤에 나올 '빅-오'개념에 따라 +1을 생략한다)
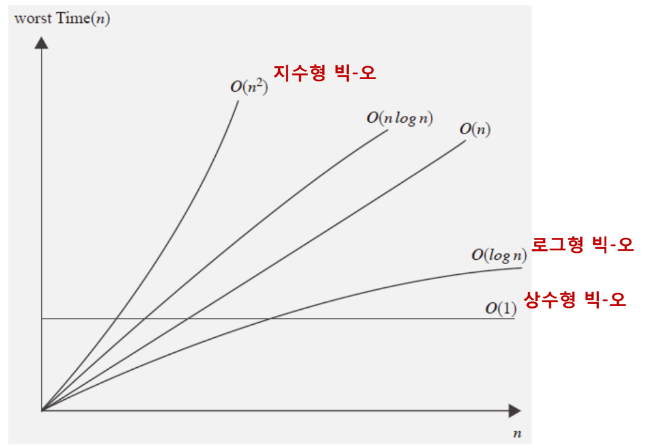
빅-오(Big-Oh) 표기법
'빅-오'는 T(n)에서 실제로 영향력 있는 부분을 말한다.
T(n)이 다항식일 경우 빅-오는 최고차항에서 계수를 생략한 부분이다.
예를 들어 T(n)=5n^3+10n+4 일 경우, 빅-오는 n^3이다.
상당히 간단하다!
이 빅-오를 고려한 관점으로 보면,
순차 탐색 알고리즘보다 이진 탐색 알고리즘이 우수하다고 볼 수 있다.
(연산횟수 증가율을 봤을 때, 순차 탐색 알고리즘이 언젠가는 반드시 이진 탐색 알고리즘을 뛰어넘을 것이기 때문이다. )