Chapter 02는 재귀에 대해 다룬다.
재귀함수의 호출 원리
void Recursive(void){
printf("Recursive call!\n");
Recursive();
}이라는 재귀 호출 코드가 있다고 해 보자.
여기서 재귀 함수의 원리는 Recursive()를 통해 위 함수에 재진입한다는 의미보다는,
'호출하는 만큼 복사본이 만들어진다'
로 이해하는 것이 좋다.
나는 자기 스스로를 계속 호출하면서 마지막 복사본까지 호출을 마치면,
이제 마지막에서 처음으로 거슬러 올라가면서 실행을 하며 차례차례 종료한다고 이해했다.
참고로 재귀 호출을 사용할 때는 탈출 조건(재귀 호출을 그만하도록 하는!)을 명시하는 게 중요하다.
그렇지 않으면 무한 복사&실행이 될 것이다.
재귀적 구현의 사례
팩토리얼
int Factorial(int n){
if(n==0)
return 1;
else
return n*Factorial(n-1);
}계속해서 Factorial(현재-1)을 호출하면서 n(n-1)(n-2)...*1 을 계산할 수 있는 것이다.
피보나치 수열
피보나치 수열은 알다시피 첫 두 요소는 0,1 이고, 그 다음부터는 전의 2개를 더해가면서 수열을 만들어 가는 것이다.
0, 1, 1, 2, 3, 5, 8, 13, ...
int Fibo(int n){
if(n==1)
return 0;
else if(n==2)
return 1;
else
return Fibo(n-1)+Fibo(n-2);
}이진 탐색 알고리즘
이전 CH01포스팅에서 살펴봤던 이진 탐색 알고리즘 또한 재귀적으로 구현 가능하다.
중간을 살펴보고, 아니면 반 잘라서 또 중앙을 보고, ... 특정한 패턴이 반복되지 않는가?
int BSearchRecur(int ar[],int first, int last, int target){
if(first>last)
return -1;
int mid=fr=(first+last)/2;
if(ar[mid]==target)
return mid;
else if(ar[mid]>target)
BSearchRecur(ar, first, mid-1,target);
else
BSearchRecur(ar,mid+1,last,target);
}하노이 타워
하노이 타워는 코드로 구현하기에 왠지 복잡할 것 같지만,
재귀의 원리를 이용하면 꽤 간단한 코드가 나온다.
그러나 오히려 코드가 간단하기에 그 원리를 이해 못하는 경우도 있다.
먼저, 하노이 타워란
1번 타워에 순차적으로 쌓여 있는 원반을 3번 타워로 이동시키는 문제이다.
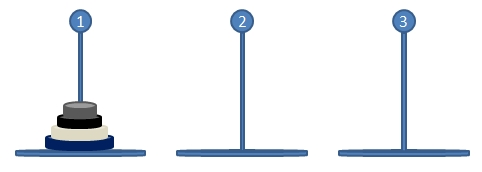
원반은 한 번에 1개만 움직일 수 있으며,
큰 원반이 작은 원반의 위에 있는 상황이 생겨서는 안 되며,
중간에 있는 B타워를 이용할 수 있다.
나는 이 하노이 타워의 알고리즘을 '의뢰'로 이해했다.
예를 들어 원반 4개를 옮기는 문제라고 하면,
원반 4개를 옮기는 의뢰를 맡은 사람 A가 '위에 3개만 누가 2번 타워로 옮겨 준다면 내가 마지막 원반을 3번타워로 옮기고 2번타워에 있는 것들을 3번타워로 옮기면 되니, 문제가 쉬워질 텐데..'하고 원반 3개를 옮기는 새끼 의뢰를 맡기는 것이다.
그러면 원반 3개를 옮기는 의뢰를 맡은 사람 B가 똑같이 '위에 2개만 누가 옮겨 준다면...'
이런 식으로 새끼 의뢰가 계속 진행되어,
결국 원반 4개를 옮기는 문제는 원반 1개를 옮기는 문제까지 축소될 수 있다는 것이다.
void HanoiTowerMove(int num, char from, char by, char to){//원반 n개를 옮기는 문제
if(num==1) //탈출 조건: 맨 아래에 있는 원반만 남았다면
printf("원반 1을 %c에서 %c로 이동\n", from, to);
else{
HanoiTowerMove(num-1,from,to,by)//1. 누가 위에 (n-1)개만 중간 타워로 옮겨 준다면
printf("원반%d를 %c에서 %c로 이동\n", num, from, to)//2. 내가 마지막 원반을 목적지로 옮기고
HanoiTowerMove(num-1,by,from,to)//3. 2번타워에 있는 것들을 3번 타워로 옮기면 되니
}
}
