[ML] Supervised Learning // Linear Regression_1

Yeon·2023년 12월 1일

ML

목록 보기

1/7

Supervised Learning

Data : $D = {d^{(1)} , d^{(2)},... ,d^{(N)}}$ , a set of N examples $d^{(N)} = (x^{(n)}, y^{(n)})$
- $x^{(n)}$ is input vector, $y^{(n)}$ is output vector
Goal : X -> Y
입력 데이터에 대한 정답이 함께 주어진다.
Input data를 받아서 그것에 해당하는 정답 Label을 정보로 입력받는다.
두개의 대표적인 문제
- Regression : $X$ is dicrete or continous -> $Y$ is continous
- Classification : $X$ is discrete or continuous -> $Y$ is discrete

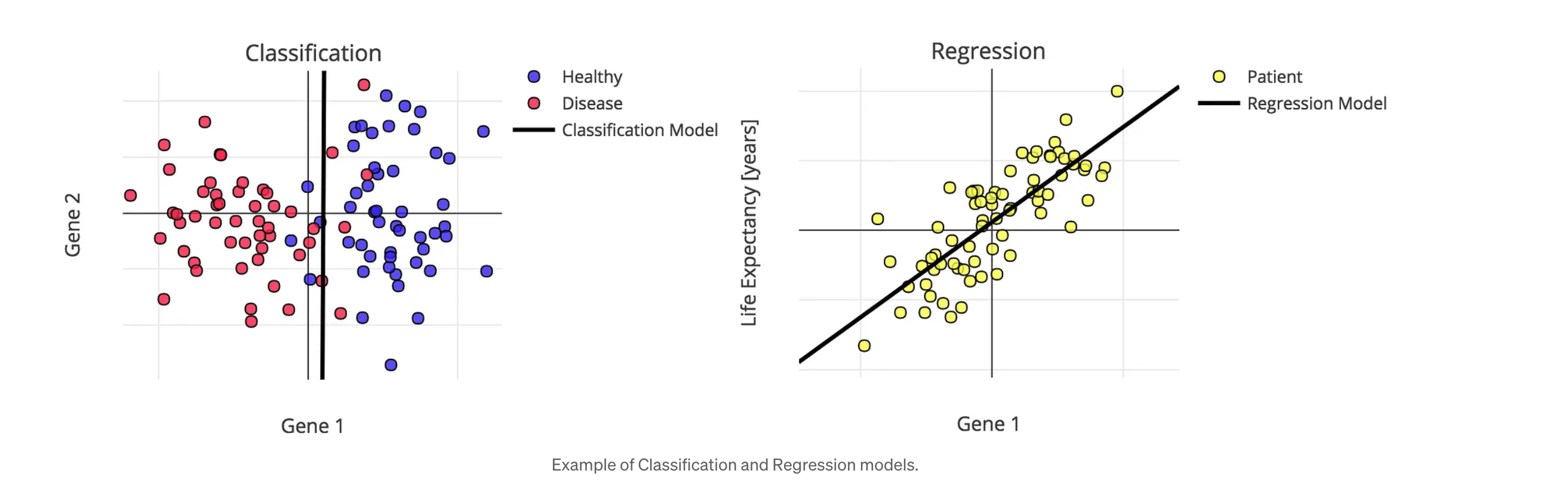
Regression

$X$ : Input variable(vector)
- $x$ : Input value(vector)
- $x^{(n)}$ : Input value of the n-th instance
- $x_{j}^{(n)}$ : j-th attribute (column) of the n-th instance
$Y$ : Output variable(scalar)
- $y$ : Output value
- $y^{n}$ : Output value of the n-th instance
$D$ : Dataset
- d : Input dimensionality
Regression : Y is continouous
- X의 값이 주어지면 target Y의 값을 예측하는 것이다.
- X : 독립변수이고, features, predictors
- Y : 종속변수이고, outcome을 나타낸다.
- 쉽게 말해서, X와 Y의 관계를 예측한다고도 말할 수 있다.
Regression as a function approximator
- Degree가 높아질수록 모델의 복잡성은 높아지고 에러는 줄어든다.
- 그러나, 여기서 고민해봐야할 것이 모델이 너무 복잡해지면, Overfitting이 발생할 가능성이 높다. 또, 모델이 너무 간단해지면, Underfitting이 발생할 가능성이 높다.
Y is a linear Combination of input components
- $f(x) = w_0 + w_1x_1 + w_2x_2 + ... + w_dx_d = w_0 + \sum_{j=1}^{d} {w_jx_j}$
- $w_0, w_1, w_2, ... , w_d$ - parameters(weights) -> parametric method
- 주어진 x,y를 정확하게 예측하는 w를 찾아야 한다.
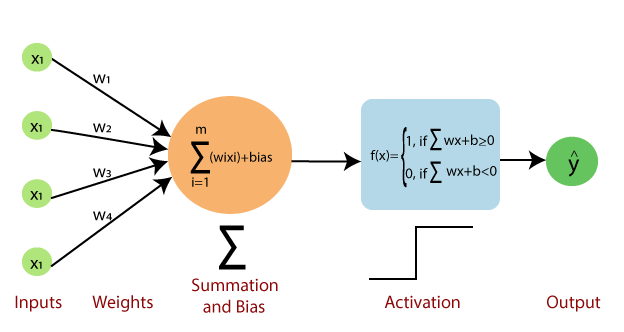
모델을 학습시키는 방법
1. Model을 선택한다
  - Select a model or a set of models(with parameters) $y = ax +b$
2. Choose the objective (error) function
  - Mean Squared Error $Error(D,a,b) = \frac{1}{N}\sum_{n=1}^{N} {(y^{(n)} - (ax^{(n)} + b))}^2$
3. Learning
  - Find the set of parameters(a,b) minimizing the error function on $D_{train}$
  - $(a^*,b^*) = argmin_{(a,b)}Error(D,a,b)$
  - argmin : 주어진 함수나 표현식을 최소화하는 변수의 값을 찾는 연산이다. 쉽게 말해 최소값을 주는 입력값들을 찾는 것을 의미함. Linear Regression에서는 최소의 Error값을 갖는 a,b값을 찾는 것을 의미한다.
4. Testing/Validation
5. Application
  - Apply the learned model to new data $f(x) = a^*x + b^*$

Intercept

$( x_0 )$ 가 1로 설정되는 이유는 선형 회귀 모델에 상수항(절편, intercept) $( w_0 )$ 를 포함시키기 위함입니다. 선형 회귀 모델은 일반적으로 다음과 같은 형태를 가집니다:

$y = w_0 + w_1x_1 + w_2x_2 + \ldots + w_dx_d$

여기서 $( w_0 )$ 는 절편을 나타내며, $( x_1, x_2, \ldots, x_d )$ 는 특성들을 나타냅니다. 모델을 행렬 방정식의 형태로 나타낼 때, 우리는 각 데이터 포인트에 대해 특성 벡터를 다음과 같이 확장합니다:

$\mathbf{x}^{(n)} = [1, x_1^{(n)}, x_2^{(n)}, \ldots, x_d^{(n)}]$

이 때 첫 번째 항목인 1은 $( w_0 )$ 에 곱해져서 절편이 되고, 나머지 항목들은 해당 특성의 가중치와 곱해집니다. 따라서 $( x_0 )$ 을 1로 설정하는 것은 모델에 절편 항을 포함시키기 위한 계산상의 편의를 제공합니다.

이러한 접근 방식을 사용하면, 모든 특성과 가중치를 일관된 방식으로 처리할 수 있으며, 행렬 연산을 사용하여 모델을 더 쉽게 계산할 수 있습니다. $( x_0 )$ 을 모든 데이터 포인트에 대해 1로 설정함으로써, 절편 $( w_0 )$ 는 항상 모델에 포함되고, 행렬 연산에서 자연스럽게 처리됩니다.

또한, 선형 회귀 모델에서 독립 변수(특성)가 모두 0일 때, 종속 변수(목표 변수)의 예측값을 나타냅니다.

절편 없이 모델을 표현할 경우 : 만약 모델에서 절편을 생략한다면, 모델의 예측은 항상 원점을 통과해야 합니다. 즉, 모든 독립 변수의 값이 0일 때, 종속 변수의 예측값도 0이 되어야 합니다. 그러나, 실제 우리가 사용하는 데이터에는 적합하지 않은 경우가 많습니다.
절편을 포함한 모델의 표현 : 절편을 포함함으로써 모델은 데이터의 중심이 원점에서 벗어날 수 있게 되고, 데이터의 실제 분포를 더 잘 반영할 수 있게 됩니다. 절편은 데이터가 가지고 있는 평균적인 경향성을 잡아주는 역할을 하며, 모델이 다른 변수들의 영향을 받지 않는 상수 값을 가질 수 있게 합니다.

Error Function

Quantifies the mean-squared error that measures how much our predictions deviate from the desired answers.
$Error J(w,D) = \frac{1}{N}\sum_{n=1}^{N} {(y^{(n)} - (f(x^{(n)}, w))}^2$
Learning
- $min J(w,D)$ : Finding weights w that minimizing the error.

평균 제곱 오차 (MSE)

이 슬라이드에서 제시된 MSE는 다음과 같습니다:

$J(\mathbf{w}) = \frac{1}{N} \sum_{n=1}^{N} (y^{(n)} - \mathbf{w}^T\mathbf{x}^{(n)})^2$

여기서:

$J(\mathbf{w})$ 는 손실 함수입니다.
$( N )$ 은 데이터 포인트의 개수입니다.
$( y^{(n)} )$ 은 ( n )번째 데이터 포인트의 실제 값입니다.
$( \mathbf{x}^{(n)} )$ 은 ( n )번째 데이터 포인트의 입력 벡터입니다.
$( \mathbf{w}^T\mathbf{x}^{(n)} )$ 는 ( n )번째 데이터 포인트에 대한 모델의 예측값입니다.

가중치에 대한 오차의 미분

최적화 과정에서는 이 손실 함수를 $( \mathbf{w} )$ 에 대해 미분합니다. 이 미분 연산은 각 가중치 파라미터에 대한 손실 함수의 기울기를 계산하여, 가중치를 조정해야 할 방향을 결정합니다. $( \mathbf{w} )$ 에 대한 $( J )$ 의 편미분은 다음과 같습니다:

$\frac{\partial J}{\partial w_j} = - \frac{2}{N} \sum_{n=1}^{N} (y^{(n)} - \mathbf{w}^T\mathbf{x}^{(n)}) x_j^{(n)}$

여기서 $( w_j )$ 는 가중치 벡터의 $( j )$ 번째 요소입니다.

기울기 벡터

전체 가중치 벡터 $( \mathbf{w} )$ 에 대한 손실 함수의 기울기는 다음과 같은 벡터로 표현됩니다:

$\nabla_{\mathbf{w}} J(\mathbf{w}) = - \frac{2}{N} \sum_{n=1}^{N} (y^{(n)} - \mathbf{w}^T\mathbf{x}^{(n)}) \mathbf{x}^{(n)}$

이 벡터의 각 요소는 손실 함수를 해당 가중치로 편미분한 것임. 최적화 과정에서는 이 기울기 벡터가 $\mathbf{0}$ 이 되는 지점을 찾음. 이 지점이 바로 손실 함수의 최소값을 주는 지점, 즉 모델의 최적 파라미터가 됨.

최적화 과정

기울기 계산: 데이터 포인트에 대해 손실 함수의 기울기를 계산함.
가중치 업데이트: 경사 하강법 같은 최적화 알고리즘을 사용하여 이 기울기를 바탕으로 가중치를 조정함.
반복: 이 과정을 반복하여 손실 함수를 최소화하는 가중치 $(\mathbf{w} )$ 를 찾음

이 최적화 과정은 모델이 데이터를 잘 나타낼 수 있도록 가중치를 조절하는 데 필수적이며, 이를 통해 예측의 정확도를 높일 수 있습니다.

체인 룰의 활용 예

선형 회귀의 손실 함수를 미분할 때 체인 룰이 사용됩니다. 예를 들어, 가중치 $( w_j )$ 에 대한 손실 함수 $( J(\mathbf{w}) )$ 의 편미분 :

$J(\mathbf{w}) = (y - \mathbf{w}^T\mathbf{x})^2$
이 경우, $( u = y - \mathbf{w}^T\mathbf{x} )$ 라는 내부 함수와 $( f(u) = u^2 )$ 라는 외부 함수로 생각함. 체인 룰을 적용하여 $( w_j )$ 에 대한 $( J )$ 의 편미분 :

$\frac{\partial J}{\partial w_j} = \frac{\partial J}{\partial u} \cdot \frac{\partial u}{\partial w_j}$

$\frac{\partial J}{\partial u} = 2(u)$
$\frac{\partial u}{\partial w_j} = -x_j$

결과적으로, 체인 룰을 적용한 편미분 :

$\frac{\partial J}{\partial w_j} = 2(y - \mathbf{w}^T\mathbf{x})(-x_j)$

체인 룰은 미분을 계산할 때 내부 함수의 미분계수와 외부 함수의 미분계수를 연쇄적으로 곱하는 방법으로, 복잡한 함수의 미분을 단순화하는 데 유용합니다.

Solving the Optimization Problem

최적화 문제를 해결하기 위해 손실 함수인 평균 제곱 오차의 그라디언트를 가중치 벡터 $( \mathbf{w} )$ 에 대해 0으로 설정합니다. 이것은 선형 방정식의 시스템을 생성하는데, 이 시스템은 $( d + 1 )$ 개의 가중치 $( \{w_0, w_1, ..., w_d\} )$ 를 구하기 위한 방정식을 포함하고 있습니다.

선형 방정식 시스템(System of Linear Equations, SLE)은 다음과 같이 행렬 형태로 표현됩니다:

$[ \mathbf{A}\mathbf{w} = \mathbf{b} ]$

여기서:

$( \mathbf{A} )$ 는 설계 행렬로, 각 데이터 포인트에 대한 특성 값들과 각 데이터 포인트에 대해 1을 포함하는 첫 번째 열(절편을 위한)을 가진 $( n \times (d+1) )$ 행렬입니다.
$( \mathbf{w} )$ 는 찾고자 하는 가중치 벡터입니다.
$( \mathbf{b} )$ 는 실제 목표 값 $( y )$ 를 포함하는 벡터입니다.

그라디언트가 0인 조건에서, 이 시스템은 정규 방정식(normal equations) ( $(\mathbf{X}^T\mathbf{X})\mathbf{w} = \mathbf{X}^T\mathbf{y} )$ 로 변환될 수 있습니다. 이 방정식은 $( \mathbf{w} )$ 에 대한 해를 제공합니다 :

$\mathbf{w} = (\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T\mathbf{y}$

여기서:

$\mathbf{X}$ 는 각 데이터 포인트에 대한 특성 값을 포함하는 $n \times d$ 데이터 행렬입니다. 추가적으로 각 데이터 포인트에 대해 1을 포함하는 열이 있습니다.
$\mathbf{y}$ 는 각 데이터 포인트의 실제 값 $y$ 를 포함하는 벡터입니다.
$\mathbf{w}$ 는 가중치 벡터로, 이 식을 사용하여 계산할 수 있습니다.