🔍다익스트라 (Dijkstra)
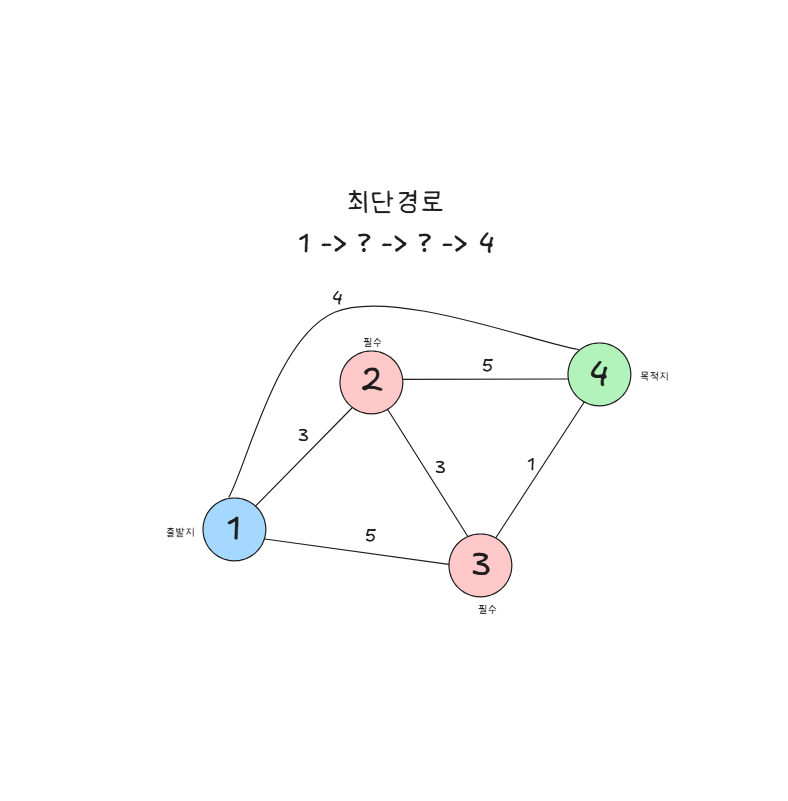
다익스트라 알고리즘은 그래프 내의 한 정점에서 출발해서 목적지 정점까지 가는 가장 짧은 경로를 찾아주는 알고리즘입니다
📌다익스트라 알고리즘의 사용 조건
다익스트라 알고리즘은 다음 조건들을 만족할 때 사용할 수 있습니다
- 음의 가중치가 없는 그래프: 음수 가중치를 포함하지 않는 경우만 적용할 수 있습니다
📌 다익스트라 알고리즘의 동작 방식
다익스트라 알고리즘은 다음과 같은 단계로 작동합니다
- 초기화
- 시작 정점의 거리를 0으로 설정하고, 나머지 모든 정점의 거리는 무한대로 설정합니다
- 시작 정점을 우선순위 큐(Priority Queue)에 넣습니다
- 최소 거리 정점 선택
- 아직 방문하지 않은 정점 중에서 현재까지의 거리가 가장 짧은 정점을 선택합니다.
- 주변 정점 거리 갱신
- 선택한 정점에서 인접한 정점들로 가는 거리를 확인하고, 기존의 거리보다 짧은 경로를 발견하면 갱신합니다
- 이때 갱신된 정점은 다시 우선순위 큐에 추가합니다
- 반복
- 우선순위 큐가 비워질 때까지 위의 과정을 반복합니다
이 과정을 통해 목적지 정점까지의 최단 경로를 계산합니다
📌 다익스트라 알고리즘의 장점
- 빠른 속도와 효율성: 우선순위 큐와 함께 구현하면 시간 복잡도가 O(E log V)로 매우 효율적입니다 (E: 간선의 수, V는 정점의 수)
📌 다익스트라 알고리즘의 단점
- 음수 가중치 불가: 음의 가중치가 있는 경우에는 사용할 수 없습니다
🚀 다익스트라 알고리즘이 적용된 문제
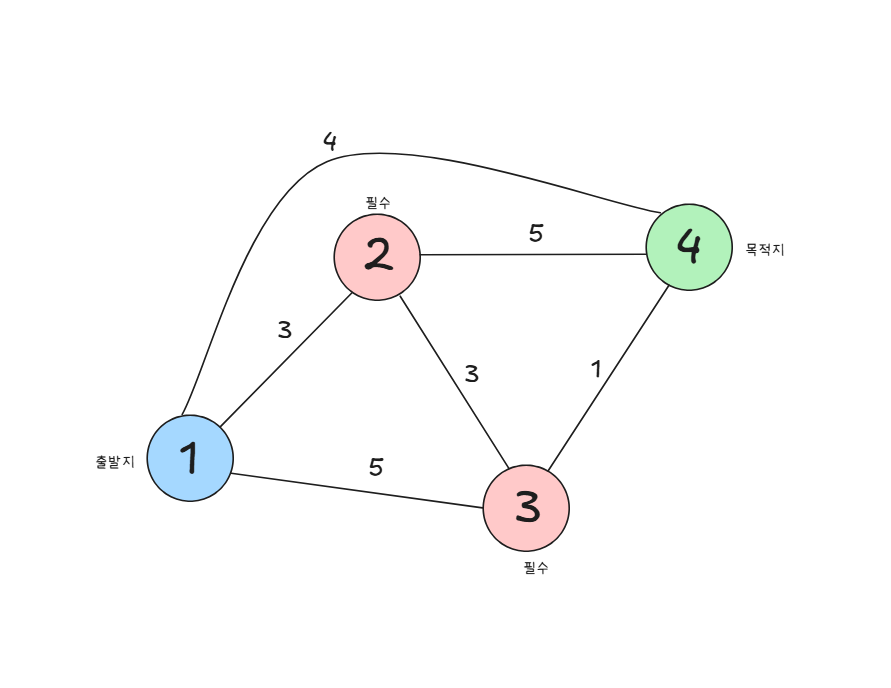
백준 1504번: 특정한 최단 경로 문제는 다익스트라 알고리즘을 활용하여 해결할 수 있는 대표적인 문제입니다
이 문제는 출발점에서 목적지까지 이동하는 최단 경로를 구하는 문제로,
다음과 같은 추가 조건을 만족해야 합니다
- 주어진 두 정점(a, b)을 반드시 거쳐야 합니다
음의 가중치가 없는 그래프가 주어졌습니다
따라서 최단거리를 구하기 위해 다익스트라 알고리즘으로 해결할 수 있습니다
이 문제는 두 가지 경로로 접근할 수 있습니다
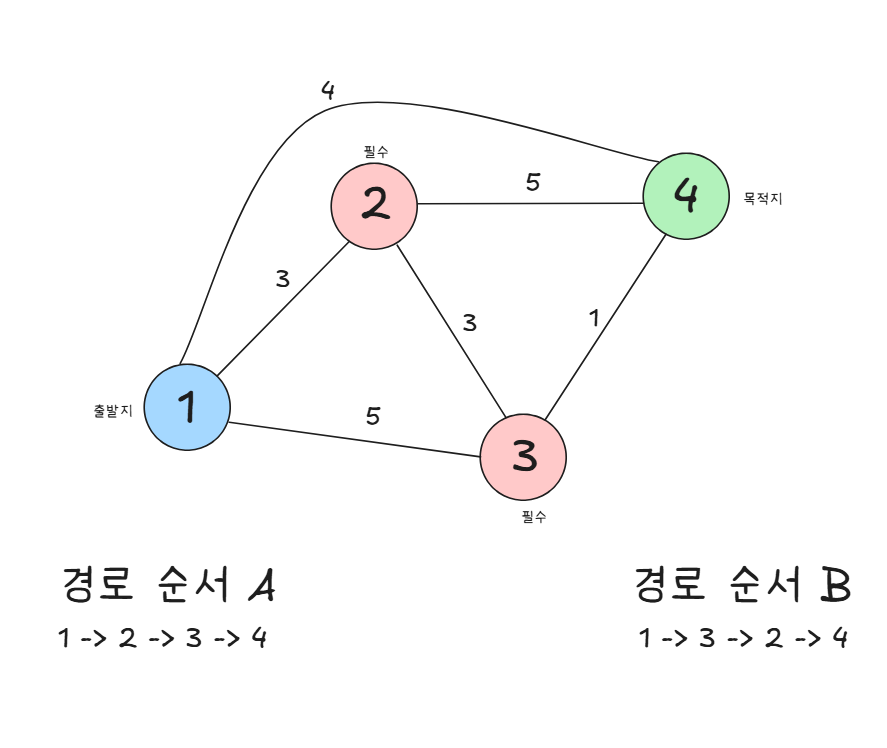
출발지 -> a지점 -> b지점 -> 도착지출발지 -> b지점 -> a지점 -> 도착지
각 구간마다 다익스트라 알고리즘을 통해 최단거리를 계산하고
두 경로 중 최소값을 선택하면 정답을 구할 수 있습니다
int count1 = dijkstra(1,a) + dijkstra(a,b) + dijkstra(b, n);
int count2 = dijkstra(1,b) + dijkstra(b,a) + dijkstra(a, n);이어서 다익스트라 알고리즘을 구현했습니다
private static int dijkstra(int start, int end) {
Arrays.fill(dist, INF);
visited = new boolean[n+1];
PriorityQueue<int[]> pq = new PriorityQueue<>((o1,o2) -> o1[1] - o2[1]);
pq.add(new int[]{start, 0});
dist[start] = 0;
while(!pq.isEmpty()){
int[] now = pq.poll();
if(!visited[now[0]]){
visited[now[0]] = true;
for (int[] cur : lists[now[0]]) {
if(dist[cur[0]] > dist[now[0]] + cur[1]){
dist[cur[0]] = dist[now[0]] + cur[1];
pq.add(new int[]{cur[0], dist[cur[0]]});
}
}
}
}
return dist[end];
}두 경로 중 하나라도 INF보다 작다면 최솟값으로 ans를 갱신합니다
만약 둘다 INF이상이라면 -1이 출력됩니다
static int INF = 200_000_000;
int ans = -1;
if(count1 < INF || count2 < INF) {
ans = Math.min(count1, count2);
}
bw.write(ans+"");이렇게 다익스트라 알고리즘을 적용하여,
조건을 만족시키면서 목적지까지 가는 최단 경로를 얻을 수 있습니다
문제 링크
✍️ 결론
다익스트라 알고리즘은 최단 경로를 빠르고 효율적으로 구하는 알고리즘입니다
하지만 음수 가중치를 처리할 수 없다는 제약이 있으므로,
주어진 그래프의 특성과 조건을 파악하여 적절히 활용해야합니다
