[CS/알고리즘] 플로이드-워셜 알고리즘

황제연·2025년 3월 29일

알고리즘 플로이드 워셜

CS학습

목록 보기

27/193

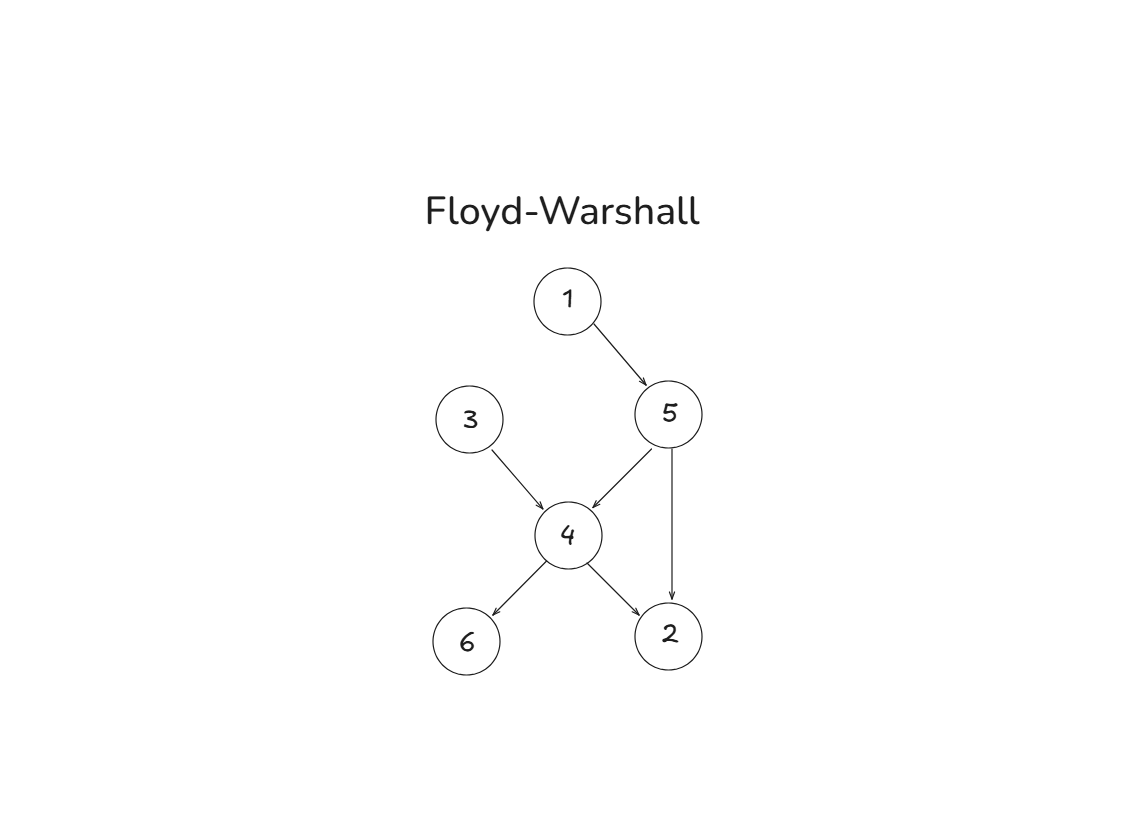
🔍 플로이드-워셜(Floyd-Warshall) 알고리즘

플로이드-워셜 알고리즘은 그래프에서 모든 정점 간의 최단 경로를 찾을 때 사용하는 알고리즘입니다

📌 플로이드-워셜 구현방식

플로이드-워셜 알고리즘은 크게 두 가지 방법으로 구현할 수 있습니다

DP를 이용한 방식
3중 반복문(3중 포문)을 이용한 방식

이번 글에서는 3중 포문 방식으로 구현하는 방법에 대해 정리했습니다

🛠️ 플로이드-워셜 동작 방식

플로이드-워셜 알고리즘의 핵심은 중간 정점(k)을 거쳐 가는 경로가 기존 경로보다 더 짧다면, 그 경로를 선택하는 방식입니다
즉, 모든 정점들을 한 번씩 중간 경유지로 설정해보고, 최단 경로를 반복해서 업데이트합니다

for (int k = 1; k < n+1; k++) { // 중간 정점
    for (int i = 1; i < n+1; i++) { // 출발 정점
        for (int j = 1; j < n+1; j++) { // 도착 정점
            if (list[i][k] + list[k][j] < list[i][j]) {
                list[i][j] = list[i][k] + list[k][j];
            }
        }
    }
}

위 코드를 보면 알 수 있듯이, 플로이드-워셜 알고리즘은 모든 정점 간 조합 (i, j)에 대해서
중간 정점 k를 통해 가는 새로운 경로가 기존보다 짧다면,
이를 최단 경로로 계속해서 갱신하는 방식입니다

📌 플로이드-워셜의 장점

모든 정점 간 최단 경로를 한 번에 계산할 수 있어서 간단하고 효율적입니다

📌 플로이드-워셜의 단점

시간 복잡도가 O(n³)으로 높기 때문에 정점의 수 n이 커질수록 실행 속도가 느려지고 성능이 저하됩니다

🚧 플로이드-워셜 주의사항

알고리즘을 사용하기 전에 반드시 초기 최단 거리를 무한대(INF) 로 설정해야 합니다
다익스트라 알고리즘과 달리 음수 간선(음의 가중치)은 허용되지만, 음수 사이클이 존재하면 사용할 수 없습니다

🚀 플로이드-워셜이 적용된 문제

백준 2458번 - 키 순서 문제는 플로이드-워셜을 적용해 해결할 수 있는 대표적인 문제입니다

이 문제는 자신의 키 순서를 정확히 알기 위해서,
자신과 연결된 정점들의 개수가 자신을 제외한 모든 정점의 개수와 일치해야 합니다

이때, 두 정점 사이가 직접적으로 연결되어 있지 않더라도
다른 정점을 거쳐 간접적으로 연결되었다면 두 정점은 연결된 것으로 판단합니다
이런 연결 여부를 확인하기 위해 플로이드-워셜 알고리즘을 사용할 수 있습니다.

private static void floydWarshall() {  
    for (int k = 1; k < n + 1; k++) {  // 중간 정점
        for (int i = 1; i < n + 1; i++) {  // 시작 정점
            for (int j = 1; j < n + 1; j++) {  // 종료 정점
                if(list[i][k] && list[k][j]){  
                    list[i][j] = true;  
                }  
            }  
        }  
    }  
}

위 코드를 통해 두 정점 간의 간접적인 연결 관계까지 파악할 수 있습니다
이를 바탕으로 문제의 정답을 구할 수 있습니다

이렇게 플로이드-워셜 알고리즘을 활용하면 정점 간의 연결 여부를 확인할 수 있고,
특정 중간 정점을 반드시 거쳐 가는 최단 경로까지도 구할 수 있습니다