서론
알고리즘 문제를 풀면서 DFS 와 Backtracking를 거의 동일한 개념으로 사용했었습니다
이번에는 DFS와 Backtracking의 차이를 명확히 이해하고, 각각의 개념에 대해 정확히 이해할 수 있도록 정리했습니다
DFS
DFS는 Depth-first search의 약자로 그래프 순회에 사용하는 알고리즘입니다
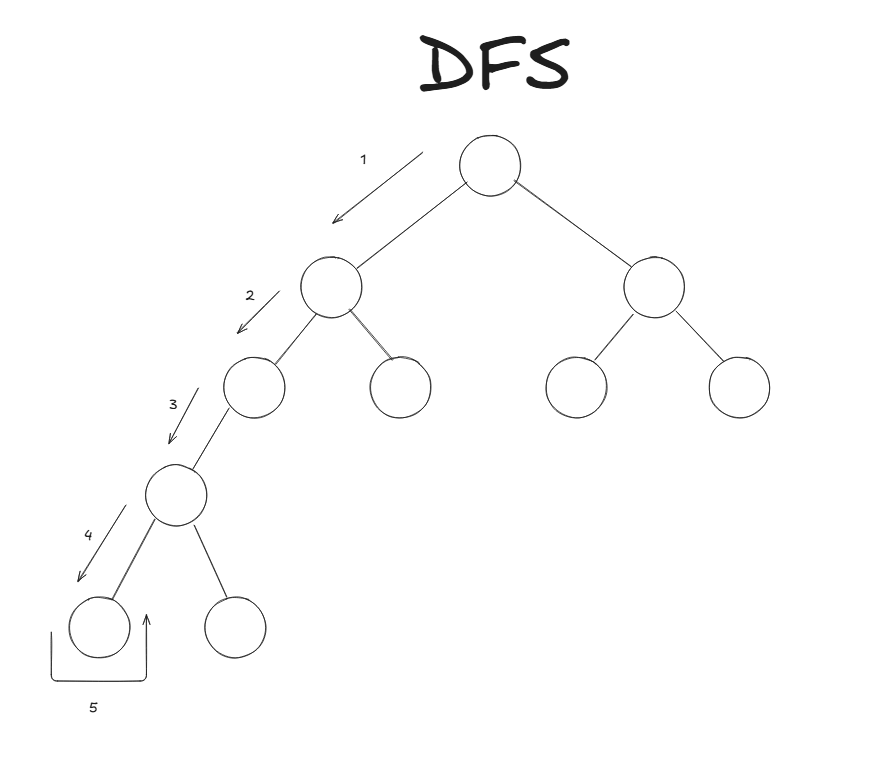
DFS 동작방식
DFS는 루트노드부터 시작해, 연결된 정점을 따라 리프노드까지 탐색한 후,
다시 부모 노드로 돌아와 다른 경로를 탐색하는 방식입니다.
DFS 사용 사례
DFS는 다음과 같은 경우에 주로 사용합니다
- 그래프 탐색
- 경로 찾기
- 사이클 탐지
- 연결 요소 탐지
DFS는 BFS에 비해 공간 효율성을 가진다는 장점이 있습니다.
Backtracking
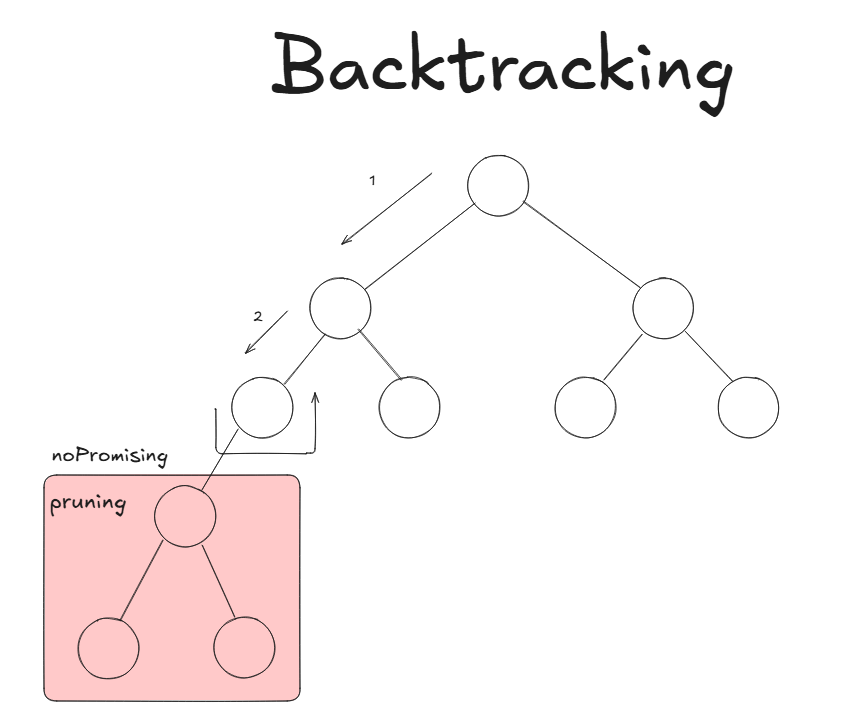
Backtracking 동작방식
Backtracking은 모든 가능한 경우를 탐색하되, 특정 조건을 만족하지 않는 경우에는
더 깊이 탐색하지 않고 되돌아가는 방식입니다
즉, 제약조건을 만족하지 않는 경로는 탐색을 중단해, 불필요한 연산을 줄일 수 있습니다
Backtracking 동작방식 세부
Backtracking의 진행 절차를 더 자세히 살펴보면 다음과 같습니다
1. DFS방식으로 탐색을 시작합니다
2. 다음 탐색할 노드가 유망(Promising)한지 판단합니다
- 유망하다는 것은 탐색할 가치가 있다는 것입니다
3. 유망하다면 탐색을 계속 진행하고, 그렇지 않다면 탐색하지 않습니다
- 유망하지 않은 경우(noPromising), 해당 경로는 더이상 탐색할 필요가 없습니다
4. 유망하지 않은 경로를 제외하는 과정을 Pruning(가지치기)라고 합니다
- 즉, 불필요한 탐색을 제거해, 성능을 최적화합니다
Backtracking은 DFS를 기반으로 하지만 Promising(유망) 여부를 판단하고,
noPromising(유망하지 않음)하면 Pruning(가지치기)해, 연산량을 줄이는 것이 핵심입니다.
Backtracking 사용 사례
Backtracking은 다음과 같은 경우에 사용합니다
- 퍼즐 문제: 스도쿠, N-Queen문제, 틱택토 등
- 조합 및 순열
- 최적의 해를 찾는 문제
일반적으로 조합(Combination)과 관련된 문제에서 Backtracking을 사용합니다
DFS VS Backtracking
둘을 비교하면 다음과 같은 표로 정리할 수 있습니다
| Backtracking | DFS |
|---|---|
| 다양한 자료구조(트리, 배열 등)에서 사용 가능 | 그래프 순회에 특화 |
| 제약조건이 있는 문제해결에 적합 | 그래프에서 모든 경로 탐색 |
| 불필요한 탐색을 가지치기해서 성능 향상 | 리프노드까지 탐색해야 종료 |
정리
- DFS는 그래프 탐색을 위한 알고리즘으로, 루트 노드에서 시작해 리프 노드까지 모든 경로를 탐색합니다
- Backtracking은 제약조건을 만족하는 해를 찾기 위해 불필요한 탐색을 중단하고 가지치기 하는 기법입니다
- DFS는 그래프 탐색, 경로 찾기, 연결요소 탐색, 사이클 탐지 등에 사용됩니다
- Backtracking은 스도쿠, 조합 및 순열, 제약조건이 있는 탐색 문제에서 활용됩니다