알고리즘 (DP, DSF)

jun_grammer·2024년 2월 12일

DP dsf 알고리즘

알고리즘 이론

목록 보기

8/11

DP (동적 프로그래밍)

정의

Dynamic Programming
동적 계획 알고리즘은 그리디 알고리즘과 같이 최적화 문제를 해결하는 알고리즘이다.
동적 계획 알고리즘은 먼저 입력 크기가 작은 부분 문제들을 모두 해결한 후에 그 해들을 이용하여 보다 큰 크기의 부분 문제들을 해결하여, 최종적으로 원래 주어진 입력의 문제를 해결하는 알고리즘이다.
피보나치 수 DP 적용
- 피보나치 수는 부분 문제의 답으로부터 본 문제의 답을 얻을 수 있으므로 최적 부분 구조로 이루어져 있다.

과정

1) 문제를 부분 문제로 분할한다.

Fibonacci(n) 함수는 Fibonacci(n-1)
2) 부분 문제로 나누는 일을 끝냈으면 가장 작은 부분 문제부터 해를 구한다.
3) 그 결과는 테이블에 저장하고, 테이블에 저장된 부분 문제의 해를 이용하여 상위 문제의 해를 구한다.
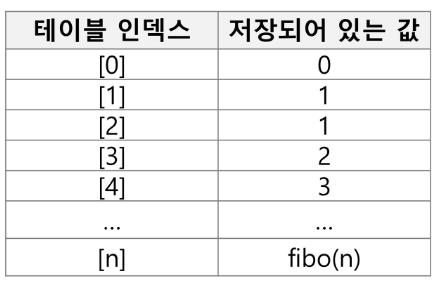
피보나치 수 DP 적용 알고리즘

def lfibo2(n):
    f = [0] * (n + 1)
    f[0] = 0
    f[1] = 1
    for i in range(2, n + 1):
        f[i] = f[i-1] + f[i-2]
    
    return f[n]

DP의 구현 방식
- recursive 방식 : fib1()
- iterative 방식 : fib2()
- memoization을 재귀적 구조에 사용하는 것보다 반복적 구조로 DP를 구현한 것이 성능 면에서 보다 효율적이다.
- 재귀적 구조는 내부에서 시스템 호출 스택을 사용하는 오버헤드가 발생하기 때문이다.

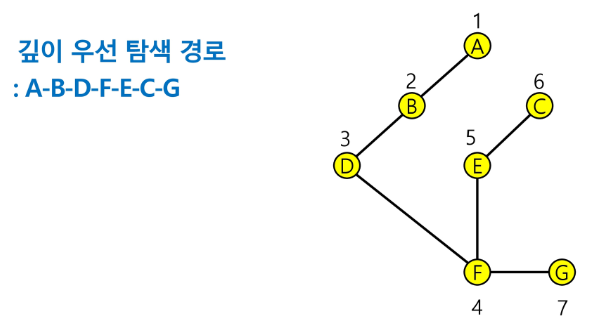
DFS (깊이우선탐색)

비선형구조인 그래프 구조는 그래프로 표현된 모든 자료를 빠짐없이 검색하는 것이 중요함
두 가지 방법
- 깊이 우선 탐색(Depth First Search, DFS) -> 스택을 활용한 탐색만은 아님
- 넓이 우선 탐색(Breadth First Search, BFS)

정의

시작 정점의 한 방향으로 갈 수 있는 경로가 있는 곳까지 깊이 탐색해 가다가 더 이상 갈 곳이 없게 되면, 가장 마지막에 만났던 갈림길 간선이 있는 정점으로 되돌아와서 다른 방향의 정점으로 탐색을 계속 반복하여 결국 모든 정점을 방문하는 순회방법
가장 마지막에 만났던 갈림길의 정점으로 되돌아가서 다시 깊이 우선 탐색을 반복해야 하므로 후입선출 구조의 스택 사용

탐색 과정

1) 시작 정점 v를 결정하여 방문한다.
2) 정점 v에 인접한 정점 중에서
1. 방문하지 않은 정점 w가 있으면, 정점 v를 스택에 push하고 정점 w를 방문한다.
그리고 w를 v로 하여 다시 2)를 반복 한다.
2. 방문하지 않은 정점이 있으면, 탐색의 방향을 바꾸기 위해서 스택을 pop하여 받은 가장 마지막 방문 정점을 v로 하여 다시 2)를 반복한다.
3) 스택이 공백이 될 때까지 2)를 반복한다.

DFS 알고리즘

visited[], stack[] 초기화
DFS(v)
	시작점 v 방문;
    visited[v] <- true;
    while {
    	if (v의 인접 정점 중 방문 안 한 정점 w가 있으면)
        	push(v);
            v <- w; (w에 방문)
            visited[w] <- true
        else
        	if (스택이 비어 있지 않으면)
            	v <- pop(stack);
            else
            	break
	}
end DFS()

예

초기상태 : 배열 visited를 False로 초기화하고, 공백 스택을 생성

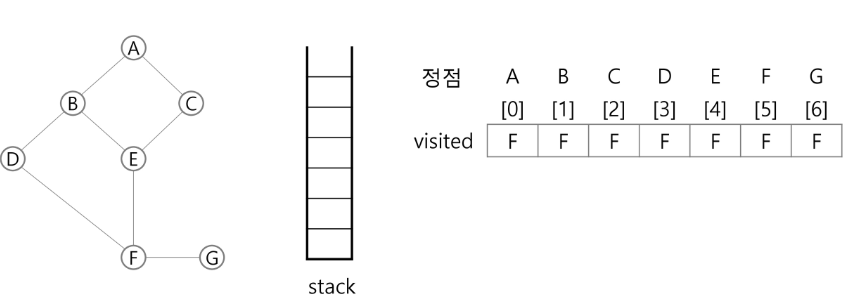
1) 정점 A를 시작으로 깊이 우선 탐색을 시작

A 방문;
visited[A] <- true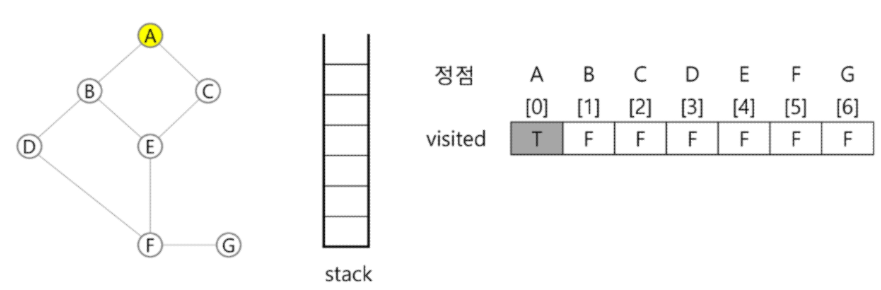

2) 정점 A에 방문하지 않은 정점 B, C가 있이므로 A를 스택에 push 하고, 인접정점 B와 C중에서 오름차순에 따라 B를 선택하여 탐색을 계속한다.

push(A);
B 방문;
visited[B] <- true;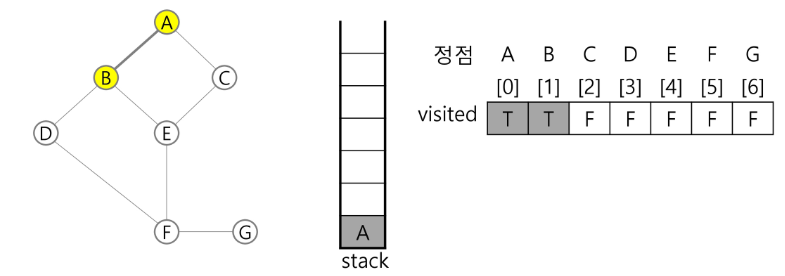

3) 정점 B에 방문하지 않은 정점 D, E가 있으므로 B를 스택에 push 하고, 인접정점 D와 E 중에서 오름차순에 따라 D를 선택하여 탐색을 계속한다.

push(B);
D 방문;
visited[D] <- true;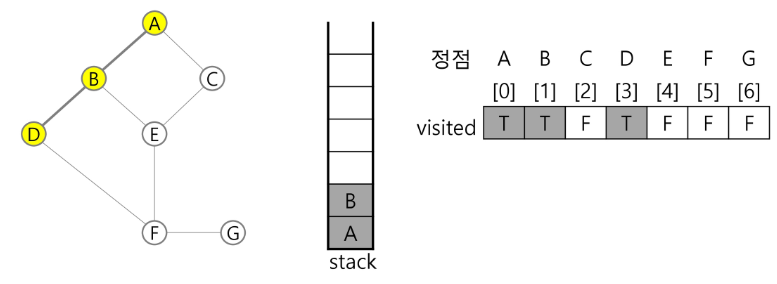

4) 정점 D에 방문하지 않은 정점 F가 있으므로 D를 스택에 push 하고, 인접정점 F를 선택하여 탐색을 계속한다.

push(D);
F 방문;
visited[F] <- true;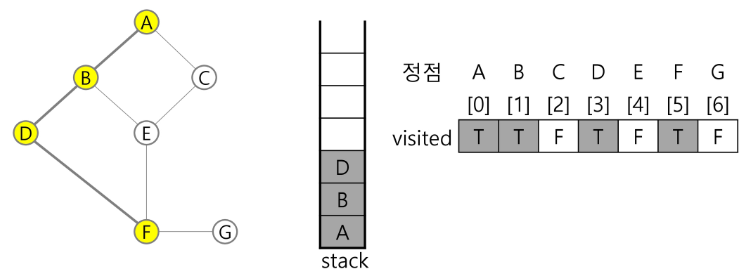

5) 정점 F에 방문하지 않은 정점 E, G가 있으므로 F를 스택에 push 하고, 인접정점 E와 G 중에서 오름차순에 따라 E를 선택하여 탐색을 계속한다

push(F);
E 방문;
visited[F] <- true;

6) 정점 E에 방문하지 않은 정점 C가 있으므로 E를 스택에 push 하고, 인접정점 C를 선택하여 탐색을 계속한다

push(E);
C 방문;
visited[C] <- true;

7) 정점 C에서 방문하지 않은 인접정점 이 없으므로, 마지막 정점으로 돌아가기 위해 스택을 pop 하여 받은 정점 E에 대해서 방문하지 않은 인접정점이 있는지 확인한다.

pop(stack);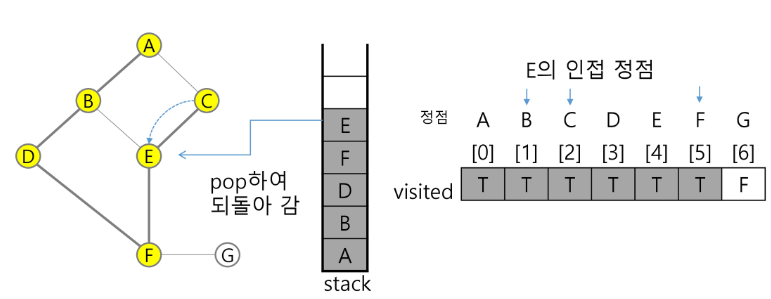

8) 정점 E에서 방문하지 않은 인접정점 이 없으므로, 다시 스택을 pop 하여 받은 정점 F에 대해서 방문하지 않은 인접정점이 있는지 확인한다.

pop(stack);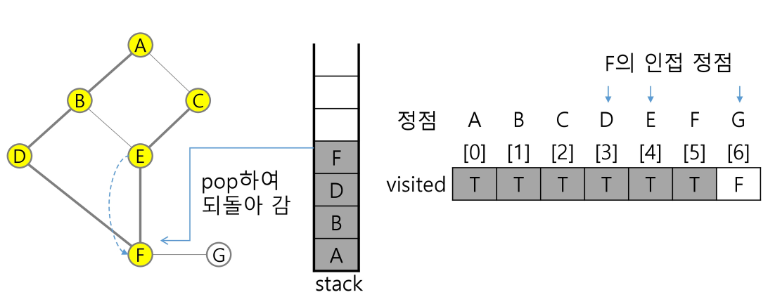

9) 정점 E에 방문하지 않은 정점 G가 있으므로 F를 스택에 push 하고, 인접정점 G를 선택하여 탐색을 계속한다

push(F);
G 방문;
visited[G] <- true;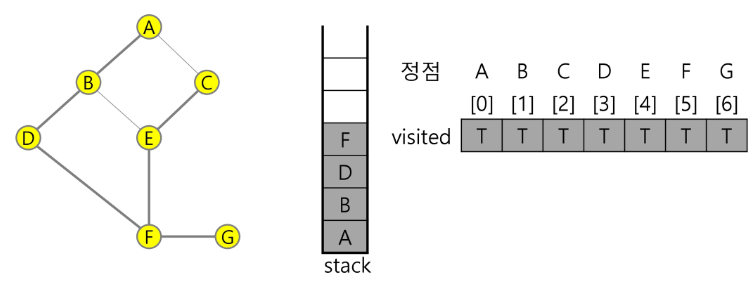

10) 정점 G에서 방문하지 않은 인접정점 이 없으므로, 마지막 정점으로 돌아가기 위해 스택을 pop하여 받은 정점 F에 대해서 방문하지 않은 인접정점이 있는지 확인한다.

pop(stack)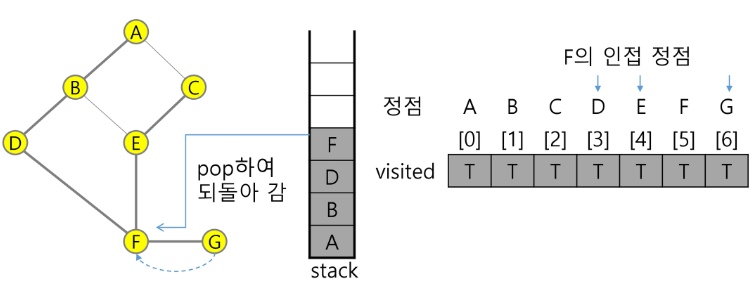

11) 정점 F에서 방문하지 않은 인접정점 이 없으므로, 다시 마지막 정점으로 돌아가기 위해 스택을 pop하여 받은 정점 D에 대해서 방문하지 않은 인접정점이 있는지 확인한다.

pop(stack)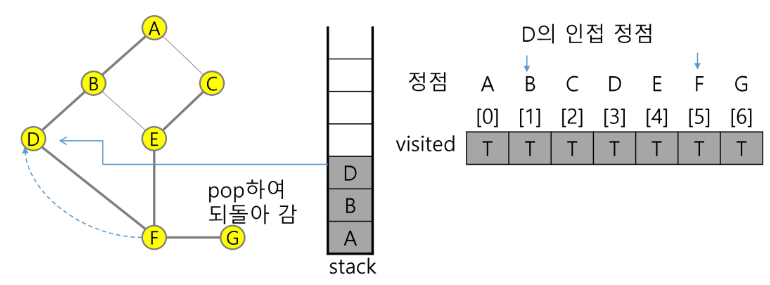

12) 정점 D에서 방문하지 않은 인접정점 이 없으므로, 다시 마지막 정점으로 돌아가기 위해 스택을 pop하여 받은 정점 B에 대해서 방문하지 않은 인접정점이 있는지 확인한다.

pop(stack)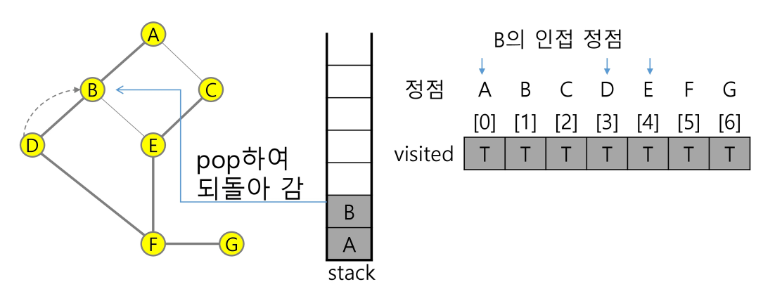

13) 정점 B에서 방문하지 않은 인접정점 이 없으므로, 다시 마지막 정점으로 돌아가기 위해 스택을 pop하여 받은 정점 A에 대해서 방문하지 않은 인접정점이 있는지 확인한다.

pop(stack)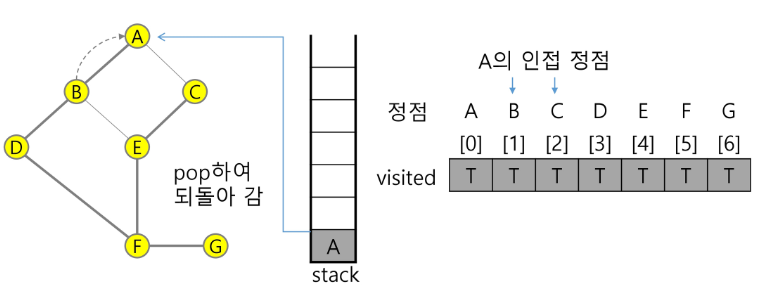

14) 정점 A에서 방문하지 않은 인접정점 이 없으므로, 마지막 정점으로 돌아가기 위해 스택을 pop하는데, 스택이 공백이므로 깊이 우선 탐색을 종료한다.

jun_grammer

게임개발자가 되는 그날까지

이전 포스트

알고리즘 (스택, 재귀, 메모이제이션)

다음 포스트