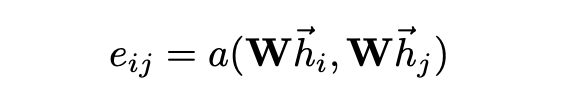
📌 GRAPH ATTENTION NETWORKS

📖 ABSTRACT

본 논문에서 소개하는 Graph Attention Networks (GATs)는 GCN 방법론을 포함한 기존 방법론들의 단점을 극복하기 위해 Masked Self-Attention Layers를 사용한다.

해당 모델은 Inductive 및 Transductive Graph Benchmarks에 해당하는 데이터셋에 대해 SOTA 성능을 달성했음을 보인다.

📖 INTRODUCTION

GCN 두 가지 접근법

1.Spectral approaches
Spectral 접근법을 기반으로한 GCN의 거듭된 발전은 SEMI-SUPERVISED CLASSIFICATION WITH GRAPH CONVOLUTIONAL NETWORKS 해당 논문에 정리되어있다.

저자는 다음의 접근법에 대한 한계로 학습된 필터가 의존하는 Laplacian eigenvector가 그래프 구조에 따라 달라지는 것을 언급한다.
관련 내용은 GCN 논문 리뷰를 참고하면 도움이 될 것이다.

2. Spatial approaches
Spatial 접근법을 기반으로 노드 표현을 계산하기 위한 방법인 GCN 방법론에는 GraphSAGE가 있으며, 저자는 다음 모델이 대규모 Inductive benchmarks에서 인상적인 성능을 얻었음을 언급한다.
GraphSAGE 논문 리뷰를 참고하면 이해하는 데 도움이 될 것이다.

Self-Attention

본 논문에서 저자는 Self-Attention이 RNN 또는 CNN을 기반으로 한 방법론을 개선했을 뿐만 아니라 기계 번역 작업에서 SOTA 성능을 달성하다는 데 충분하다고 주장한 논문 Attention Is All You Need에 영감을 받아 노드 분류를 수행하기 위해 Attention을 기반으로 아키텍처를 구성하여 제안한다.

📖 BACKGROUND

다음 Attention Mechanism 소개 섹션은 이해하는 데 많은 도움을 받은 딥 러닝을 이용한 자연어 처리 입문 중 15-01 어텐션 메커니즘 (Attention Mechanism)의 구성을 그대로 가져와서 설명함을 밝힙니다.

seq2seq 모델

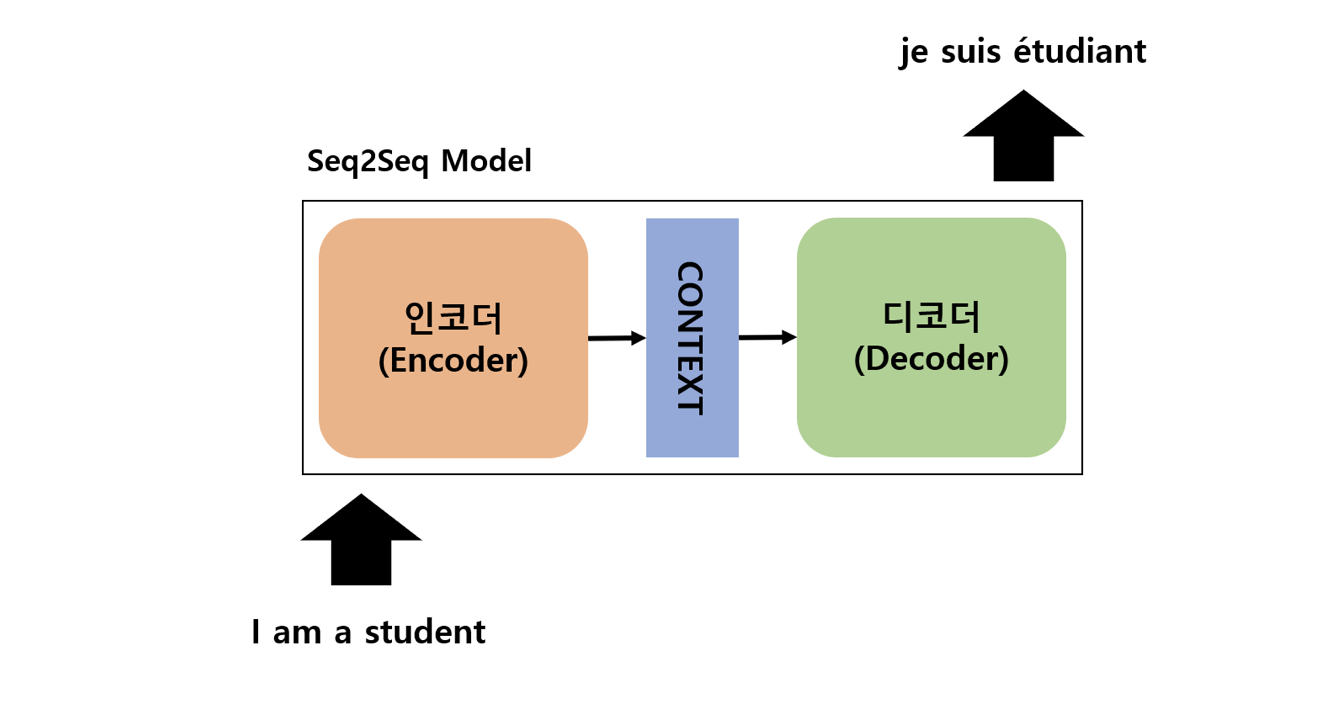
Seq2Seq 구성

Seq2Seq 모델은 위의 그림과 같이 인코더와 디코더로 구성되어 있다.

인코더는 입력 시퀀스를 받아 하나의 고정된 크기인 벡터 표현으로 압축한다.
압축된 벡터 표현은 컨텍스트 벡터라 부른다.
디코더는 압축된 컨텍스트 벡터를 전달 받아 이를 통해 출력 시퀀스를 만들어낸다.

Seq2Seq 한계점

RNN에 기반한 seq2seq 모델은 두 가지의 한계점을 갖고있다.

1. 하나의 고정된 크기인 컨텍스트 벡터에 입력 시퀀스의 모든 정보를 압축하려다 보니 정보 손실이 발생한다.
2. RNN의 고질적인 문제인 기울기 소실 문제가 존재한다.

Attention Mechanism

Attention의 아이디어

어텐션의 기본 아이디어는 디코더가 각 출력 단어를 생성할 때, 인코더의 모든 입력 단어에 주의를 기울이는 대신 해당 시점에 예측해야 할 단어와 연관이 있는 입력 단어에 좀 더 주의를 기울이도록 하는 것이다.

Attention 함수

Attention 함수는 Query, Key, Value로 구성된다.
Seq2Seq 모델에서 어텐션 모델의 Query, Key, Value는 각각 다음과 같이 정의한다.

Q = Query : t 시점의 디코더 셀에서의 은닉 상태
K = Keys : 모든 시점의 인코더 셀의 은닉 상태들
V = Values : 모든 시점의 인코더 셀의 은닉 상태들

Attention Mechanism 과정

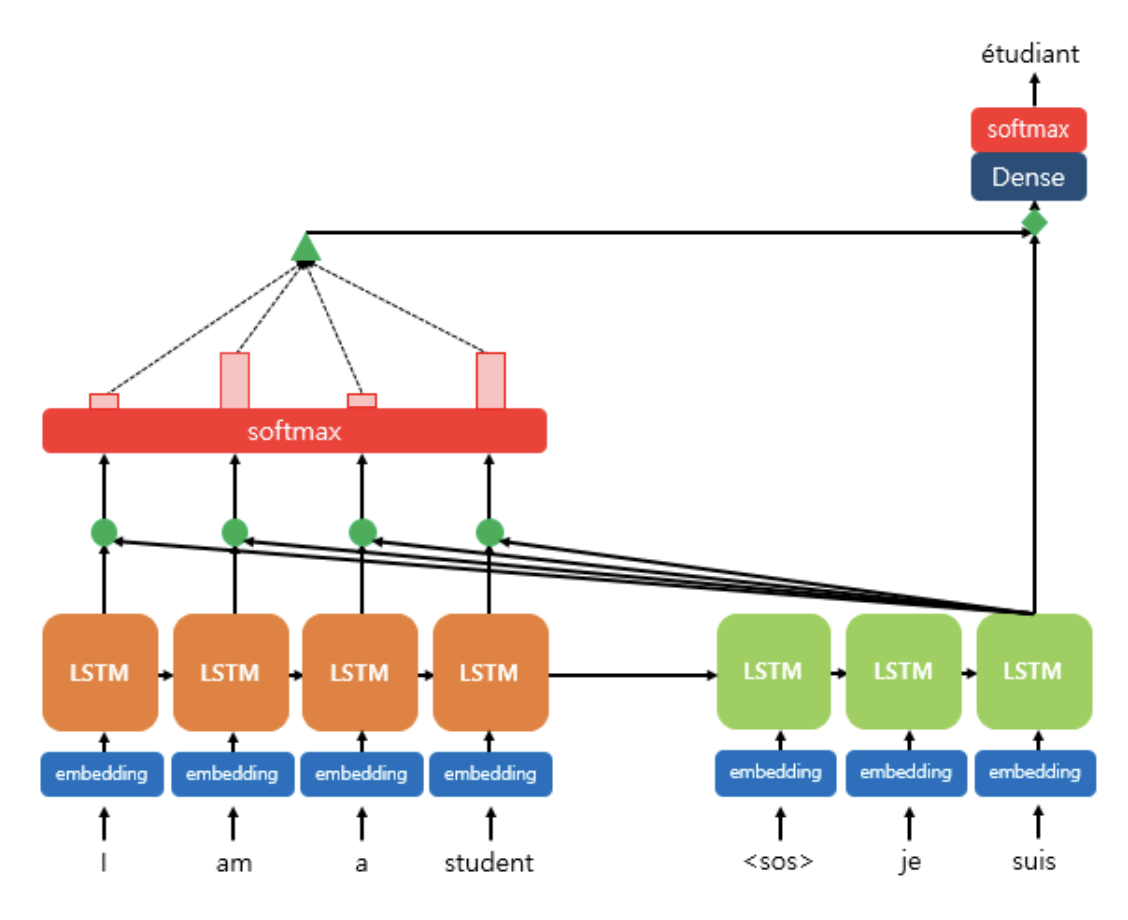
위의 어텐션 과정은 디코더가 3번째 출력 단어를 예측할 때, 어텐션 메커니즘을 사용하는 모습을 보인다.
디코더의 3번째 LSTM 셀은 출력 단어를 예측하기 위해서 인코더의 모든 입력 단어들의 정보를 다시 한번 참고한다.

좀 더 구체적인 과정을 살펴보자.

1. 어텐션 스코어(Attention Score)를 구한다.

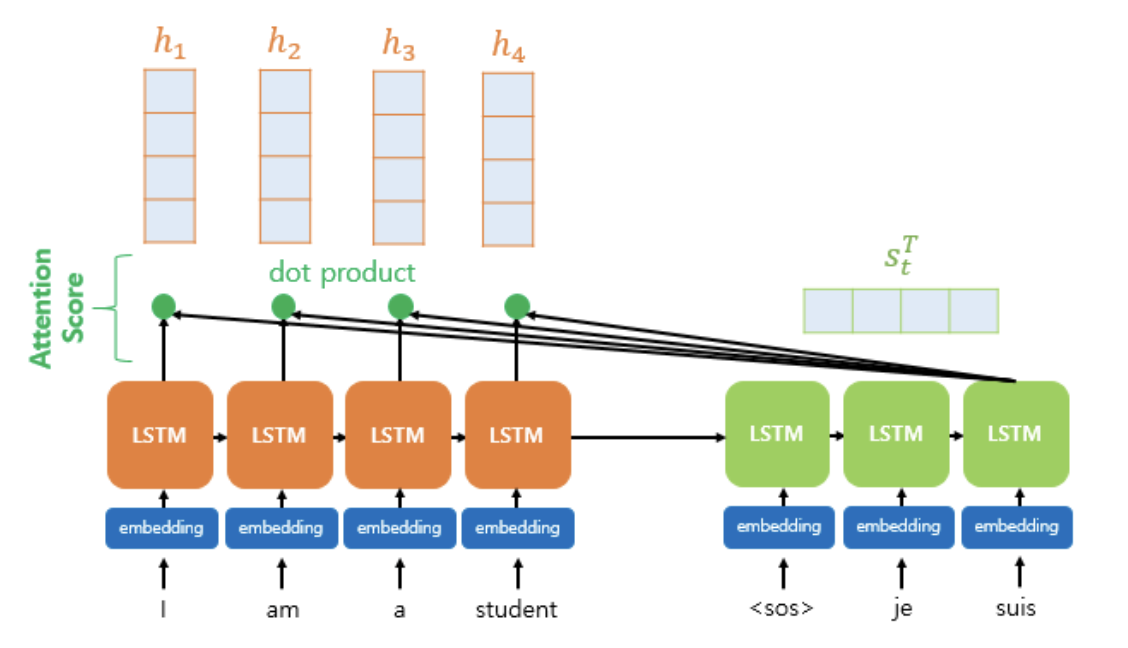
인코더의 은닉 상태를 각각 $h_1, h_2, ...\,, h_N$이라고 한다.
현재 시점 t에서 디코더의 은닉 상태를 $s_t$라고 한다.
추가로 인코더의 은닉 상태와 디코더의 은닉 상태가 동일하게 차원이 4라고 가정한다.

어텐션 메커니즘에서 디코더의 필요한 입력값은 이전 시점인 $t-1$의 은닉 상태와 이전 시점 $t-1$에 나온 출력 단어, 추가로 어텐션 값 $a_t$이다.

어텐션 스코어 $a_t$는 현재 디코더의 시점 $t$에서 단어를 예측하기 위해, 인코더의 모든 은닉 상태 $h$ 각각이 디코더의 현 시점 은닉 상태 $s_t$와 얼마나 유사한지를 판단하는 스코어값이다.

예를 들어, 위 그림에서 디코더의 현 시점 은닉 상태를 왼쪽 열에 있는 단어 it이라 하고, 오른쪽 열에 각각의 단어들을 인코더의 모든 은닉 상태라 생각하면 쉽다.
다음 10개의 단어에 대해 it이 얼마나 유사한지에 따라 어텐션 스코어 값이 나오게 된다.

위의 영어 문장을 읽었을 때 단어 it은 원숭이를 의미한다고 보여지기 때문에 인코더에 위치한 은닉 상태 monky에 대해 가장 높은 어텐션 스코어 값이 부여될 것이다.

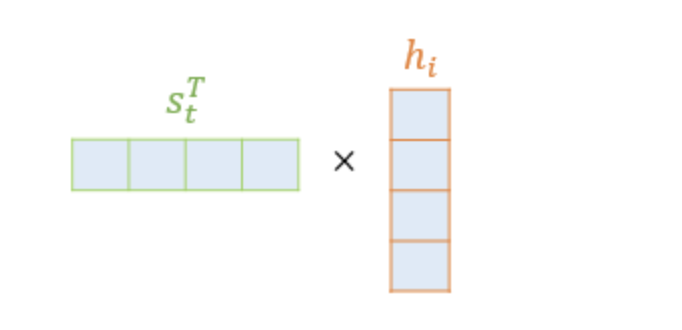
어텐션 스코어를 구하는 함수 중 하나인 닷-프로덕트 어텐션에서는 위 그림과 같이 스코어 값을 구하기 위해 $s_t$를 전치하고 각 은닉 상태와 내적을 수행한다.
이에 따라 모든 어텐션 스코어 값은 스칼라이다.

추가로 $s_t$와 인코더의 모든 은닉 상태의 어텐션 스코어의 모음값을 $e^t$라고 정의한다.
$e^t = [s^T_th_1, ...\, ,s^T_th_N]$

2. 소프트맥스 함수를 통해 어텐션 분포를 구한다.

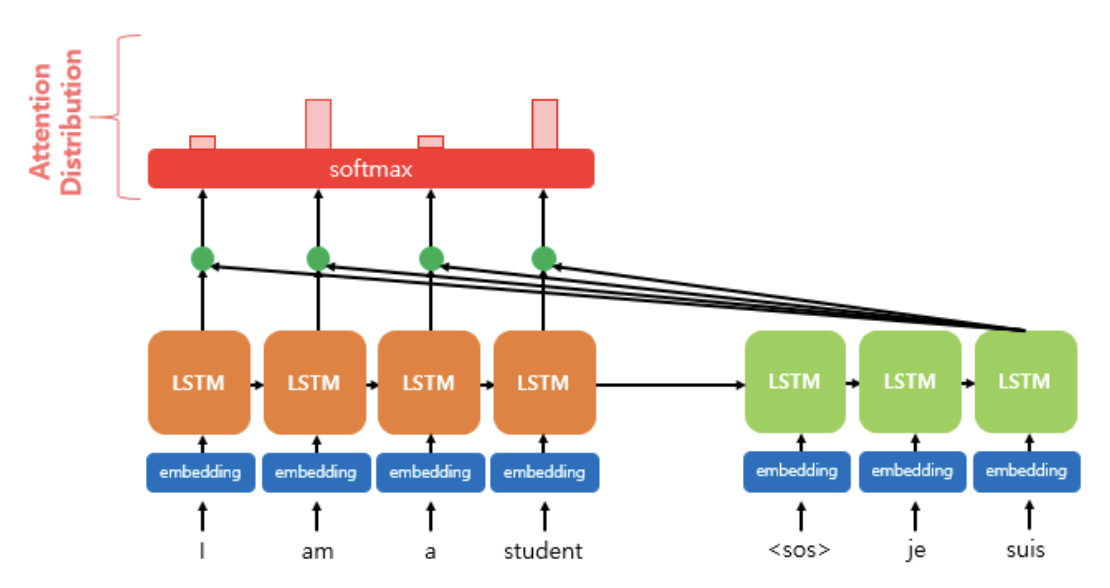
$e^t$에 소프트맥스 함수를 적용하여 모든 값을 합하면 1이 되는 확률 분포를 얻어낸다.
이를 통해 각 은닉 상태에 대한 어텐션 가중치를 만든다.
위 그림에서 softmax 상자 위에 위치한 4개의 막대 그래프는 각각의 은닉상태에 대한 어텐션 가중치를 의미한다.

예를 들어 위에서 예시로 들었던 문장 "The monkey ate that banana because it was too hungry"는 디코더의 은닉 상태 it에 대해 각각의 어텐션 가중치로 $[0.3, 0.4, 0.02, 0.05, 0.1, 0.02, 0.05, 0.02, 0.02, 0.02]$ 값을 갖게 될 것이다.
The와 monky는 it과 비슷한 의미를 가진다는 이유로 나머지 단어들과 비교했을 때 높은 어텐션 가중치를 갖게 됨을 알 수 있으며, 이들의 총합은 $1$이다.

디코더의 시점 t에서의 어텐션 가중치의 모음값인 어텐션 분포를 $α^t$이라고 할 때, 식으로 정의하면 다음과 같다.
$α^t = softmax(e^t)$

3. 각 인코더의 어텐션 가중치와 은닉 상태를 가중합하여 어텐션 값을 구한다.

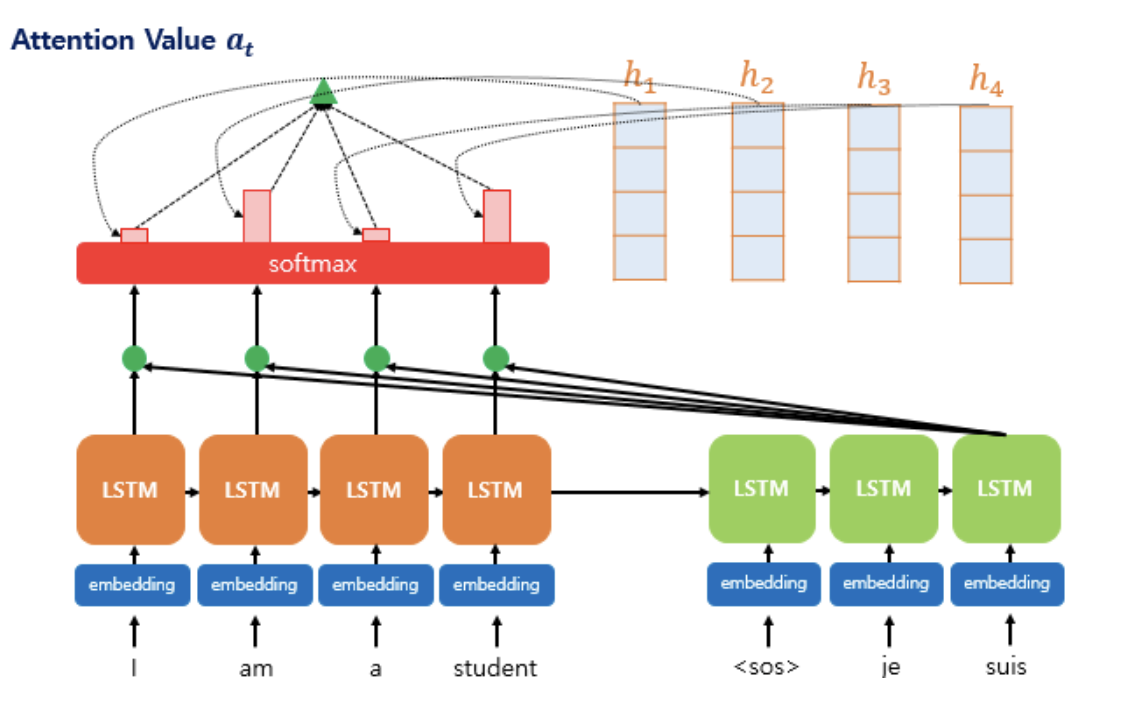
어텐션의 최종 결과값을 얻기 위해서 각 인코더의 은닉 상태와 어텐션 가중치값들을 곱하고, 최종적으로 모두 더한다.
즉 가중합을 진행하게 된다.
어텐션 함수의 출력값인 어텐션 값 $a^t$에 대한 식은 다음과 같다.
$a^t = ∑^N_{i=1}a^t_ih_i$

4. 어텐션 값과 디코더의 $t$ 시점의 은닉 상태를 연결한다.

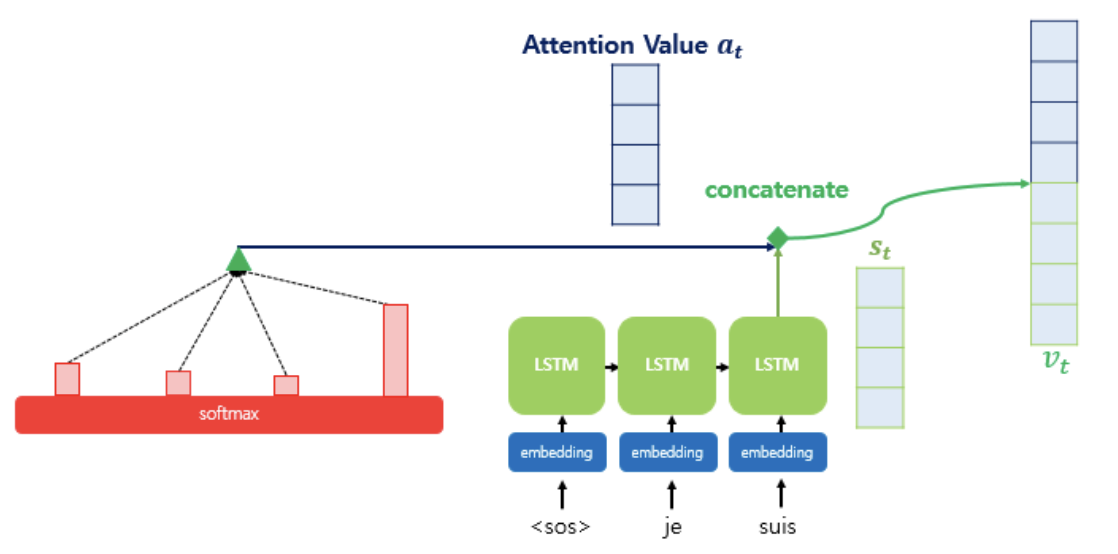
어텐션 메커니즘을 모두 거쳐 얻은 어텐션 값 $a^t$를 디코더의 $t$시점 은닉 상태 $s_t$와 결합하여 하나의 벡터 $v_t$로 만든다.

5. 출력층 연산의 입력이 되는 $ŝ$를 계산한다.

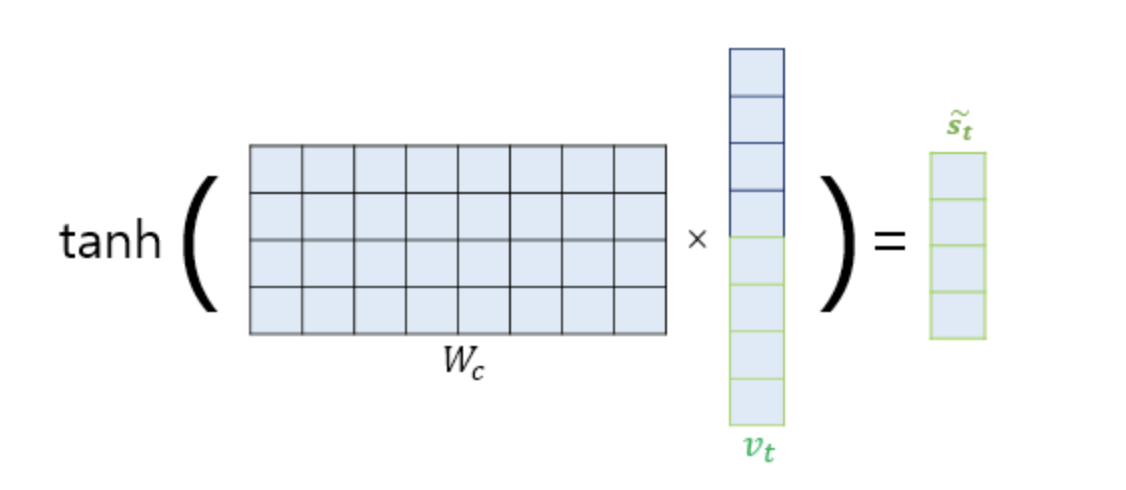
$v_t$를 바로 출력층으로 보내기 전에 신경망 연산을 한 번 더 진행한다.
가중치 행렬과 곱한 후 하이퍼볼릭탄젠트 함수를 지나도록 하여 출력층 연산을 위한 새로운 벡터인 $ŝ$를 얻는다.

$ŝ = tanh(W_c[a_t;s_t] + b)$

6. $ŝ$를 출력층의 입력으로 사용한다.
마지막으로 $ŝ$를 출력층의 입력으로 사용하여 예측 벡터를 얻는다.

$ŷ_t = Softmax(W_yŝ_t + b_y)$

앞서 진행한 attention mechanism 일련의 과정이 GAT 모델에서 활용된다.

📖 GAT ARCHITECTURE

GRAPH ATTENTIONAL LAYER

1. input & output

$Denote$
$input$ : 노드 특징들의 집합, $h =$ {$h_1, h_2, \, ...\, h_N$ }$, \,h_i ∈ ℝ^F$
$output$ : 새로운 노드 특징들의 집합 $h' =$ {$h'_1, h'_2, \, ...\, h'_N$ }$, \,h'_i ∈ ℝ^{F'}$
$N$ : 노드의 수
$F$ : 각 노드의 특징수

2. attention coefficients

$Denote$
$e_{ij}$ : 대상 노드 $i$에 대한 노드 $j$의 중요성을 나타내는 attention coefficients
$a$ : attention mechanism
$W ∈ ℝ^{F' × F}$ : 모든 노드에 적용되는 가중치 매트릭스
$j ∈ N_i$ : 노드 $i$의 1차 이웃 집합

1. 입력 특성 $h$를 고수준의 특성으로 변환하기 위해 학습 가능한 가중치 행렬 $W$로 선형 변환한다.
2. $i$의 1차 이웃 노드 집합 $j$를 대상으로 self-attention을 수행하여 각 노드들에 대한 attention coefficients $e_{ij}$를 계산한다.

위 self-attention 과정에서는 대상 노드의 특성과 대상 노드의 1차 이웃 노드의 특성의 연관성을 기반으로 가중치를 도출한다.

3. softmax function

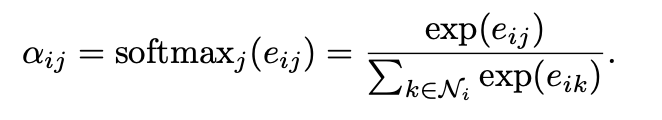
해당 수식은 타겟 노드 $i$에 대해 가능한 모든 노드 $j$의 attention coefficients를 소프트맥스 함수를 사용하여 정규화하는 것을 나타낸다.

4. attention mechanism

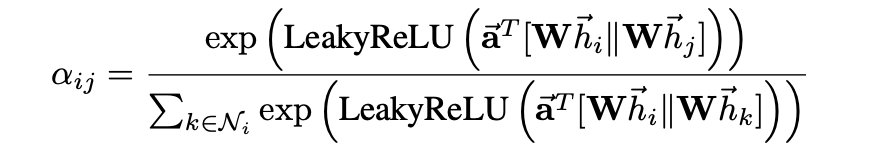
$∣∣$는 concatenation 연산을 의미한다.

본 논문의 실험에서 attention mechanism은 가중치 벡터 $a ∈ R^{2F'}$를 매개변수로 갖으며, LeakyReLU 비선형성을 사용한 단일 레이어의 피드 포워드 신경망이다.

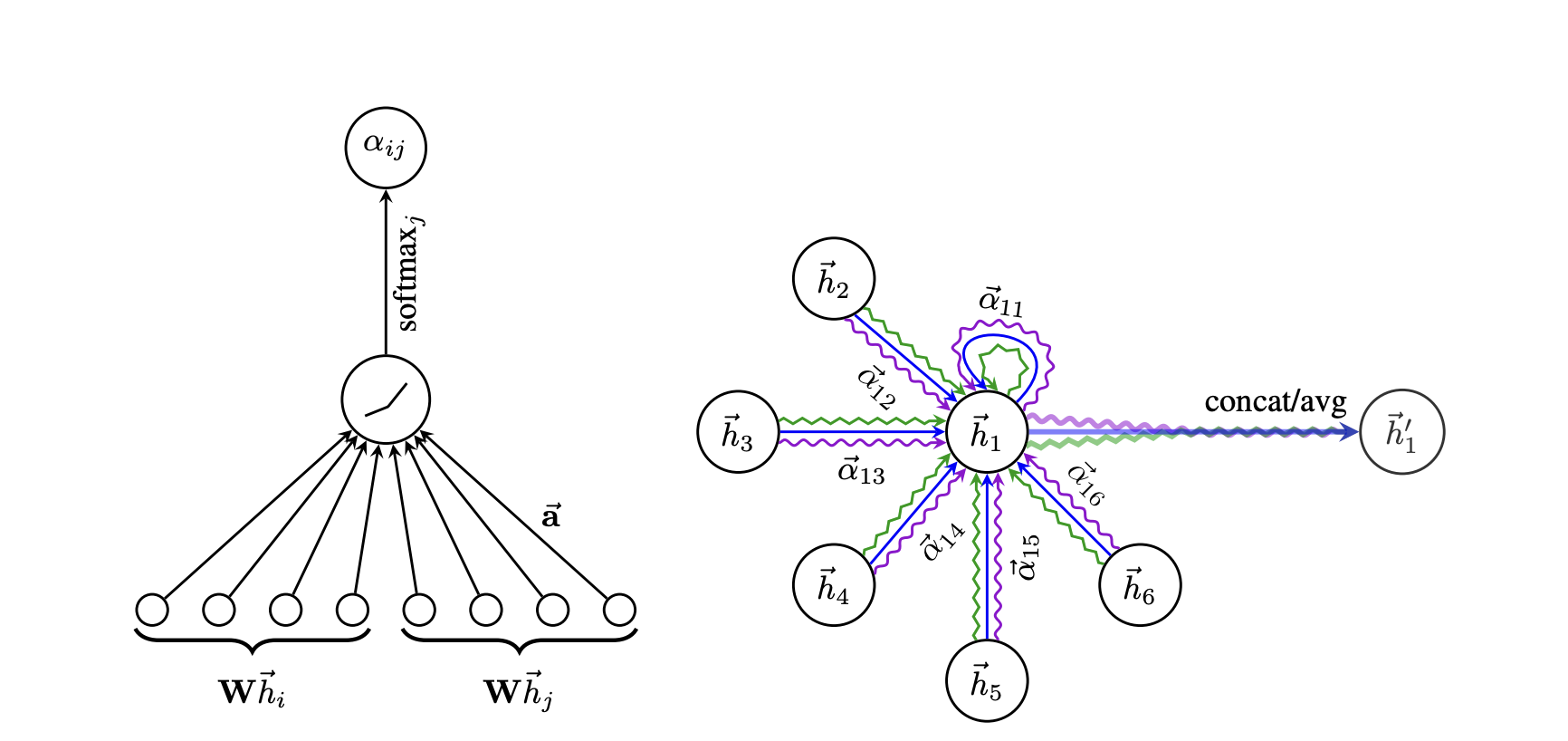
여기까지의 과정을 그림으로 표현하면 다음과 같다.

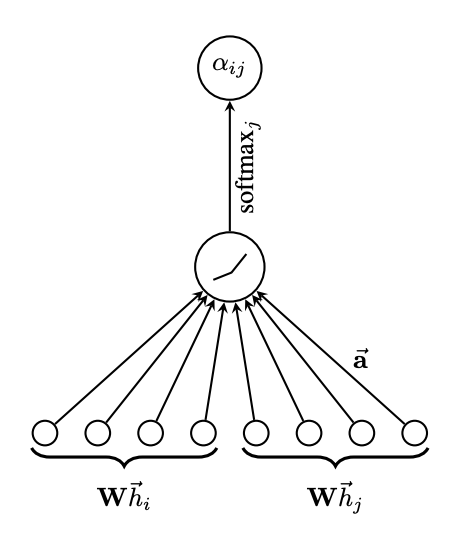
5. aggregated features

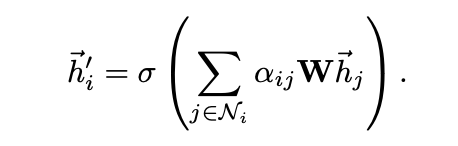
정규화된 attention coefficients를 얻은 후 각 노드의 최종 출력은 해당 노드의 이웃들과의 특성의 가중합으로 표현되며, 이에 비선형 함수가 적용될 수 있다.

6. multi-head attention

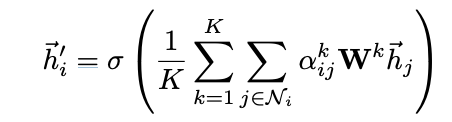
self-attention의 학습과정을 안정화하기 위해 multi-head attention을 사용한다.

$K$개의 독립적인 attention mechanism이 위 aggregated features에서 보인 수식으로 수행된 후 그 결과로 얻은 특성들의 평균을 사용한다.
즉, 여러 attention head의 출력을 평균으로 계산하여 각 노드의 최종 출력을 얻는다.

다음 과정을 그림으로 표현하면 다음과 같다.

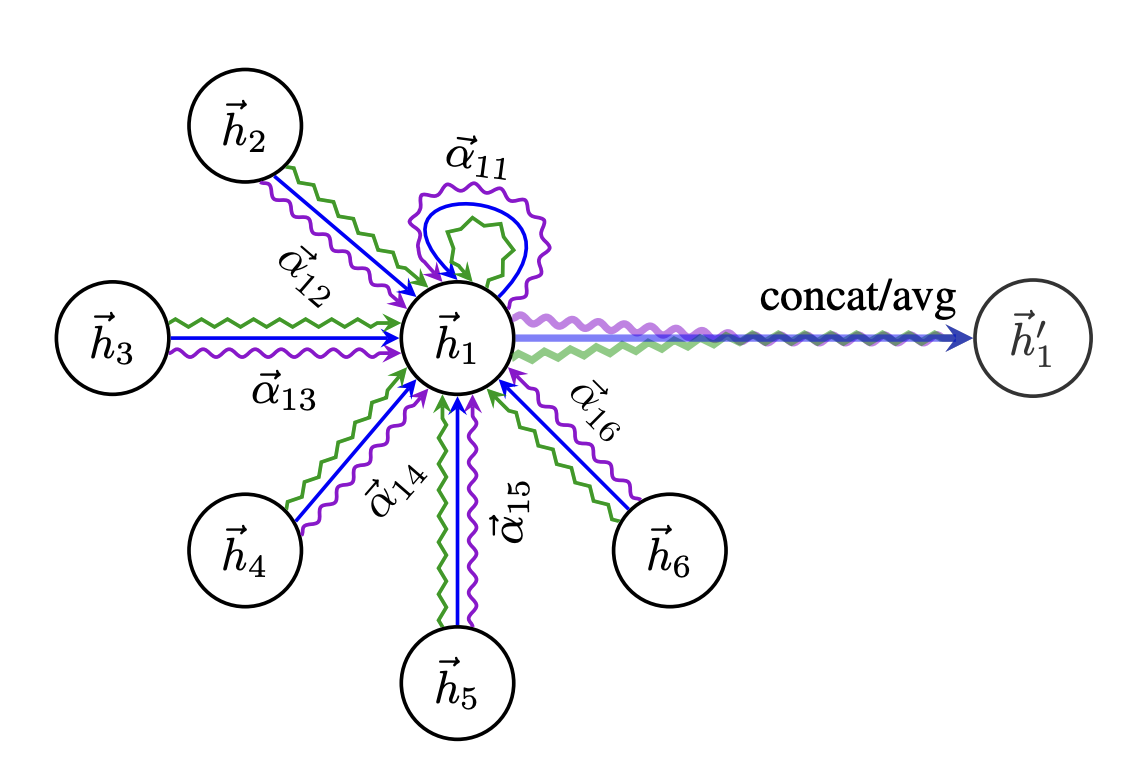
COMPARISONS TO RELATED WORK

garph attention layer는 신경망을 사용한 그래프 구조 데이터의 모델링에 대한 이전 접근 방식에서 나타난 여러 문제점을 개선한다.

1. 계산의 효율화 : self-attention 레이어의 작업은 모든 엣지에 대해 병렬로 수행될 수 있으며, 출력 특성의 계산은 모든 노드에 대해 병렬로 수행될 수 있다.
   따라서 eigendecompositions나 유사한 행렬 연산 방식처럼 비용이 많이 들지 않는다.
2. GCN과 달리 GAN은 노드에 대해 다른 중요도를 지정할 수 있으며, 이는 해석 가능성에 이점을 제공할 수 있다.
3. 전체 그래프 구조를 사전에 알 필요가 없어 이전 스펙트럼 기반 접근 방식의 이론적 문제를 해결한다.

📖 EVALUATION

모델의 실험은 inductive task와 transductive task 모두에서 진행했으며, 두 데이터셋 모두에서 GAT는 가장 좋은 성능을 보인다.

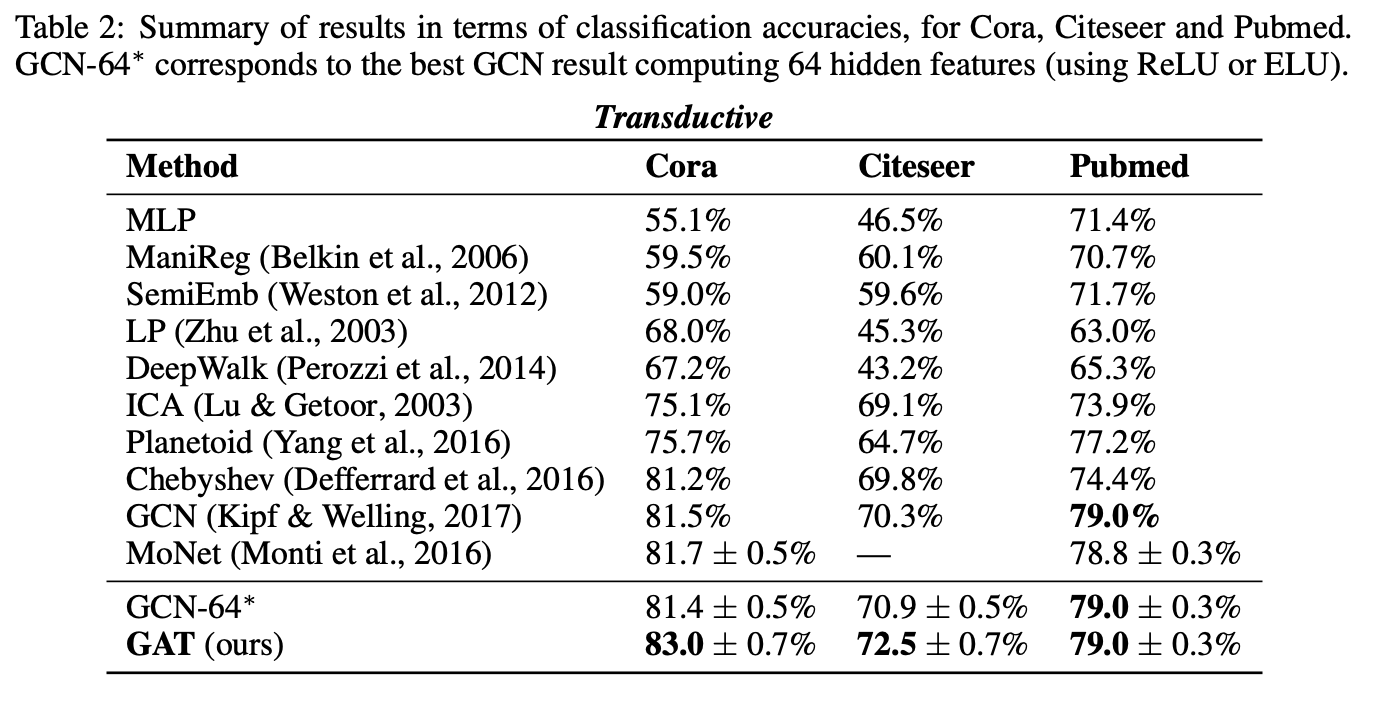
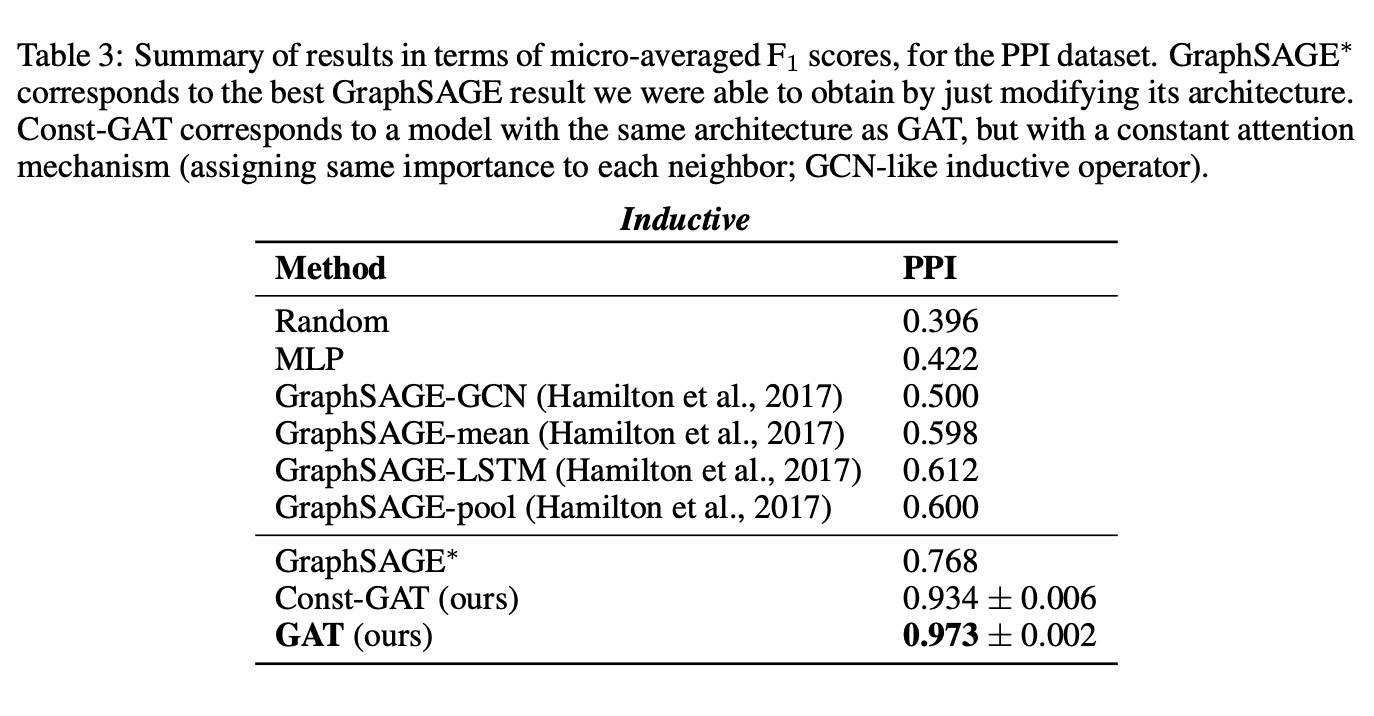
위 그림은 t-SNE로 시각화된 GAT 모델의 특성 표현은 데이터셋의 레이블에 따라 구별 가능한 클러스터를 보여주며, 모델이 데이터를 효과적으로 분류함을 보인다.

📖CONCLUSIONS

GAT는 각 노드 특성의 연관성을 기반으로 가중치를 부여한다는 점에서 의미적으로 합당한 가중치 부여방식이라고 생각했으며, 해당 논문을 공부하며 attention mechanism에 대해 다시 한번 공부할 수 있는 계기가 되었다.

Reference

GRAPH ATTENTION NETWORKS
[DMQA Open Seminar] Graph Attention Networks
딥 러닝을 이용한 자연어 처리 입문 : 15-01 어텐션 메커니즘 (Attention Mechanism)