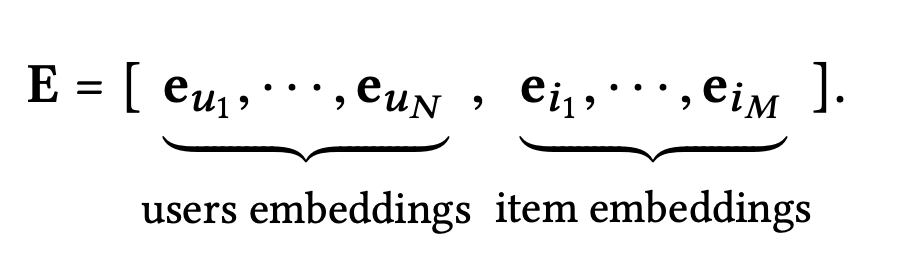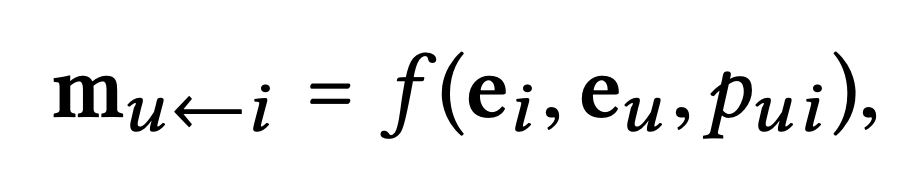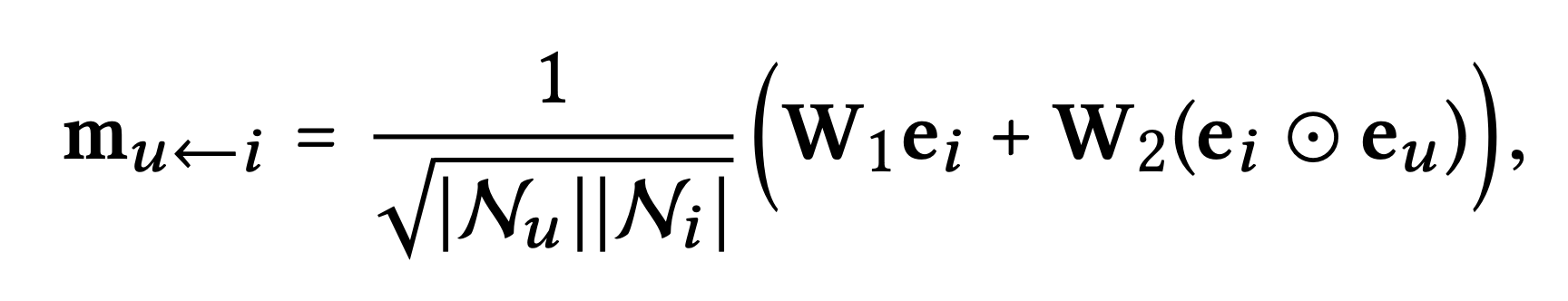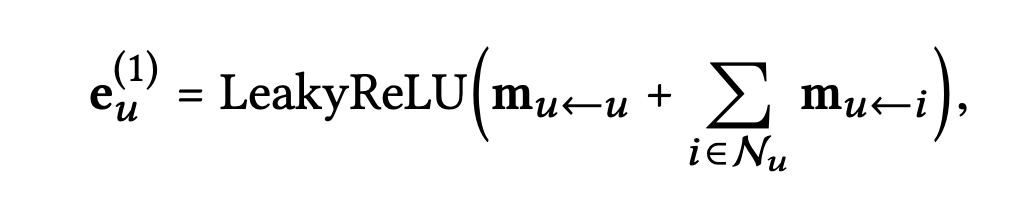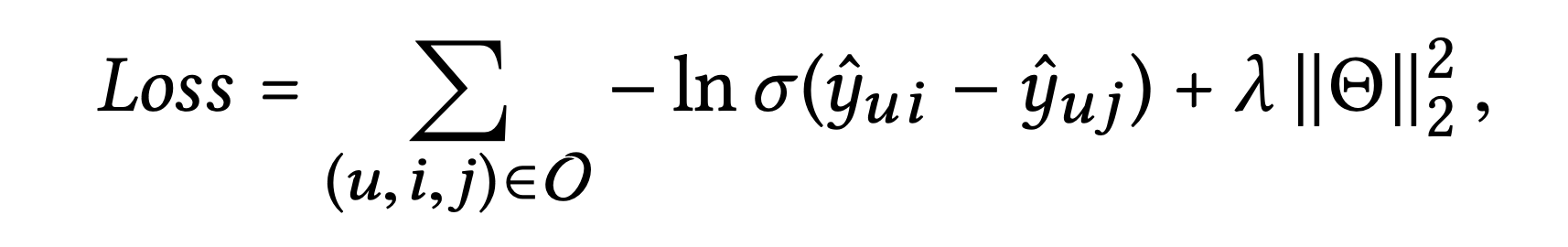
📌 Neural Graph Collaborative Filtering
📖 Abstract
- 기존의 방법들은 임베딩 과정에서 사용자-아이템 상호 작용에서의 잠재적인 협력 신호를 인코딩하지 못한다는 한계점을 언급한다.
- 저자는 사용자-아이템 그래프 구조를 활용하여 임베딩을 전파 할 것을 제안하며, 이를 Neural Graph Collaborative Filtering이라고 명명한다.
- 결과적으로 사용자-아이템 그래프의 고차 연결성을 효과적으로 모델링하며, 임베딩 과정에 협력 신호를 주입함으로써 협력 필터링 효과를 향상시킨다.
📖 Introduction
학습 가능한 협력 필터링 모델의 주요 구성 요소는 다음의 두 가지가 있다.
- 임베딩 (Embedding) : 사용자와 항목을 벡터화된 표현으로 변환하는 구성 요소
- 상호 작용 모델링 (Interaction Modeling) : 임베딩을 기반으로 과거 상호작용을 재구성하는 구성 요소
기존의 방법들은 임베딩 함수에 사용자-아이템 상호 작용에서 나타나는 협력 신호를 명시적으로 인코딩하지 않기 때문에 협력 신호를 위한 만족스러운 임베딩을 생성하기에 충분하지 않다.
결과적으로 이러한 방법들은 임베딩이 협력 신호를 충분히 포착하지 못할 때, 부적절한 임베딩의 결함을 보완하기 위해 상호 작용 함수에 의존하게 된다.
이를 해결하기 위해 본 연구에서는 사용자-아이템 상호 작용에서 고차 연결성을 활용하며, 이는 협력 신호를 상호 작용 그래프 구조에 인코딩하는 방법이다.
정리하면 지금까지의 연구들이 위의 두 가지 구성 요소 중 상호 작용 모델링에 집중했다면, 본 연구에서는 임베딩 과정에 협력 신호를 인코딩하기 위한 노력이라고 보여진다.
High-order connectivity
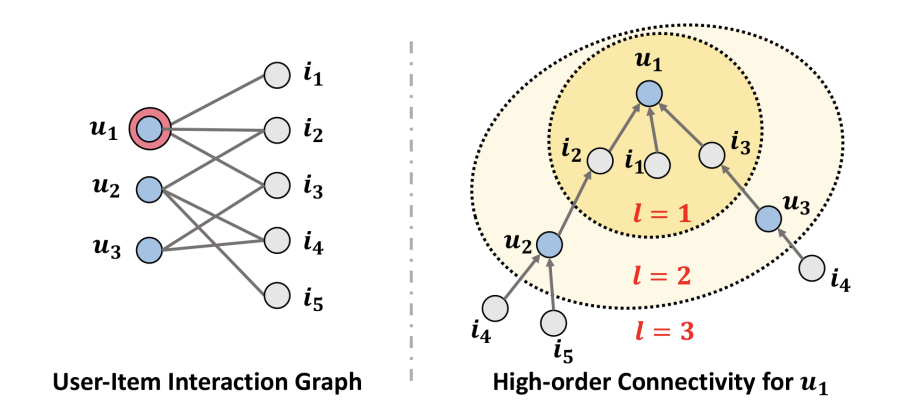
오른쪽의 그림은 왼쪽의 사용자-아이템 상호작용 그래프를 기반으로 사용자 의 고차 연결성을 표현한 것이다.
고차 연결성은 User-Item Interaction Graph를 기반으로 하기 때문에 노드의 연결 순서는 user-item-user-item을 반복한다.
해당 고차 연결성의 표현은 각 사용자 혹은 아이템마다 다르게 구성된다.
이러한 고차 연결성은 협력 신호를 나타내는 두가지 의미를 포함한다.
- 오른쪽 그림의 경로 는 사용자 와 모두 아이템 와 상호 작용했기 때문에 사용자 와 의 행동 유사성을 나타내고 유사한 사용자 가 아이템 를 채택했기 때문에 사용자 또한 아이템 를 채택할 가능성이 높을 수 있음을 의미한다.
- 오른쪽 그림 범위에서 아이템 와 사용자 을 연결하는 경로가 두개인 반면, 아이템 와 사용자 을 연결하는 경로는 한 개이기 때문에 이는 아이템 가 아이템 보다 사용자 의 관심을 끌 가능성이 높다는 것을 의미한다.
해당 연구에서는 임베딩 함수 내에서 고차원 연결성 정보를 모델링하는 방법을 제안한다.
Contribution
- 모델 기반 CF 방법의 임베딩 함수에서 협업 신호를 명시적으로 활용하는 것의 중요성을 강조한다.
- 저자는 임베딩 전파를 통해 고차원 연결성 형태로 협업 신호를 명시적으로 인코딩하는 그래프 신경망을 기반으로 한 새로운 추천 프레임워크 NGCF를 제안한다.
- 저자는 실험을 통해 NGCF의 최첨단 성능과 품질 향상에 대한 신경망 임베딩 전파의 효과를 입증한다.
📖 METHODOLOGY
1. Embedding Layer
: user (item ) with an embedding vector
: embedding size
임베딩 레이어는 모델의 입력 데이터를 연속적인 벡터로 변환하는 역할을 한다.
사용자와 아이템을 고차원 벡터 공간에 매핑하여 사용자 및 아이템의 특징 및 상호작용을 표현하는 데 사용된다.
기존의 방법들은 이러한 임베딩을 직접 상호 작용 레이어로 공급하여 예측 점수를 얻는 반면 NGCF는 초기 임베딩을 사용자와 아이템 간의 상호작용 그래프를 통해 개선하고, 이를 통해 추천 작업에 더 적합한 임베딩을 얻을 수 있다.
즉, 임베딩을 개선하는 단계를 추가하여 모델이 더 나은 품질의 임베딩을 학습하도록 돕는다는 점에서 기존 모델과 차이가 있다.
2. Embedding Propagation Layers
임베딩 전파 레이어는 그래프 신경망(GNN)의 메시지 전달 아키텍처를 기반으로,
그래프 구조를 따라 협력 신호를 캡처하고 사용자 및 아이템의 임베딩을 개선한다.
먼저 한 층의 전파 설계를 설명하고, 이를 기반으로 여러 연속적인 층에 일반화한다.
First-order Propagation
연결된 사용자와 아이템 간에 임베딩 전파는 메시지를 구성하는 단계와 구성된 메시지들을 집계하는 두가지 주요 과정으로 구성되어 있다.
1. Message Construction
연결된 사용자-아이템 쌍에 대해 에서 로의 메세지를 다음과 같이 정의한다
: 메시지 임베딩
: 메시지 인코딩 함수
: 가중 계수(각 전파 경로에서의 감쇠 요인 제어)
는 다음과 같이 구현한다
: 가중치 행렬
: 원소별 곱 (와 간의 상호작용에 의존)
저자는 graph convolution network를 따라 를 그래프 라플라시안 정규화로 설정한다.
는 사용자의 이웃 수를 의미하고, 는 아이템의 이웃 수를 의미한다.
즉, high-order connectivity의 경로 의 길이가 늘어남에따라 이웃의 수는 증가할 것이고 그래프 라플라시안 정규화를 통해 가중치가 감쇠한다.
이로써 는 경로 길이에 따라 메시지를 감소하게 만드는 할인 요소로 해석될 수 있다.
결과적으로 메시지 임베딩 는 의 정보가 담긴 임베딩과 그리고 의 이웃 사용자들 가 상호 작용한 정보가 담긴 임베딩 두개의 합 그것에 할인 요소가 더해진 값을 의미한다.
2. Message Aggregation
이 단계에서는 사용자 의 이웃으로부터 전파된 메시지를 집계하여 사용자 의 표현을 개선한다.
집계 함수는 다음과 같이 정의한다
: 첫 번째 임베딩 전파 층 이후에 얻은 사용자 의 표현
정리하면 임베딩 전파 층은 사용자와 아이템의 표현을 관련시키기 위해 1차 연결성 정보(first-order connectivity)를 명시적으로 활용하는 것이다.
다음은 이러한 과정을 개의 고차 연결성으로 확장한다.
High-order Propagation
개의 임베딩 전파 층을 쌓음으로써 사용자 및 아이템은 -hop이웃에서 전파된 메시지를 받을 수 있다.
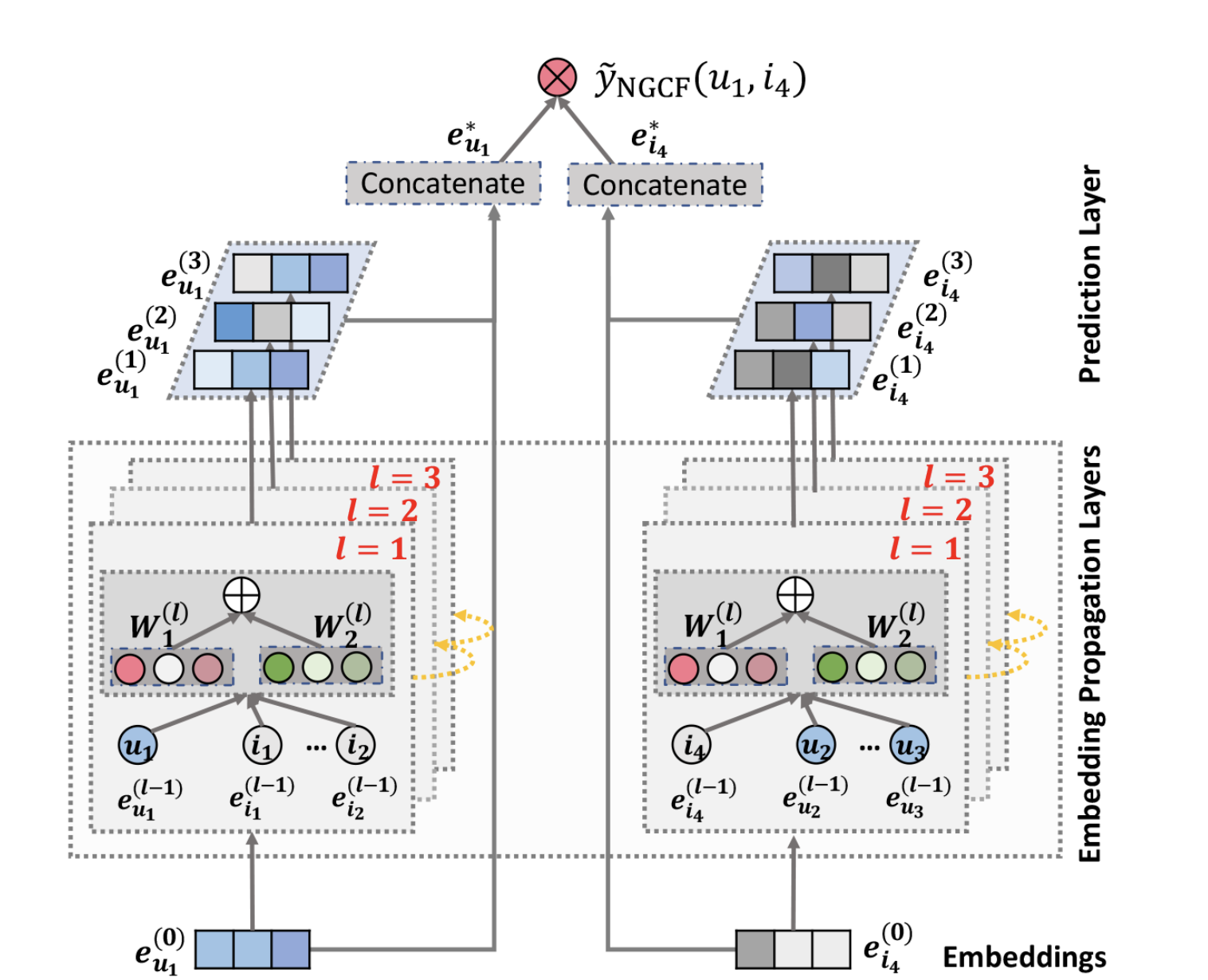
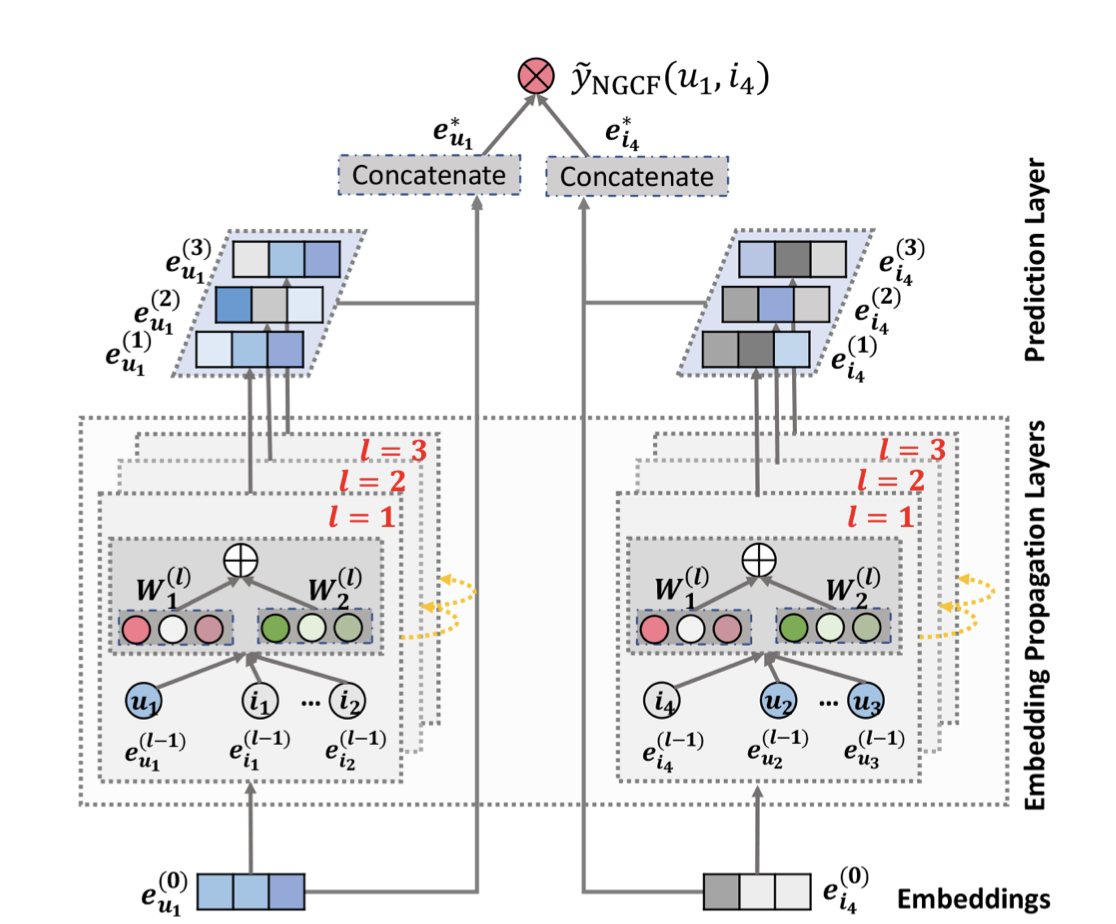
위 그림에서처럼 -번째 단계에서 사용자 의 표현은 다음과 같이 재귀적으로 정의된다.
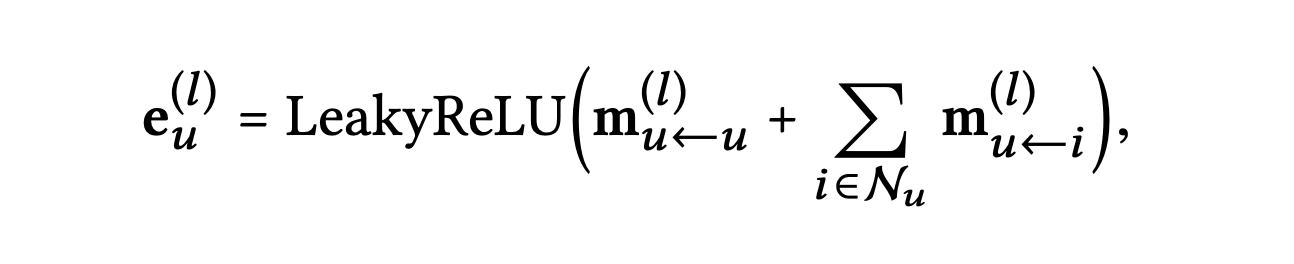
여기서 전파되는 메시지는 다음과 같이 정의된다.

는 이전 메시지 전달 단계에서 생성된 아이템 표현으로 -hop으로부터의 메시지를 의미한다.
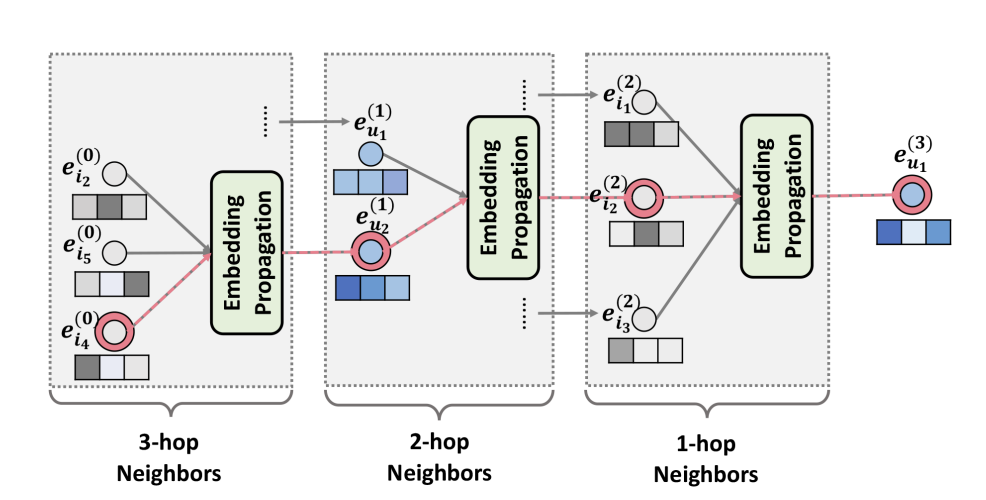
다음의 그림에서 볼 수 있듯이 와 같은 협력 신호는 임베딩 전파 과정에서 포착될 수 있다.
더 나아가 에서의 메시지는 에 명시적으로 인코딩되며, 이것은 여러개의 임베딩 전파 층을 쌓는 것으로 협력 신호를 효과적으로 표현 학습 과정에 주입한다.
Propagation Rul in Matrix Form
위의 Embedding Layer에서 언급했듯이 임베딩 전파를 행렬 형태로 제시함으로써 일괄처리를 용이하게 한다.
다음의 식은 위의 방정식들과 동등한 층별 전파 규칙의 행렬 형태이다.
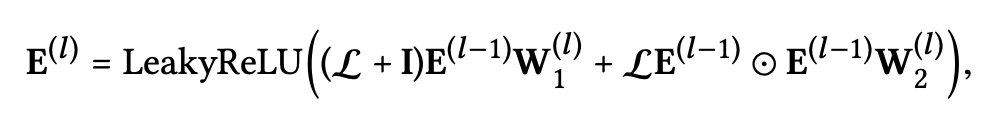
𝓛은 라플라시안 행렬로 다음과 같이 정의된다.
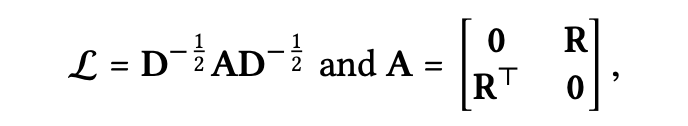
는 인접 행렬이며, 는 대각성분 행렬이다.
의 번째 대각성분 값 이며,
𝓛의 대각성분 외의 0이 아닌 항은 값을 갖는다.
이는 위에서 할인 요소로 해석되었던 의 값과 같다.
라플라시안 행렬에 대한 설명은 GCN 논문 리뷰에 정리되어있다.
결과적으로 행렬 형태의 전파 규칙을 구현함으로써, 모든 사용자와 항목의 표현을 효율적으로 동시에 업데이트 할 수 있으며, 이것은 일반적으로 큰 규모의 그래프에서 그래프 컨볼루션 네트워크를 실행 가능하게 만드는 데 사용되는 노드 샘플링 절차를 버릴 수 있도록 해준다.
[번외] 라플라시안 행렬과 노드 샘플링
라플라시안 행렬을 사용함으로써 노드 샘플링 절차를 수행하지 않아도 되는 이유가 의아해서 알아본 결과 다음의 이유를 따른다고 한다.
노드 샘플링은 그래프 신경망을 대규모 그래프에서 실행 가능하게 만드는 일반적인 방법 중 하나로 대규모 그래프에서 모든 노드를 사용하는 것은 연산적으로 매우 비싸거나 현실적으로 불가능하여 노드 샘플링을 통해 그래프의 일부만 사용하여 모델을 학습하는 방법으로 무작위로 또는 특정 방식으로 노드를 샘플링 하여 계산 비용을 절감한다.
그러나 해당 논문에서 제안된 NGCF에서는 라플라시안 행렬과 같은 그래프 표현을 사용하여 모든 노드와 엣지를 고려할 수 있으며, 이것은 그래프의 연결 정보를 효과적으로 잡아낼 수 있어 노드 샘플링 없이도 그래프를 사용할 수 있도록 한다.
즉, 라플라시안 행렬을 이용하여 그래프를 표현하면 전체 그래프를 표현하더라도 비용이 비교적 덜 들기 때문에 기존에 사용하던 노드 샘플링 방식으로 전체 그래프를 표현할 이유가 없어졌다고 이해했다.
3. Model Prediction
예측 레이어는 다양한 전파 레이어에서 개선된 임베딩을 집계하고 사용자-아이템 쌍의 연관 점수를 출력한다.
최종 임베딩 생성
다층 레이어를 통해 임베딩을 확장한 후 사용자 와 아이템 는 여러 표현을 얻는다.
이러한 표현들은 서로 다른 연결(concatenate)을 통해 전달된 메시지를 강조하며, 사용자의 선호도를 반영하는 데 다양한 기여를 한다.
즉, 다른 층에서 얻은 표현을 연결하여 사용자와 아이템의 최종 임베딩을 생성한다.
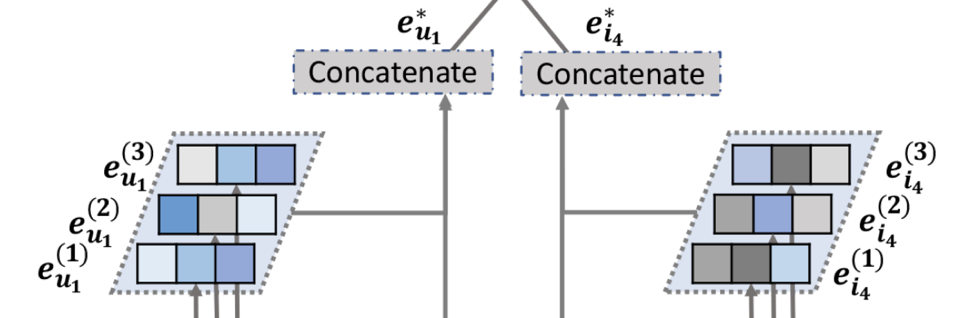
해당 그림의 연결을 수식으로 표현하면 다음과 같다.
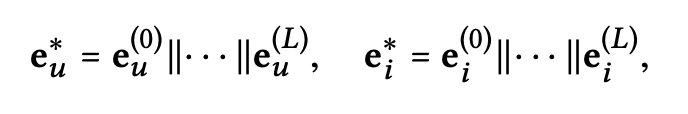
이러한 연결 작업은 초기 임베딩을 임베딩 확장 레이어로 보다 풍부하게 만들어주며,
(레이어의 수)를 조절함으로써 전파 범위를 조절할 수 있다.
추가로 연결 뿐만 아닌 다른 종류의 집계자(aggregator),
예를 들어 가중 평균, 최대 풀링, LSTM과 같은 방법들을 사용할 수 있다.
그 중 연결(concatenate)의 장점은 학습할 추가 매개변수가 없다는 것이다.
선호도 추정
마지막으로 사용자의 대상 아이템에 대한 선호도를 추정하기 위해 내적을 수행한다.
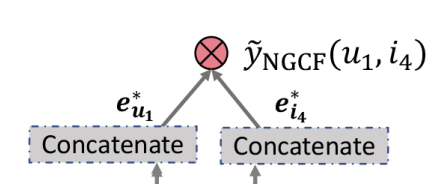
해당 그림의 내적을 수식으로 표현하면 다음과 같다.
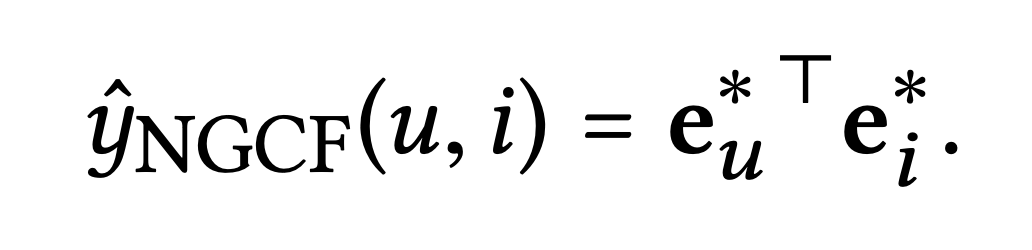
해당 논문에서는 내적과 같은 간단한 상호 작용 함수를 사용하며, 복잡한 상호 작용 함수는 미래 연구로 남긴다.
📖 Optimization
해당 모델은 pairwise BPR loss를 사용한다.
BPR loss는 상호 작용이 관찰된 항목은 낮은 손실 값을 갖도록 하고,
상호 작용이 관찰되지 않은 항목은 높은 손실 값을 갖도록 하여 순위를 고려한다.
손실 함수는 다음과 같이 정의된다
= {}
: 상호 작용이 관찰된 집합
: 상호 작용이 관찰되지 않은 집합
= { {,}} : 학습 가능한 모델 파라미터
: 정규화 강도를 조절하는 하이퍼파라미터
논문은 모델 매개변수를 학습하기 위해 미니배치 Adam 최적화 알고리즘을 사용하며,
에서 무작위로 선택된 삼중자 의 미니배치에 대한 표현을 단계의 전파 후 손실 함수의 그래디언트를 사용하여 모델 매개변수를 업데이트한다.
Message and Node Dropout
NGCF 모델에서는 두 가지 Dropout 기술을 사용한다.
-
Message Dropout : 메시지들을 무작위로 삭제한다.

예를 들어 위의 방정식에서 전파되는 메시지들을 일정 확률 로 드롭 아웃한다.
이로써 번째 전파 계층에서는 일부 메시지만 표현에 기여하게 된다.
이를 통해 사용자와 아이템 간의 연결 유무에 민감한 모델을 보다 안정적으로 만들어준다. -
Node Dropout : 특정 노드를 무작위로 차단하고 해당 노드의 모든 발신 메시지를 삭제한다.
구체적으로 번째 전파 계층에서는 Laplacian Matrix에서 개의 노드를 무작위로 삭제한다.
이를 통해 특정 사용자나 아이템의 영향력을 줄이는 데 도움이 된다.
즉, 두 가지의 Dropout은 모델의 과적합을 방지하기 위한 효과적인 방법이며,
이는 모델 훈련 중에만 사용되고 테스트 중에는 비활성화된다.
📖 Discussions
NGCF Generalizes SVD++
NCF가 MF를 일반화한 경우와 같이 NGCF는 SVD++를 일반화한다.
SVD++는 NGCF의 고차원 전파 레이어를 사용하지 않은 NGCF의 특별한 경우로 볼 수 있다.
이로써 와를 각각 사용자 u와 아이템 i의 최종 표현으로 취급한다.
추가로 전파 레이어 내에서는 변환 행렬과 비선형 활성화 함수를 비활성화한다.
이를 NGCF-SVD 모델이라고 하며 다음과 같이 정의된다.
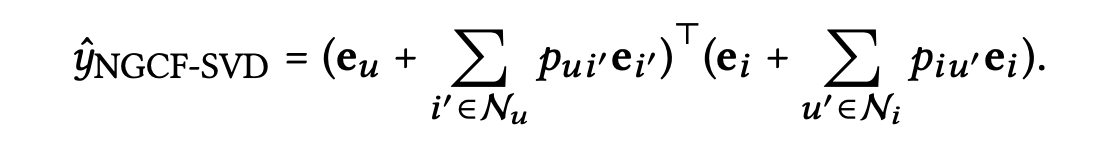
와 를 각각 와 으로 설정함으로써 SVD++ 모델을 정확하게 재현할 수 있다.
📖 Experiments
1. Performance Comparison
Overall Comparison
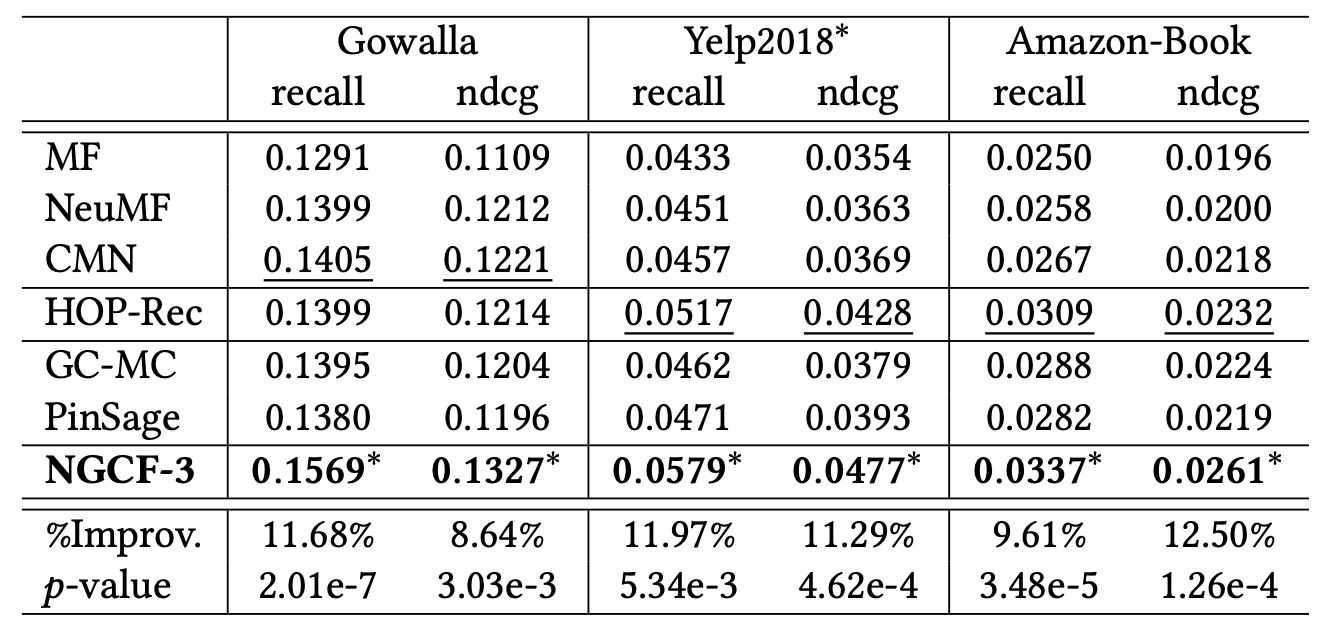
NGCF는 모든 데이터셋에서 일관되게 가장 우수한 성능을 보이며,
One-Sample t-tests를 통해 이러한 향상이 통계적으로 유의미함을 보여준다.
Performance Comparison w.r.t. Interaction Sparsity Levels
상호 작용 희소성 문제가 추천 시스템의 표현 능력을 제한하는 경우가 있음을 언급한다.
비활성화 사용자의 적은 상호 작용은 고품질 표현을 생성하기에 충분하지 않을 수 있다.
하지만 연결 정보를 활용하면 이러한 문제를 완화할 수 있음을 해당 실험을 통해 주장한다.
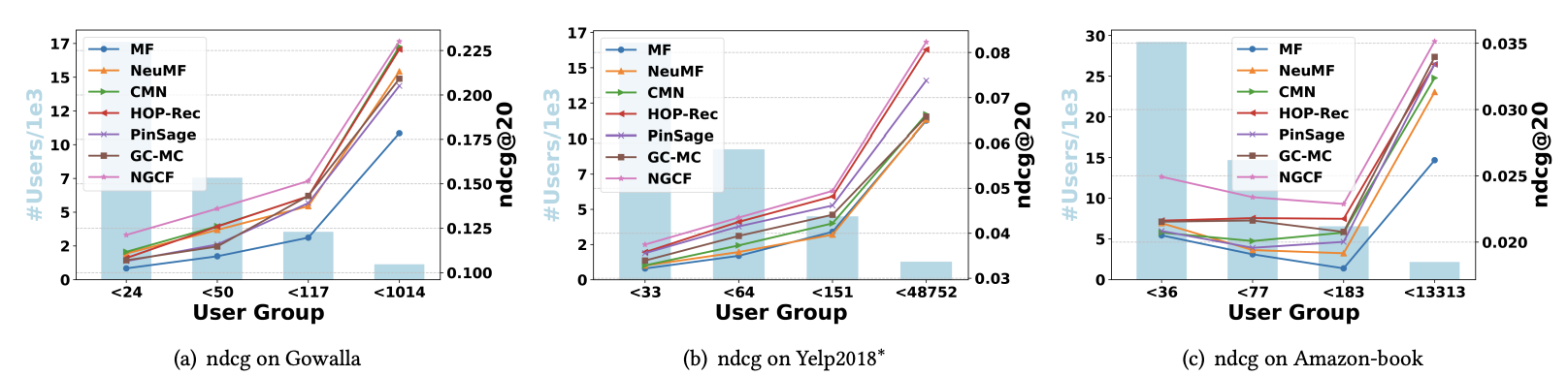
실험은 사용자 당 상호 작용 수에 기초하여 테스트 세트를 네 개의 그룹으로 나눈다.
Gollwalla 데이터 셋을 예로 들면, 사용자 당 상호 작용 수가 각각 24 미만, 50 미만, 117 미만, 1014 미만임을 의미한다.
-
NGCF와 HOP-Rec은 모든 사용자 그룹에서 다른 모델들을 지속적으로 능가한다.
이는 고차 연결성을 활용하면 비활성 사용자의 표현 학습을 크게 촉진할 수 있음을 보여준다.
이는 협업 신호가 효과적으로 포착될 수 있기 때문에 추천 시스템의 희소성 문제를 해결할 수 있는데 유망할 수 있음을 보인다. -
그림 (a), (b), (c)를 함께 분석하면 첫 번째 두 그룹 (예 : Gowalla의 <24, <50)이 뒤의 두 그룹 (예 : Gowalla의 <117, <1014)에 비해 다른 모델과의 ndcg 비교 값이 크다는 것을 알 수 있고, 이는 임베딩 전파가 비교적 비활성 사용자에게 이점이 있음을 보인다.
2. Study of NGCF
Effect of Layer Numbers
다양한 레이어 수 (1, 2, 3, 4)를 사용하여 모델을 생성하고 레이어의 영향을 조사한다.
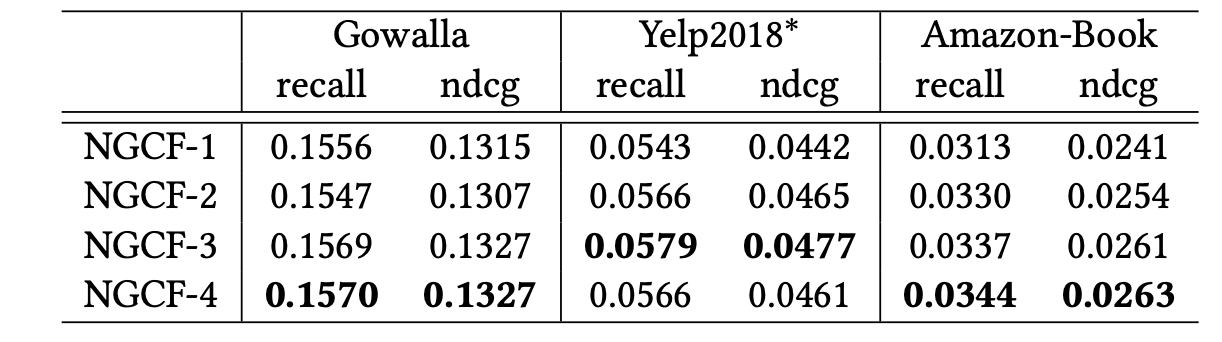
1. NGCF의 레이어 수를 증가시키면 추천 성능이 상당히 향상된다.
2. NGCF-4는 Yelp2018* 데이터셋에서 과적합을 초래함을 발견한다.
이는 너무 깊은 아키텍처를 적용하면 표현 학습에 노이즈를 포함함으로써 과적합이 발생할 수 있으며, 다른 두 데이터셋에서 또한 4개의 층이 미미한 개선을 불러오는 것을 통해 3개의 전파 레이어를 사용하는 것이 협업 필터링 신호를 캡처하는 데 충분함을 확인한다.
Effect of Embedding Propagation Layer and Layer Aggregation Mechanism
Embedding Propagation Layer와 Layer Aggregation Mechanism이 성능에 어떤 영향을 미치는지 조사하기 위해 NGCF-1의 변형 버전을 고려한다.
노드와 그 이웃간의 표현 상호작용을 메시지 전달 함수에서 제거하고, Pinsage 및 GC-MC와 동일하게 설정한다.
다음의 버전을 각각 및 라고 한다.
추가로 SVD++을 기반으로 한 변형 버전을 라고 한다.
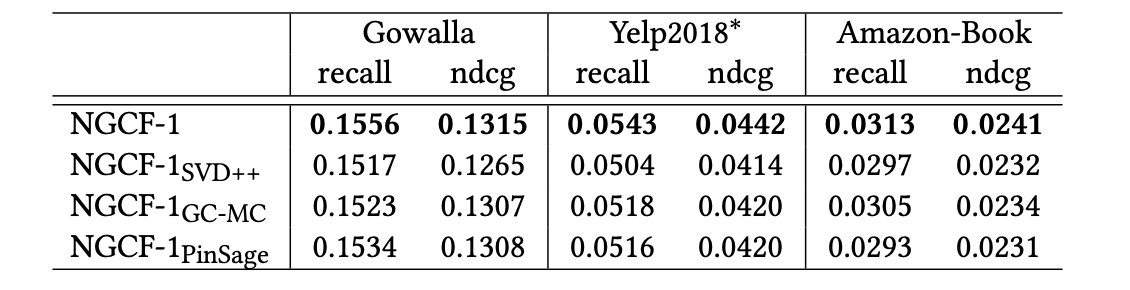
- NGCF-1이 모든 변형 버전에 비해 일관되게 우수한 성능을 보인다.
이는 표현 상호 작용이 메시지 전파를 통해 전파되는 메시지가 와 간의 유사성에 의존하고 Attention Mechanism과 같은 기능을 수행하기 때문이다.
다른 모든 변형 버전은 선형 변환만 고려한다. - 대부분의 경우에서, 는 및 보다 성능이 떨어지는데 이는 노드 자체가 전달하는 메시지와 비선형 변환의 중요성을 보여준다.
- 및 가 각각 Pinsage 및 GC-MC보다 더 나은 성능을 달성한다는 것을 알 수 있는데 이는 레이어 집계 메커니즘의 중요성을 강조한다.
Effect of Dropout
NGCF 모델에서 오버피팅을 방지하기 위해 Node Dropout과 Message Dropout 기술을 사용한 효과에 대해 다룬다.
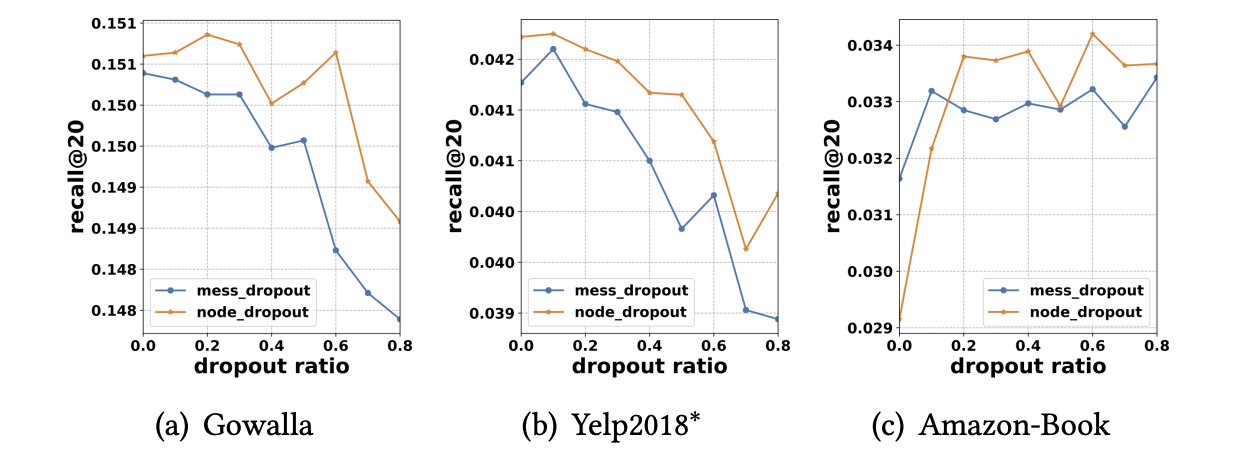
- 실험을 통해 Dropout을 사용했을 때 평가 지표 recall의 수치가 향상되었음을 보인다.
- NGCF 모델에서 오버피팅을 방지하기 위해 노드 드롭아웃이 메시지 드롭아웃보다 효과적인 것으로 나타난다.
Test performance w.r.t. Epoch
MF 모델과 NGCF 모델 각각의 Epoch에 대한 테스트 성능을 나타낸다.
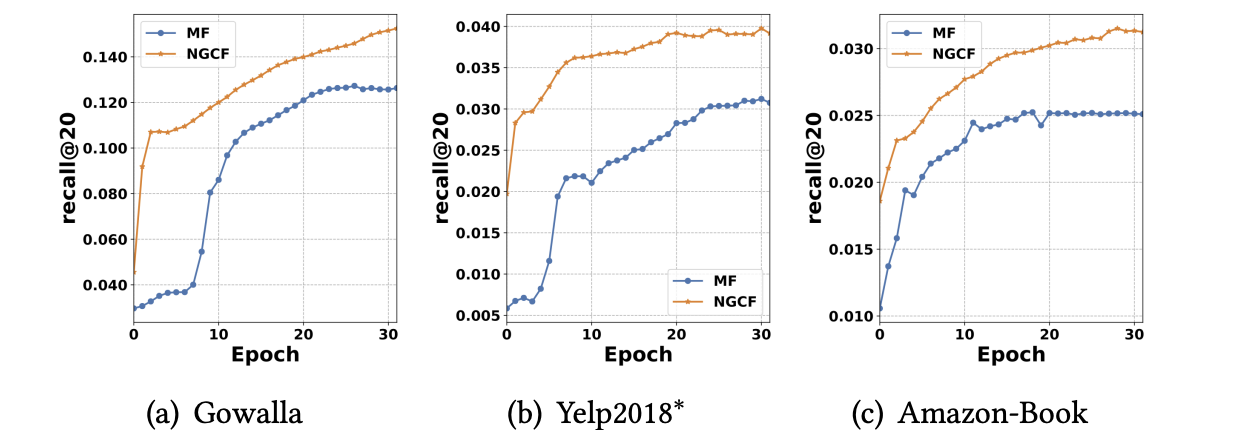
NGCF는 세 데이터셋에서 MF보다 빠른 수렴을 보인다.
즉, 빠른 수렴은 적은 Epoch으로 높은 성능의 모델을 만들 수 있음을 의미한다.
3. Effect of High-order Connectivity
임베딩 전파 레이어가 임베딩 공간에서 표현 학습을 어떻게 용이하게 하는지 보여준다.
이를 위해 Gowalla 데이터 셋에서 무작위로 선택한 6명의 사용자와 그와 관련된 아이템들에 대해 조사한다.
다음 그림은 각각 MF(즉, NGCF-0) 및 NGCF-3서 파생된 표현의 시각화를 보여준다.
여기서 항목들은 테스트 세트의 것으로, 훈련 단계에서 사용자와 짝지어지지 않은 항목들이다.
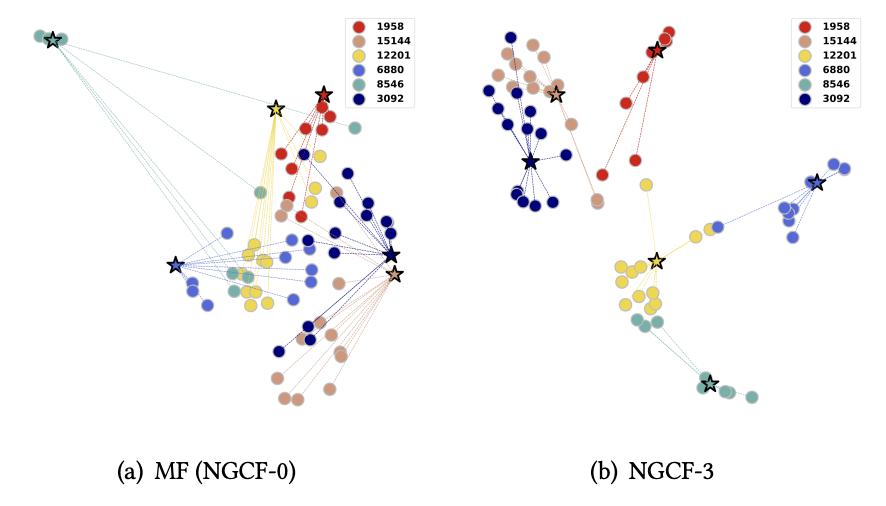
- NGCF-3의 표현은 비교적 구별 가능한 클러스터링을 보여줌으로써 사용자와 아이템 간의 연결성이 임베딩 공간에 잘 반영됨을 알 수 있다.
- 동일한 사용자를 위의 그림에서 비교할 때, NGCF-3에서 사용자와 사용자의 과거 아이템의 임베딩이 비교적 더 가까이 위치해있는 경향이 있다.
이는 임베딩 전파 레이어가 명시적인 협업 신호를 표현에 주입할 수 있는 능력이 있는 것을 입증한다.
📖 Conclusion
해당 논문의 내용에 대한 정리는 Abstract 및 Introduction에서 여러번 언급했다고 생각하기에 저자가 남겨둔 추가 연구 사항을 정리하며 마무리한다.
- Attention Mechanism : Attention Mechanism을 도입하여 임베딩 전파 중 이웃들에 대한 가중치를 학습하고 다양한 순서의 연결성에 대한 가중치를 조절하는 것으로 NGCF를 개선할 수 있다.
- Adversarial Learning : 사용자/아이템 임베딩 및 그래프 구조에 대한 적대적 학습을 탐구함으로써 모델의 강건함을 높인다.
- 구조적 지식 확장 : 아이템 지식 그래프를 사용자-아이템 그래프와 통합하여 사용자와 아이템 간의 지식 기반 연결성을 확립할 것을 제안한다.
이는 사용자가 아이템을 선택하는 의사 결정 과정을 밝혀내는 데 도움이 될 수 있다.