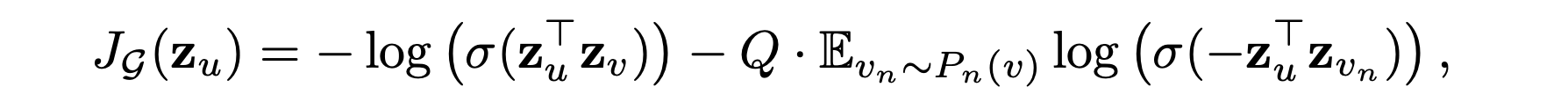[논문 리뷰] Inductive Representation Learning on Large Graphs

태환·2023년 11월 17일

Paper

Paper Review

목록 보기

4/15

📌 Inductive Representation Learning on Large Graphs

📖 Abstract

기존 그래프의 노드에 대한 저차원 임베딩 방법은 대부분 임베딩 훈련 중 그래프의 모든 노드가 존재해야 한다는 조건이 있으며, 본질적으로 transductive하여 새로운 노드에 대해 일반화되지 않는다는 한계점이 존재한다.
GraphSAGE는 노드 특징 정보를 활용하여 새로운 데이터에 대한 노드 임베딩을 효율적으로 생성하는 inductive 프레임워크이다.
각 노드에 대해 개별 임베딩을 훈련하는 대신, 각 노드의 지역 이웃에서 특징을 샘플링하고 집계하여 임베딩을 생성하는 함수를 학습한다.

즉, GraphSAGE는 기존의 GCN 방법론에서 다음의 두 가지 사항을 개선했다.

노드 임베딩 과정에서 모든 노드를 필요했던 기존 방법론과 달리 각 노드의 지역 이웃만을 필요로하게 만들었으며, 샘플링을 통해 메모리 요구량을 줄였다.
transductive한 기존 방법론과 달리 inductive한 방법론을 제시하여 새로운 노드에 대한 임베딩을 효율적으로 생성할 수 있게 만들었다.

📖 Background

inductive & transductive learning

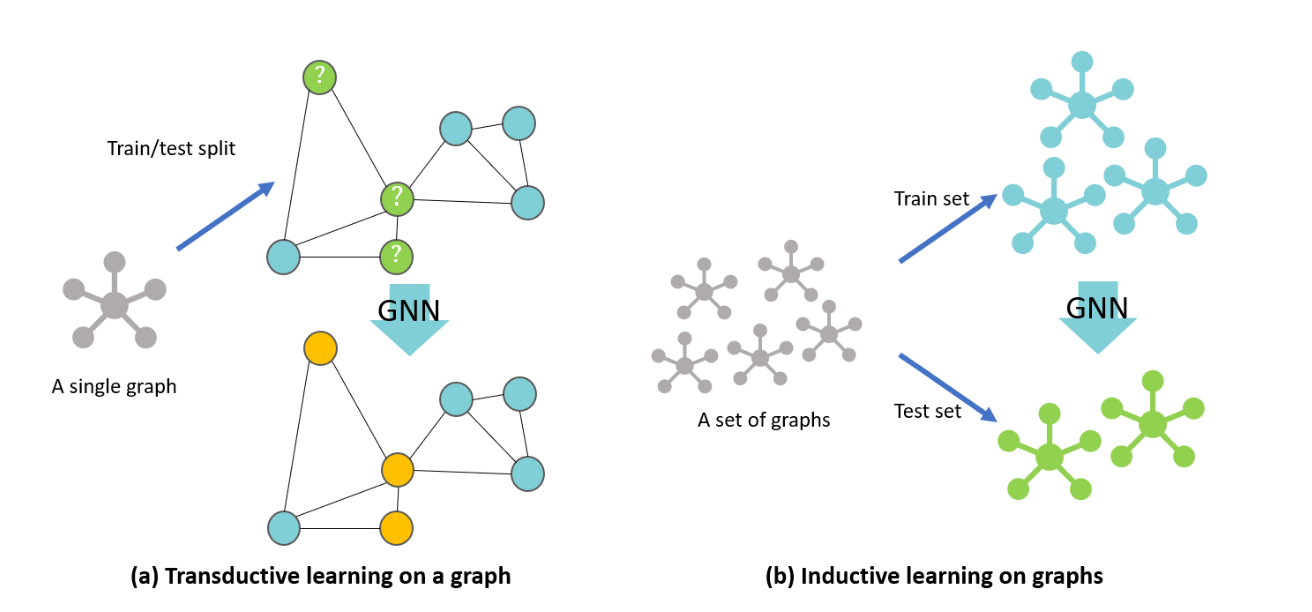
inductive learning : 전통적인 지도 학습 방식으로 머신러닝 모델을 설계한 뒤 train dataset을 통해 분류 혹은 회귀를 위한 규칙을 추론하여 새로운 데이터가 들어왔을 때 예측하는데 사용한다.
transductive learning : train dataset 뿐만 아니라 label 정보가 없는 test dataset도 주어지며, 머신러닝 모델을 설계한 뒤 train dataset의 특징 정보와 label 정보 그리고 test dataset의 특징 정보를 통해 주로 분류를 위한 규칙을 추론하여 가지고 있는 test dataset의 label 정보를 예측하는데 사용한다.

해당 논문은 대규모 그래프를 다루며, 다양한 데이터에 대응해야하는 산업 현장에 기여하기 위해 inductive 방법론을 제시한다.

inductive & transductive learning에 관한 자세한 설명이 담긴 블로그 링크를 Reference에 남겼다.

📖 Introduction

대규모 그래프의 노드에 대한 낮은 차원의 벡터 임베딩은 다양한 예측 및 그래프 분석 작업에 매우 유용하게 활용되고 있다.

이전 연구들은 주로 단일 고정된 그래프(transductive learning)에 중점을 두었지만, 현실 세계 응용 프로그램에서는 빠르게 임베딩을 생성하거나 완전히 새로운 그래프에 대한 요구사항이 있다.

이러한 inductive 능력은 지속적으로 보이지 않는 노드를 다루는 고처리량의 기계 학습 시스템에서 특히 중요하며, 이를 통해 동일한 형태의 특징을 가진 그래프간에 일반화를 쉽게 할 수 있다.

본 연구는 GCN을 inductive 비지도 학습 작업으로 확장하며, 학습 가능한 집계 함수를 사용하여 간단한 convolution을 초과하는 기능으로 확장한다.

Factorization-based embedding approaches

기존의 노드 임베딩 방법론인 factorization-based embedding 방식은 random walk statistics 및 행렬 분해 기반의 학습 목표를 사용하여 저차원 임베딩을 학습하는 여러 방법이 있다.

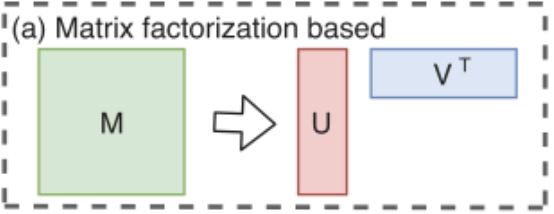
이 임베딩 알고리즘은 개별 노드에 대한 노드 임베딩을 직접 훈련하기 때문에 본질적으로 transductive이며, 새로운 노드에 대한 예측을 수행하려면 추가로 비용이 많이 드는 훈련이 필요하다.

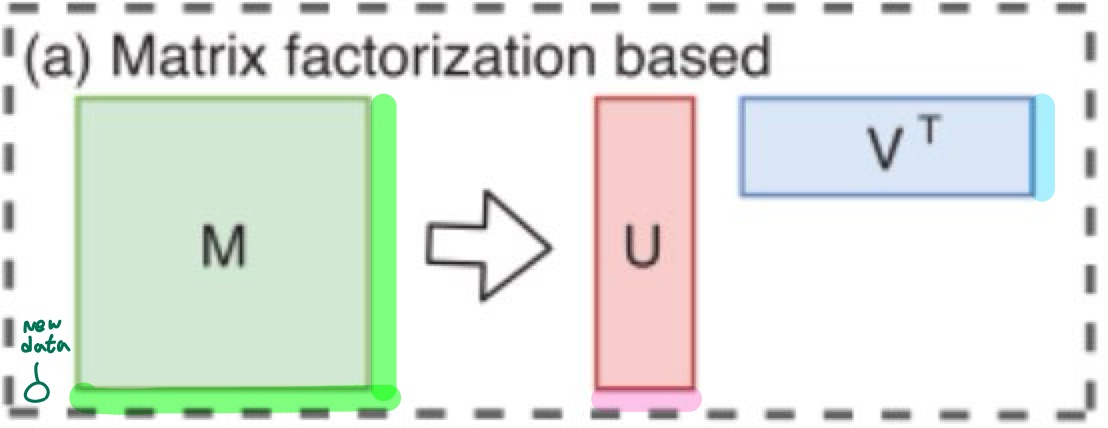
위와 같은 factorization-based embedding 방식은 새로운 노드가 추가되면 기존 행렬에 새로운 노드의 정보를 입력해야 하며, 이로 인해 최적화된 가중치 행렬의 값도 영향을 받게된다.
즉, 새로운 노드를 고려하기 위해 전체 모델이 처음부터 다시 최적화되어야 하며 이는 transductive model의 한계점이다.

이러한 방식과 달리 GraphSAGE는 기존 노드의 특징 정보를 활용하여 모델을 훈련시키고, 이를 통해 새로운 노드에 대한 임베딩을 생성한다.

📖 GraphSAGE

1. Embedding generation

이는 mini-batch가 적용된 GraphSAGE 알고리즘이다.
설명은 mini-batch 부분과 임베딩 노드의 표현부분으로 나누어 진행한다.
대규모 그래프에서 mini-batch를 사용하는 이유와 GNN에서 mini-batch를 적용하는 방식에 대한 설명은 링크를 참고하면 좋을 것 같다.

두 링크의 내용을 간단히 정리하면 대규모 그래프에서는 GPU 용량의 문제로 full-batch를 사용할 수 없으며, 다음의 그림처럼 GNN에서는 기존의 mini-batch와 다르게 하나의 노드를 하나의 batch로 간주한다.

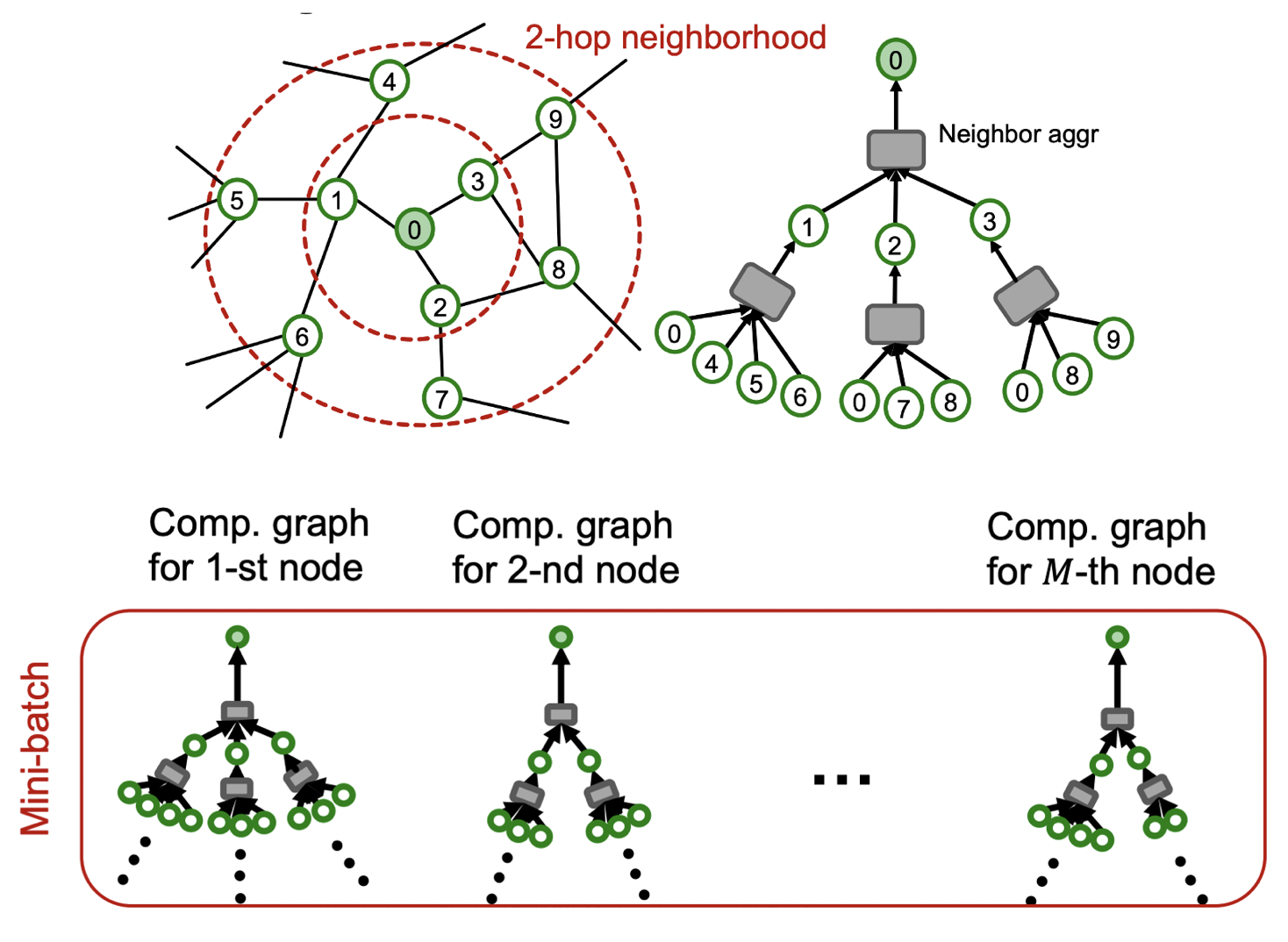
1. 위 그림의 그래프를 기반으로 미니 배치 정의 부분을 정리하면 다음과 같다.

( batch = 1, K = 2로 가정)

$0_{node}$ 을 기준으로 $1$ -hop 이웃을 샘플링한다.
$N(0_{node}$ ) = [ $1_{node}$ , $3_{node}$ ] -> $B^1 = [0_{node},$ $1$ -hop 이웃 : [ $1_{node}, 3_{node}$ ]]
여기서 노드를 샘플링하는 방식은 uniform 분포로 랜덤하게 고를 수도 있고,
사전에 노드마다 가중치를 설정해 높은 가중치를 갖는 노드를 샘플링할 수도 있다.
추가로 샘플링하는 이웃의 수는 각 $l$ -hop 마다 변경할 수 있다.
$0_{node}$ 을 기준으로 $2$ -hop 이웃을 추가로 샘플링한다.
$N(0_{node}$ ) = [ $1_{node}$ , $3_{node}, N(1_{node}), N(3_{node})$ ]
-> $B^0 = [0_{node},$ $1$ -hop 이웃 : [ $1_{node}, 3_{node}$ ], $2$ -hop 이웃 : [ $4_{node}, 5_{node}, 8_{node}, 9_{node}$ ]]

사실 알고리즘을 해석하면 미니 배치 이웃의 정의는 가장 먼 hop에 있는 이웃부터 정의되어 가까운 hop으로 진행되지만, 이해의 편의를 돕고자 1번과 2번 과정의 순서를 바꿨다.

위의 과정을 통해 얻게되는 노드 0을 타겟으로 한 미니 배치는 $B^0$ 이며,
설정한 mini-batch 갯수 만큼의 각기 다른 노드들의 미니 배치를 얻게된다.

샘플링은 다음의 그림과 같이 표현할 수 있다.

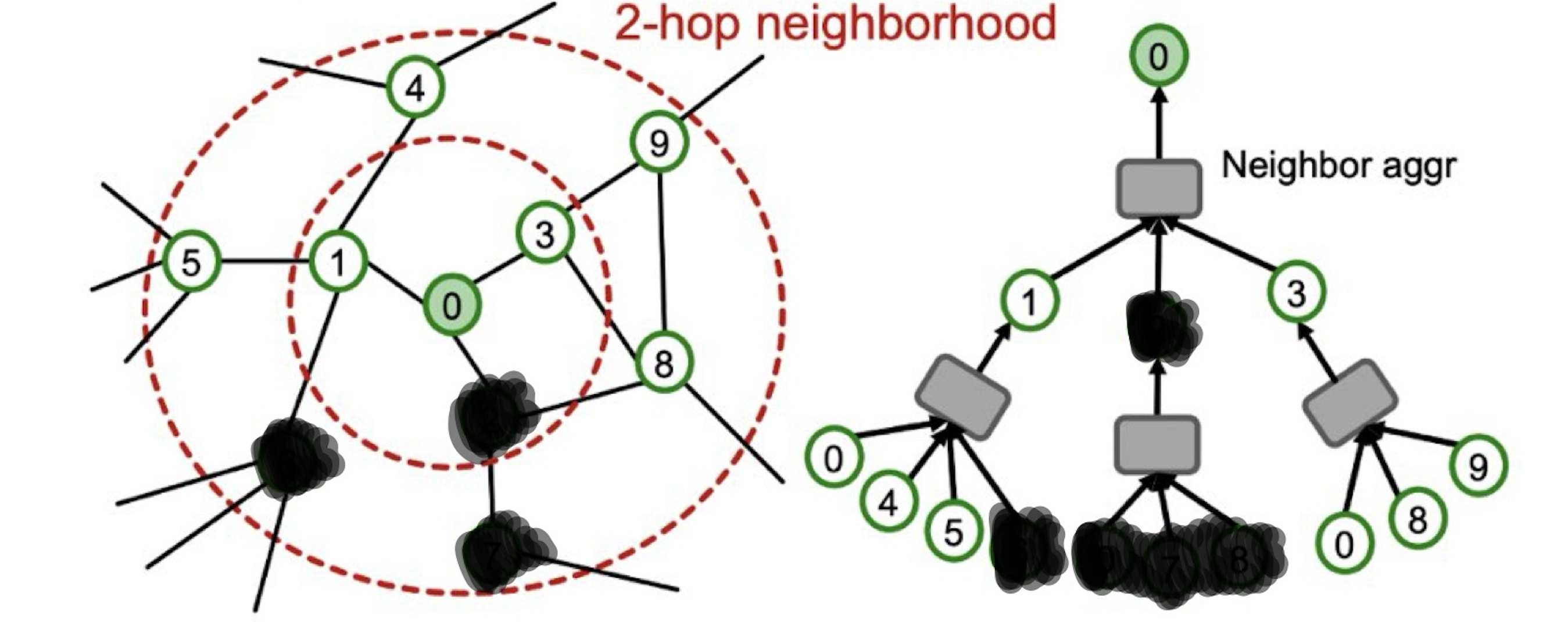
2. mini-batch로 정의 된 노드의 임베딩 표현 부분을 정리하면 다음과 같다.

사실 위의 오른쪽 그림이 집계되는 과정을 잘 표현하고 있다.

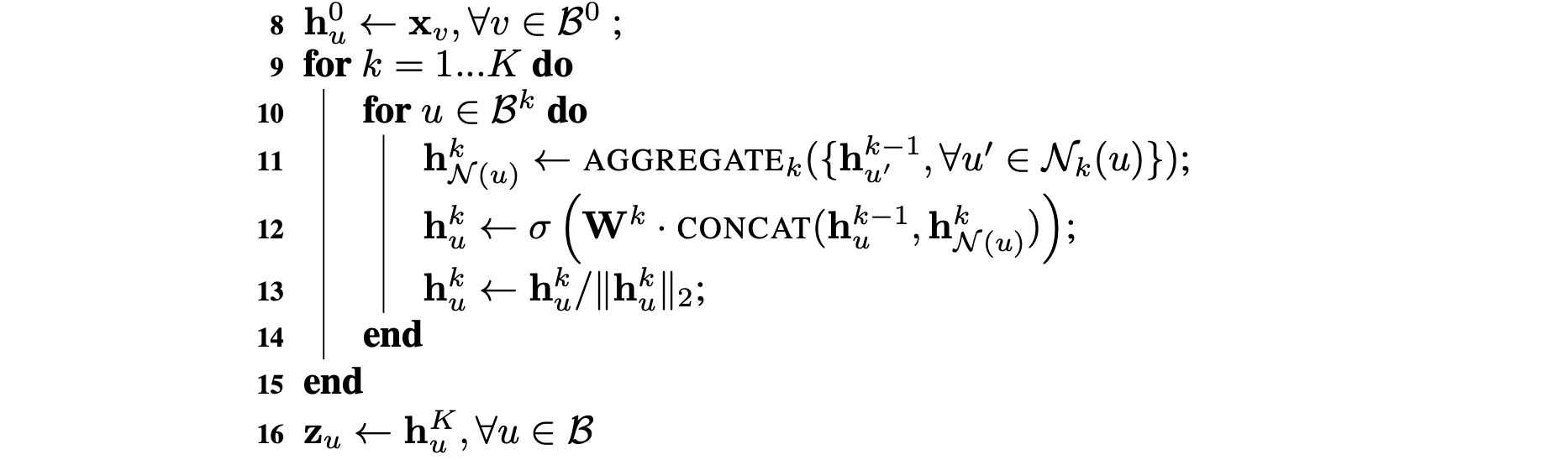
반복 $k$ 에서 각 노드 $v∈V$ 는 $(k-1)$ -hop에 있는 이웃 노드들의 표현을 하나의 벡터 $h^k_{N(v)}$ 로 집계한다.
이웃 노드의 특징 벡터를 집계한 후, 알고리즘은 노드의 현재 표현 벡터 $h^{(k-1)}_v$ 를 1번 과정에서 이웃 벡터를 집계한 벡터 $h^k_{N(v)}$ 와 연결한다.
해당 연결 벡터는 비선형 활성화 함수 $σ$ 를 사용한 fully connected layer를 통과한다.
이 레이어의 출력은 알고리즘의 다음 단계에서 사용될 노드 표현이 된다.
이러한 과정이 반복되어 모든 mini-batch 노드들에 적용되며, 각 노드들의 임베딩 벡터를 생성한다.

2. Learning the parameters

예측적인 표현을 비지도 설정에서 학습하기 위해 출력 표현인 $z_u$ 에 대해 그래프 기반 손실 함수를 적용하고, 가중치 행렬 $W_k$ 및 집계 함수의 매개변수를 확률적 경사 하강법을 통해 조정한다.
그래프 기반 손실 함수는 근처 노드가 유사한 표현을 가지도록 장려하면서 떨어진 노드의 표현이 다르도록 강제한다.

$Denote$
$v$ : 노드 $u$ 기준 고정 길이의 랜덤 워크 내에서 동시에 존재하는 노드들
$P_n$ : 부정적인 샘플링 분포
$Q$ : 부정적인 샘플의 수

3. Aggregator Architectures

노드의 이웃에는 순서가 존재하지 않기 때문에 집계 함수는 정렬되지 않은 벡터 집합 상에서 작동해야 한다.
저자는 세 가지 후보 집계 함수를 언급한다.

1. Mean Aggregator

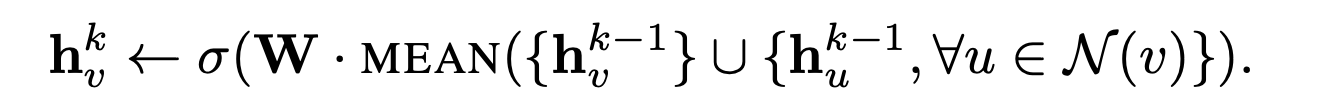
간단한 평균 계산으로 이웃 벡터의 평균을 계산한다.
수정된 평균 기반 집계 함수를 "컨볼루션"이라고 부르며, 컨볼루션 함수는 다른 제안된 함수와 달리 이전 레이어의 표현과 이웃 벡터의 연결을 하지 않는다는 것이다.
이는 성능에 상당한 이득을 가져온다고 한다.

2. LSTM Aggregator
LSTM은 입력을 순차적으로 처리하기 때문에 이웃 노드의 순서를 고려하게 된다.
이를 해결하기 위해 이웃 노드들의 임의 순열을 만들어 LSTM에 적용했다.
평균 기반 집계 함수와 비교하여 LSTM은 더 큰 표현 능력을 가진다.

3. Pooling Aggregator

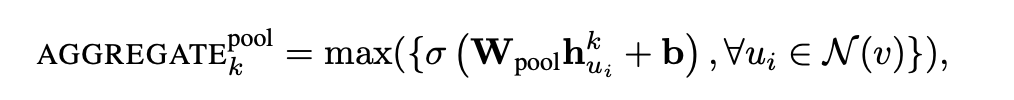
최대 또는 평균 풀링을 통해 이웃 벡터를 집계한다.
해당 풀링 접근 방식에서는 각 이웃의 벡터가 독립적으로 fully connected layer를 통과한 다음, 이웃 집합 전체에서 정보를 집계하기 위해 원소별 최대 풀링 연산이 적용된다.
따라서 해당 집계 함수는 훈련 가능한 특성을 가지고 있다.
실험 부분에서는 최대와 평균 풀링 간에 유의미한 차이를 찾지 못하여 주로 최대 풀링을 사용했다고 한다.

📖 Experiments

1. Performance of GraphSAGE

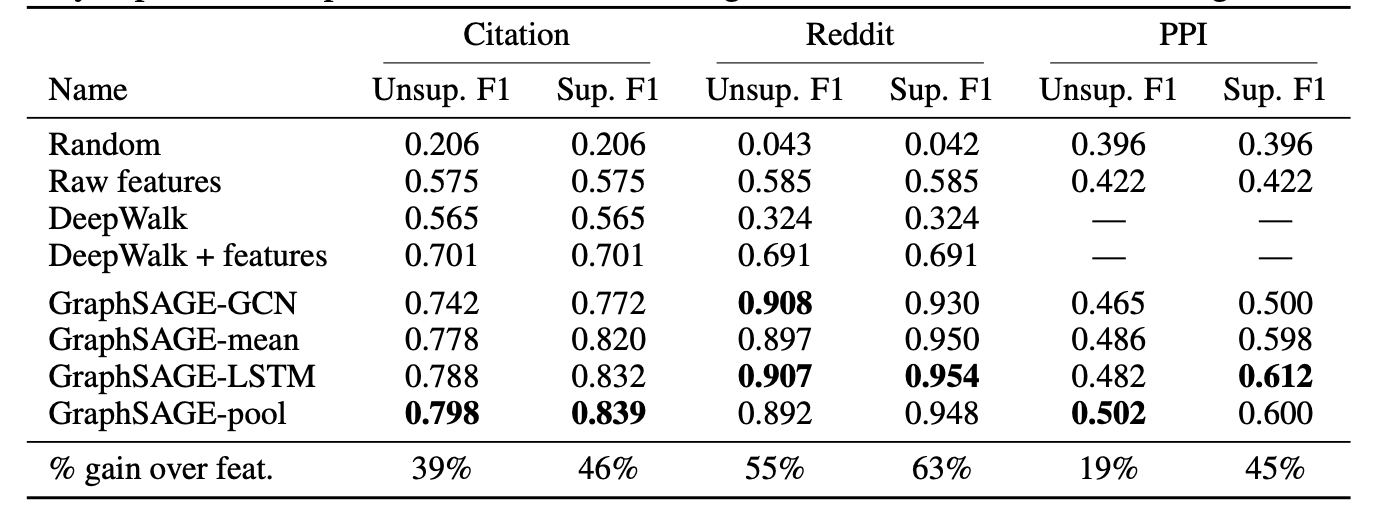
3가지 데이터 셋 모두에서 GraphSAGE는 다른 임베딩 방법론에 비해 높은 성능을 보인다.
주목할만한 점은 기존 DeepWalk 방법론에 feature 정보를 더함으로써 성능이 비교적 눈에띄게 향상했음을 알 수 있다.

2. Runtime and parameter sensitivity

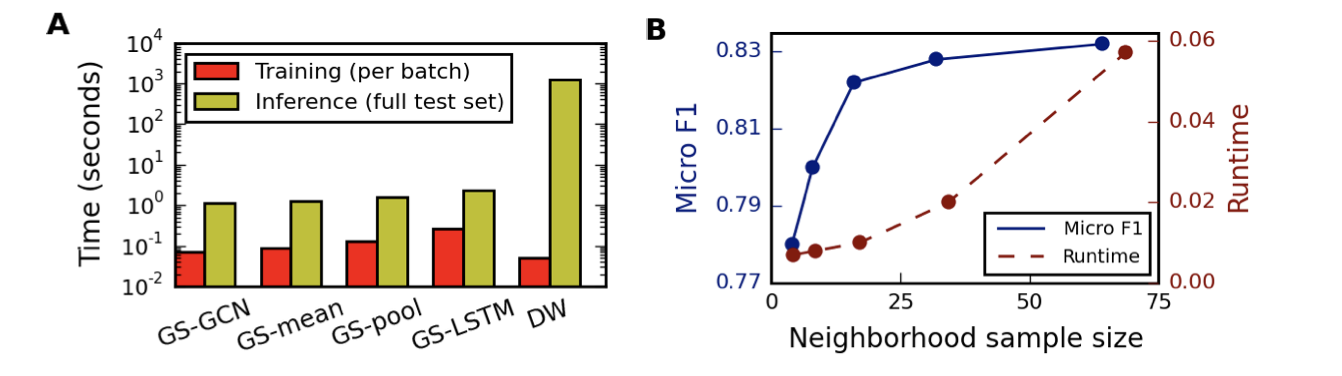
Figure $A$ 는 다양한 접근 방식에 대한 훈련 및 테스트 런타임을 요약한다.
각 방법의 훈련 시간은 비슷하지만 DeepWalk는 테스트 시간에 100~500배 느리다.
GraphSAGE 변형에 대해서 K = 2로 설정하면 K = 1대비 평균적으로 약 10~15%의 정확도 향상이 일관되게 나타났다고 한다.
하지만 K를 2 이상으로 증가시키면 성능이 0~5% 향상하는데 비해 런타임은 10-100배로 막대한 비용이 발생하기에 K = 2로 설정하는 것이 바람직해 보인다.
Figure $B$ 는 다양한 이웃 sample 수에 따른 모델의 성능을 요약한다.
이웃의 수를 대략 25까지 늘리는 과정에서는 성능의 수치가 급격히 늘어나는 반면 런타임은 비교적 조금 늘어나 보이지만, 이웃의 수를 25 이상으로 늘리면 모델의 성능 대비 런타임이 비교적 눈에 띄게 증가하기에 이웃의 sample 수는 약 25 근방의 수가 적당해 보인다.

📖 Conclusion

GCN을 실제 산업에 적용할 수 있도록 inductive model로 개선했다는 점이 인상깊다.
본 논문을 리뷰하는 과정에서 inductive learning & transductive learning을 보다 명확히 학습할 수 있었으며, graph에 적용되는 mini-batch 방식 또한 배울 수 있었다.