알고리즘 계산 복잡도의 척도 2가지
- 시간 복잡도: 얼마나 빠르게 실행되는지
- 공간 복잡도: 얼마나 많은 저장 공간이 필요한지
실행 시간이 짧고, 저장 공간도 적게 쓰는 알고리즘이 좋은 알고리즘
- 통상 둘 다를 만족시키기는 어려움
- 시간과 공간은 반비례적 경향이 있음
- 최근 대용량 시스템이 보편화되면서, 공간 복잡도보다는 시간 복잡도가 우선
- 따라서 알고리즘은 시간 복잡도가 중심
시간복잡도 (Time Complexity)
- 수행 시간은 실행환경에 따라 다르게 측정되기 때문에, 기본 연산의 실행 횟수로 수행 시간을 평가
기본 연산의 종류
- 데이터 입출력 - copy, move...
- 산술 연산 - add, multiply ...
- 제어 연산 - if, while ...
- 시간복잡도는 Best Case(Big-Ω Notation), Worst Case(Big-O Notation), Average Case(Big-θ Notation) 세 종류가 있는데 이 중, Worst Case로 알고리즘의 성능을 파악
- 아무리 최악이라도 이정도의 성능은 보장한다는 의미로 Big-O Notaion을 사용
Worst Case의 Big-O Notation
- 연산 횟수가 다항식으로 표현될 경우, 최고차항을 제외한 모든 항과 최고차항의 계수를 제외시킴
예시
T(n) = n^2+2n+1 = O(n^2) : 최고차항만 나타냄
T(n) = 2n = O(n) : 최고차항의 계수를 제외
T(n) = 4n+3 = O(n)int func (int n) { int sum = 0; // 대입연산 1회 int i = 0; // 대입연산 1회 for(i=0; i<n; i++) { // 반복문 n회 sum += i; // 덧셈 연산 n회 } for(i=0; i<n; i++) { // 반복문 n회 sum += i; // 덧셈 연산 n회 } return sum; // 리턴 1회 }
시간복잡도 단계: 반복문이 지배한다
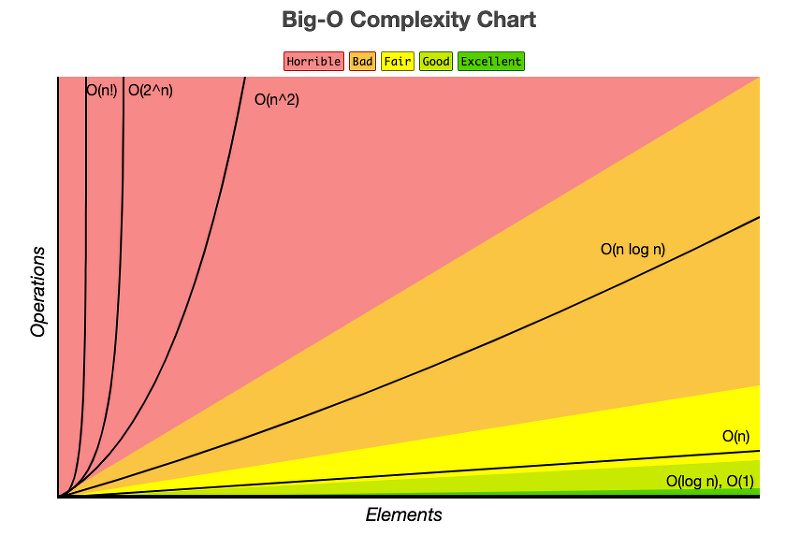
O(n^2): horrible
- 이중반복문의 경우
- ex) bubble sort, insertion sort, selection sort
O(n*logn): bad
- merge sort
O(n): fair
- 변수값에 정비례하여 연산횟수가 증가할 경우
O(1): excellent
- 변수값에 영향을 받지 않고 연산이 상수회 실행될 경우
공간복잡도 (Space Complexity)
- 프로그램을 실행 및 완료하는데 필요한 저장공간의 양
- 총 필요 저장 공간
- 고정 공간 (알고리즘과 무관한 공간): 코드 저장 공간, 단순 변수 및 상수
- 가변 공간 (알고리즘 실행과 관련있는 공간): 실행 중 동적으로 필요한 공간
- S(P) = c + S_p(n)
- c: 고정 공간
- S_p(n): 가변 공간
빅 오 표기법을 생각해볼 때, 고정 공간은 상수이므로 공간 복잡도는 가변 공간에 의해 좌우됨
공간복잡도 구하기 (예시: factorial)
case 1: 변수에 계속 곱하는 방식
public static int factorial1(int n){
int fac = 1;
while (n>0){
fac = fac * n;
n--;
}
return fac;
}이때 공간복잡도는 O(1), n의 값에 상관없이 항상 변수 n과 fac이 저장될 공간이 필요함
case 2: 재귀함수로 곱하는 방식
public static int factorial2(int n){
if(n>0){
return n * factorial2(n-1);
}else{
return 1;
}
}이때 공간복잡도는 O(n), 재귀함수므로 변수 n에 따라 method가 호출되는 횟수(스택에 쌓이는 양) 달라짐.
출처
https://yoongrammer.tistory.com/79
http://bigocheatsheet.com/