Intrinsic time and direciontal changes
Physical time vs. Intrinsic time
- Physical time
- point-based
- daily, hourly,...
- Traditional approachs to observe price movements in financial time series are based on physical time changes
- It has become difficult and challenging to obeserve using this. Why?
- Significant patterns of the trading activity are ignored when using physical time
- Intrinsic time
- event-based
- What is event?
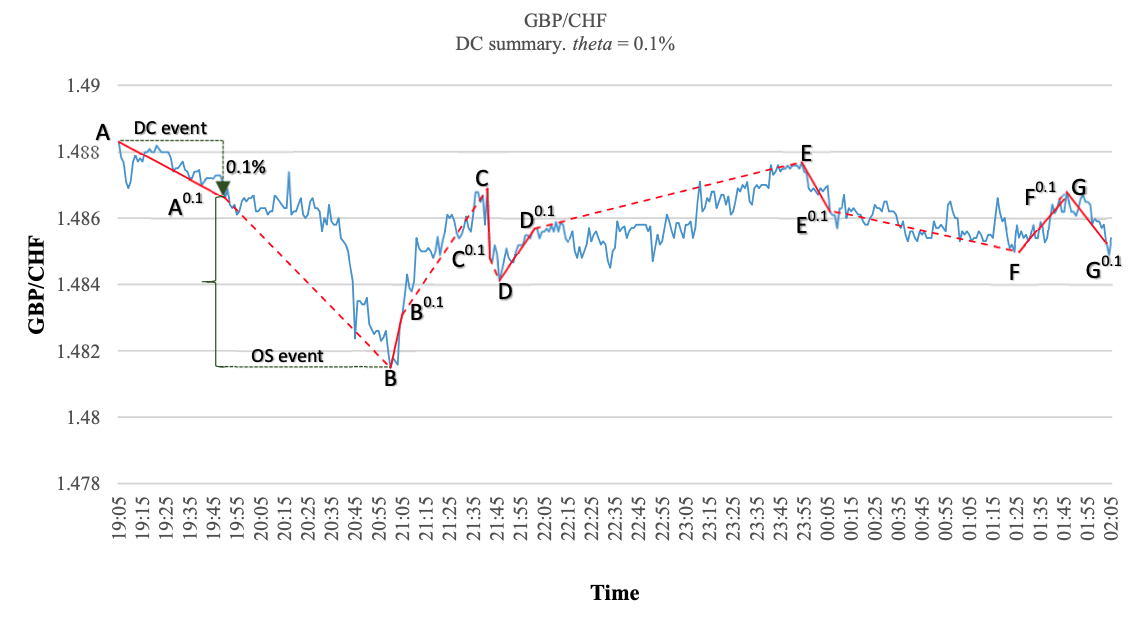
- an event is characterized by a fixed threshold
- is defined as the absolute price change between two local extremal values exceeding a given threshold
- Directional changes are used to define event
- Physical time vs. Intrinsic time
| Physical time | Intrinsic time |
|---|---|
| point-based | event-based |
| homogeneous | inhomogeneous |
| time scales equally spaced | time triggers only at periodic events |
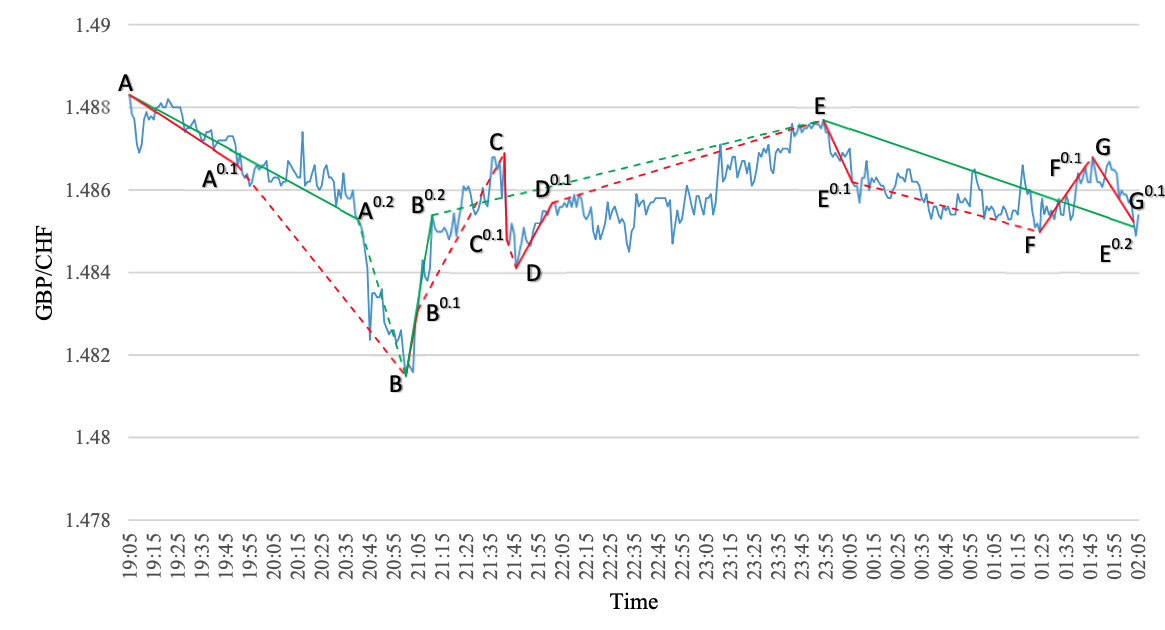
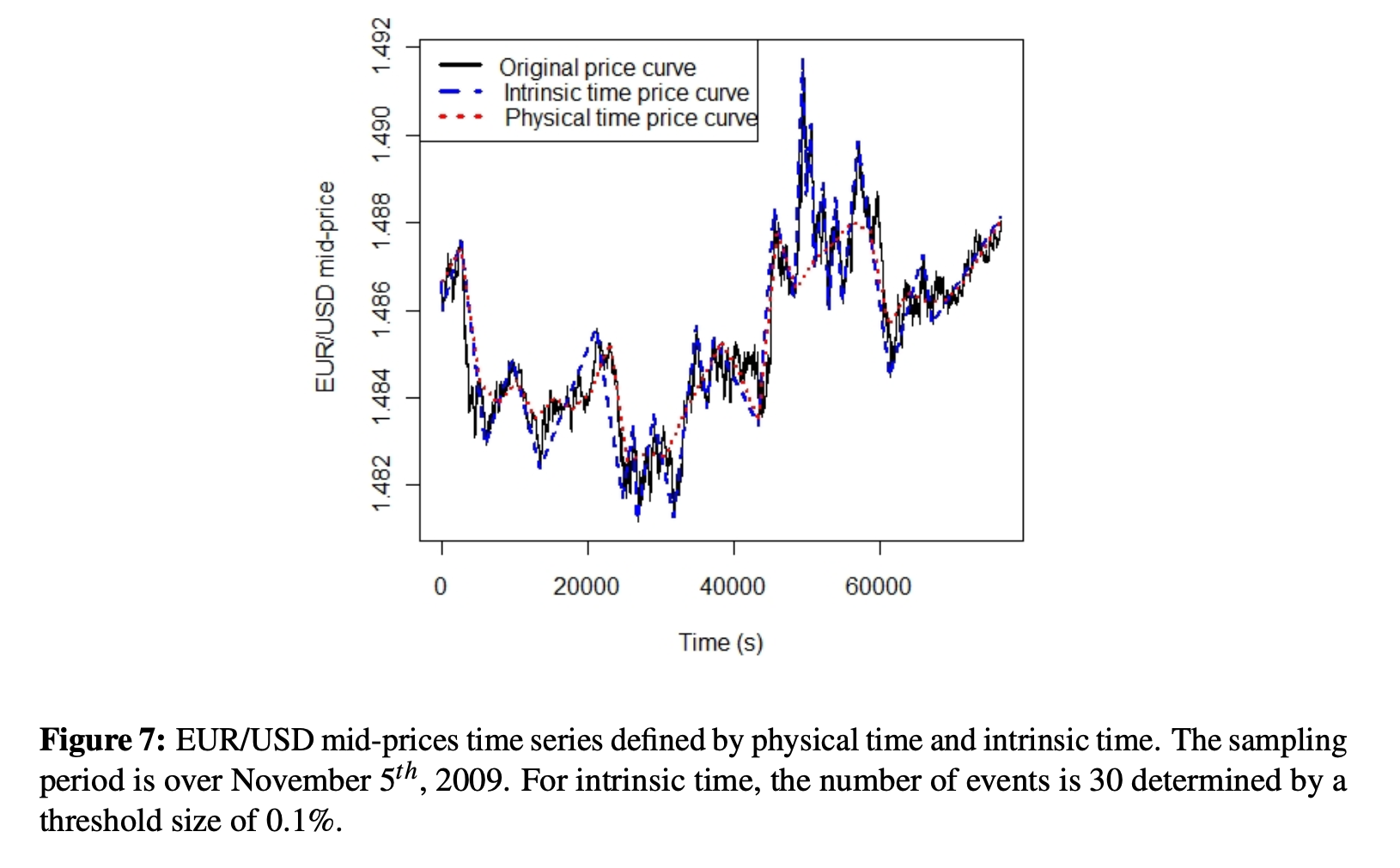
- See Figure below:
- The lines in the graph summarize the price movements using intrinsic and physical time
- Significant events of trading activity are ignored when we consider changes over time based on fixed time intervals
Directional-change : definition
Terminology
Extreme point / DCC point
- If the inequality just above holds,
| Term | Description | Example in figure |
|---|---|---|
| Extreme point | the time at | points , , , , , , |
| DCC point | the time at | points , , , , , , |
- Note that whilst an extreme point is the end of the one trend, it is also the start point of the next trend
- An extreme point is only recognized in hindsight; precisely at the DCC point
DC event / OS event
- DC means "Directional Change" and OS does "Overshoot"
| Term | Description | Example in figure |
|---|---|---|
| DC event | -starts with an extreme point -ends with a DCC point | intervals , , , |
| DCC point | -starts at the DCC point -ends at the next extreme point | ntervals , , , |
- Note that for a given time series and a predetermined threshold, the DC summary is unique
Definition of DC
- A directional-change(DC) event can take one of the two forms
- a downturn event
- an upturn event
- Note that a downturn event occurs in upward run and an upturn event occurs in downward run
| downward run | upward run |
|---|---|
| A period between a downturn event and the next upturn event | A period between a upturn event and the next downturn event |
| The last low price is continuosly updated to the minimum of the current market price and the last low price | The last high price is continuosly updated to the maximum of the current market price and the last high price |
| An event is an event when the absolute price change between the current market price and the last low price is higher than a given threshold , i.e., If this holds, the point which the price last troughed ( is the starting point of a upturn event | An event is an event when the absolute price change between the current market price and the last high price is lower than a given threshold , i.e., If this holds, the point which the price last peaked ( is the starting point of a downturn event |
Implementation in Python
def myDC(data, d=0.2):
'''
- Aloud, M., Tsang, E., Olsen, R. & Dupuis, A. (2012). A Directional-Change Event Approach for Studying Financial Time Series. Economics, 6(1), 20120036.
- data : a list or array-like time series object
- d : theta value, which is a threshold to decide upturn/downturn event
'''
p = pd.DataFrame({
"Price": data
})
p["Event"] = ''
run = "upward" # initial run
ph = p['Price'][0] # highest price
pl = ph # lowest price
pl_i = ph_i = 0
for t in range(0, len(p)):
pt = p["Price"][t]
if run == "downward":
if pt < pl:
pl = pt
pl_i = t
if pt >= pl * (1 + d):
p.at[pl_i, 'Event'] = "start upturn event"
run = "upward"
ph = pt
ph_i = t
# print(">> {} - Upward! : {}%, value {}".format(pl_i, round((pt - pl)/pl, 2), round(pt - pl,2)))
elif run == "upward":
if pt > ph:
ph = pt
ph_i = t
if pt <= ph * (1 - d):
p.at[ph_i, 'Event'] = "start downturn event"
run = "downward"
pl = pt
pl_i = t
# print(">> {} - Downward! : {}%, value {}".format(ph_i, round((ph - pt)/ph, 2), round(ph - pt,2)))
return p