2.1 경험 오차 및 과적합

오차율과 정확도: 모델 성능의 기본 척도

• 오차율(Error Rate): 분류 모델이 잘못 예측한 샘플의 비율입니다. 예를 들어, 100개의 샘플 중 10개를 잘못 분류했다면 오차율은 10%입니다.
• 정확도(Accuracy): 분류 모델이 올바르게 예측한 샘플의 비율입니다. 위 예시에서 정확도는 90%가 됩니다. 정확도는 1 - 오차율로 계산할 수 있습니다.

훈련 오차와 일반화 오차: 모델의 진짜 실력

• 훈련 오차(Training Error) 또는 경험 오차(Empirical Error): 모델이 학습 데이터(Training Data)에서 보여주는 오차입니다. 즉, 모델이 이미 학습한 문제지에 대해 얼마나 좋은 점수를 받는지를 나타냅니다.
• 일반화 오차(Generalization Error): 모델이 새로운 데이터(Test Data), 즉 학습 과정에서 보지 못했던 데이터에 대해 보여주는 오차입니다. 머신러닝의 목표는 이 일반화 오차를 최소화하는 모델을 찾는 것입니다. 훈련 오차가 아무리 낮아도 일반화 오차가 높다면 그 모델은 실전에서 쓸모가 없습니다.

과적합과 과소적합: 모델 학습의 딜레마

• 과적합(Overfitting): 모델이 학습 데이터에 너무 깊게 파고들어 데이터의 특성뿐만 아니라 노이즈까지 학습해버린 상태를 말합니다. 이 경우 훈련 오차는 매우 낮지만 일반화 오차는 높게 나타납니다. 과적합은 머신러닝에서 피하기 어렵고 해결하기 까다로운 주요 문제 중 하나입니다. 마치 시험공부를 할 때 족보만 달달 외워 응용 문제를 전혀 풀지 못하는 것과 같습니다.

• 과소적합(Underfitting): 모델이 학습 데이터의 패턴을 충분히 학습하지 못한 상태입니다. 이 경우 훈련 오차와 일반화 오차 모두 높게 나타납니다. 모델이 너무 단순해서 데이터의 복잡한 관계를 파악하지 못하는 것이 원인입니다.

모델 선택: 최적의 알고리즘과 파라미터 찾기

이러한 문제들을 해결하고 일반화 성능이 가장 좋은 모델을 찾는 과정을 모델 선택(Model Selection)이라고 합니다. 모델 선택은 크게 두 가지로 나눌 수 있습니다.

• 학습 알고리즘 선택: 어떤 종류의 알고리즘(예: 결정 트리, 서포트 벡터 머신, 딥러닝 등)을 사용할지 선택하는 것입니다.
• 파라미터 선택: 선택한 알고리즘의 세부 설정을 조정하는 것입니다. 예를 들어, 결정 트리에서는 가지치기(Pruning)를 통해 과적합을 방지할 수 있고, 딥러닝에서는 에포크(Epoch) 수를 늘려 과소적합을 해결할 수 있습니다.

2.2 모델 성능 평가 방법

1. 홀드아웃 (Hold-out)

• 전체 데이터를 훈련 세트(Training Set)와 테스트 세트(Test Set), 두 개로 분리합니다.
• : 훈련 세트로 모델을 학습시킨 후, 모델이 한 번도 보지 못한 테스트 세트로 성능을 평가합니다. (보통 7:3 또는 8:2 비율로 나눕니다.)
• 단점: 데이터가 어떻게 나뉘었는지에 따라 평가 결과가 크게 달라질 수 있습니다. 예를 들어, 우연히 쉬운 데이터만 테스트 세트에 몰리면 모델 성능이 실제보다 좋게 평가될 수 있습니다.

층화 추출법 (Stratified Sampling)

• 홀드아웃의 단점을 보완하기 위한 방법입니다. 데이터의 클래스(정답) 비율을 원래 데이터셋과 동일하게 유지하면서 데이터를 나누는 방식입니다.
  • 예시: 1000개의 데이터 중 '정상'이 900개, '불량'이 100개(9:1 비율) 있다면, 7:3으로 나눌 때 훈련 세트에도 9:1 비율(정상 630, 불량 70), 테스트 세트에도 9:1 비율(정상 270, 불량 30)이 되도록 추출합니다. 이렇게 하면 데이터 쏠림 현상을 방지하여 더 안정적인 평가가 가능합니다.

2. 교차 검증 (Cross-Validation)

• 데이터를 한 번만 나누는 홀드아웃 방식의 불안정성을 개선한 방법입니다. 모든 데이터가 한 번씩은 테스트에 사용되도록 하여 더 신뢰도 높은 평가 결과를 얻습니다.

• k-폴드 교차 검증 (k-Fold Cross-Validation): 가장 널리 쓰이는 방식입니다.

• 첫 번째 폴드를 테스트 세트로 사용하고, 나머지 k-1개 폴드를 훈련 세트로 사용해 모델을 학습하고 평가합니다.

• 이번엔 두 번째 폴드를 테스트 세트로, 나머지를 훈련 세트로 사용해 평가합니다. 이 과정을 k번 반복하여 k개의 평가 점수를 얻고, 이 점수들의 평균을 최종 성능으로 삼습니다.

• 장점: 모든 데이터를 평가에 활용하므로 평가 결과가 안정적이고 신뢰도가 높습니다.

  • LOOCV (Leave-One-Out Cross-Validation)
    교차 검증의 아주 특별한 경우입니다. 데이터 샘플의 개수(n)만큼 폴드를 나누는 것(k=n) 입니다.
    과정: 전체 데이터(n개) 중 단 1개의 샘플만 테스트 세트로 사용하고, 나머지 n-1개를 훈련 세트로 사용합니다. 이 과정을 모든 샘플에 대해 한 번씩, 즉 n번 반복합니다.
    장점: 데이터셋의 편향이 거의 없는, 매우 정확한 성능 추정치를 얻을 수 있습니다.
    단점: 데이터 개수만큼 모델을 훈련해야 하므로 데이터가 조금만 커져도 계산 비용이 엄청나게 커져 현실적으로 사용하기 어렵습니다.

3. 부트스트래핑 (Bootstrapping)

• 데이터가 적을 때 유용하게 사용할 수 있는 평가 방법입니다.
  • 과정:
    전체 데이터셋(n개)에서 랜덤으로 1개의 샘플을 뽑아 새로운 데이터셋에 추가합니다. 이때 뽑았던 샘플은 다시 원래 데이터셋에 집어넣습니다. (복원)
    이 과정을 n번 반복하여 원본과 크기가 같은 새로운 부트스트랩 데이터셋을 만듭니다. (이 데이터셋에는 중복된 샘플이 포함될 수 있습니다.)
    이 부트스트랩 데이터셋을 훈련 세트로 사용합니다.
    이때 한 번도 뽑히지 않은 샘플들(약 36.8%)이 있는데, 이를 OOB(Out-of-Bag) 샘플이라고 부르며 테스트 세트로 활용합니다.

특징: 교차 검증과 달리 훈련 세트와 테스트 세트가 나뉘지 않고, 데이터의 분포를 추정하거나 모델 성능의 안정성을 확인할 때 주로 사용됩니다.

🛠️ 파라미터 튜닝과 최종 모델 선택

이제 모델을 '어떻게' 만들지 결정하는 과정입니다. 여기서 파라미터와 검증 세트의 개념이 중요합니다.

파라미터란? (Parameters)

• 모델의 파라미터는 크게 두 종류로 나뉩니다.

  • 모델 파라미터 (Model Parameters)
    정의: 모델이 훈련 데이터로부터 스스로 학습하는 값입니다.
    예시: 선형 회귀의 기울기(W)와 절편(b), 딥러닝 모델의 수많은 가중치(Weights)들.
    우리가 직접 설정하는 값이 아니라, 모델이 학습 과정에서 최적의 값을 찾아냅니다.

  • 하이퍼파라미터 (Hyperparameters)
    정의: 모델이 학습하기 전에 사용자가 직접 설정해주는 값입니다. 모델이 학습하는 방법을 제어하는 설정값이라고 생각하면 쉽습니다. '알고리즘 파라미터'라고도 부릅니다.
    예시: 학습률(Learning Rate), 결정 트리의 최대 깊이, k-폴드 교차 검증에서의 k값, k-최근접 이웃(KNN) 알고리즘의 이웃 수 k 등.
    최적의 하이퍼파라미터를 찾는 과정을 하이퍼파라미터 튜닝이라고 합니다.

검증 세트 (Validation Set)란?

• 최적의 하이퍼파라미터를 찾으려면, 여러 하이퍼파라미터 조합으로 모델을 만들어보고 어떤 조합의 성능이 가장 좋은지 평가해야 합니다. 이때 어떤 데이터로 평가해야 할까요?

  • 훈련 세트? (X): 훈련 세트로 평가하면 무조건 모델을 복잡하게 만드는 하이퍼파라미터가 좋게 평가됩니다(과적합).

  • 테스트 세트? (X): 절대 안 됩니다. 테스트 세트는 우리 모델의 최종 성적을 매기는 '수능 시험지'와 같습니다. 수능 시험지로 모의고사를 계속 보면서 공부하면, 결국 그 시험지에만 잘하는 모델이 되어 진짜 실력을 측정할 수 없게 됩니다. 이를 '테스트 세트 정보 누수(Data Leakage)' 라고 합니다.

그래서 우리는 검증 세트(Validation Set)라는 '모의고사 시험지'를 따로 만듭니다.

최종 모델 선택 과정
데이터 분리: 전체 데이터를 훈련 세트, 검증 세트, 테스트 세트 세 부분으로 나눕니다. (예: 6:2:2)

하이퍼파라미터 튜닝:
다양한 하이퍼파라미터 조합(예: 학습률 0.1, 0.01, 0.001)을 준비합니다.
각 조합에 대해 훈련 세트로 모델을 학습시키고, 검증 세트로 성능을 평가합니다.
최적 하이퍼파라미터 선택: 검증 세트에서 가장 높은 성능을 보인 하이퍼파라미터 조합을 선택합니다.

2.3 모델 성능 측정

모델 평가는 크게 회귀(값을 예측)와 분류(카테고리를 예측)로 나뉩니다.

회귀 모델의 성능 측정

평균 제곱 오차 (Mean Squared Error, MSE)
실제 정답과 모델이 예측한 값의 차이를 제곱하여 평균을 낸 값입니다. 예측값이 정답에서 얼마나 떨어져 있는지를 나타내는 가장 기본적인 지표입니다.

분류 모델의 성능 측정

분류 모델의 평가는 '그래서 뭘 잘 맞췄고, 뭘 어떻게 틀렸는가'를 세세하게 따지는 것에서 시작합니다.

1. 혼동 행렬 (Confusion Matrix): 모든 평가의 시작

이진 분류(Yes/No) 문제에서 모델의 예측 결과를 4가지 상황으로 요약한 표입니다.

2. 정밀도(Precision)와 재현율(Recall)

• 정밀도 (Precision): 모델이 "Positive"라고 예측한 것들 중에서, 실제로 Positive인 것의 비율.

  • 의미: "이 모델이 암이라고 진단하면, 얼마나 믿을만한가?"

• 재현율 (Recall): 실제 "Positive"인 것들 중에서, 모델이 Positive라고 예측해낸 것의 비율.

  • 의미: "실제 암 환자들 중에서, 모델이 얼마나 놓치지 않고 찾아냈는가?"

• 정밀도-재현율 트레이드오프 (Trade-off)
  둘은 반비례 관계를 가집니다. 모델이 Positive라고 예측하는 기준(Threshold)을 낮추면 더 많은 것을 Positive로 예측하므로 재현율은 올라가지만, 그만큼 잘못 예측(FP)하는 것도 많아져 정밀도는 떨어집니다.

3. 종합 평가 지표 및 시각화

정밀도와 재현율은 한쪽만 보기 어려우므로, 이를 종합적으로 보는 지표들이 필요합니다.

• P-R 곡선 (Precision-Recall Curve)
  모델의 예측 기준(Threshold)을 계속 바꾸면서 정밀도와 재현율이 어떻게 변하는지를 그린 그래프입니다. 곡선이 오른쪽 위(정밀도=1, 재현율=1)에 가까울수록 좋은 모델입니다.

• F1 점수 (F1 Score)
  정밀도와 재현율의 조화 평균입니다. 두 지표가 모두 중요할 때, 하나의 숫자로 모델 성능을 평가하기 위해 사용합니다.

• ROC 곡선 (Receiver Operating Characteristic Curve)
  모델의 예측 기준을 바꾸면서 재현율(TPR)과 "가짜 양성 비율(FPR)"의 관계를 그린 그래프입니다.

  • TPR (True Positive Rate): 재현율과 동일합니다.
    fracTPTP+FN

  • FPR (False Positive Rate): 실제 Negative 중에서 Positive로 잘못 예측한 비율.
    fracFPFP+TN

• AUC (Area Under the Curve)
  ROC 곡선 아래의 면적입니다. 0.5(랜덤 모델) ~ 1(완벽한 모델) 사이의 값을 가지며, AUC 값이 클수록 모델의 전반적인 성능이 좋다고 평가합니다. 모델이 Positive와 Negative 샘플을 얼마나 잘 구별하는지를 나타내는 종합적인 지표입니다.

2.4 비교 검증

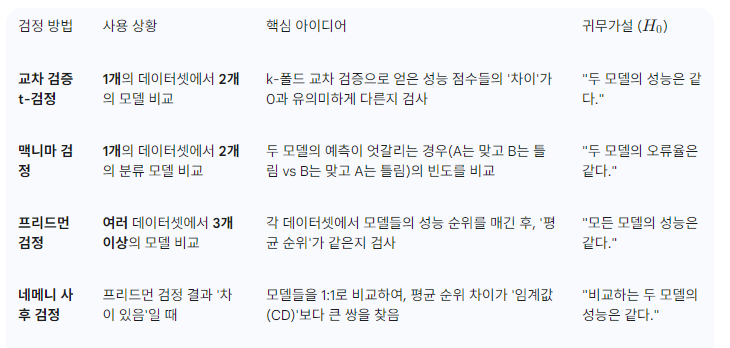
비교 검증은 모델 간의 성능 차이가 우연에 의한 것인지, 아니면 통계적으로 의미 있는 차이인지 수학적으로 확인하는 과정입니다. 모든 검정은 p-value가 기준치(보통 0.05)보다 작으면 "두 모델(들)의 성능에 유의미한 차이가 있다"고 결론 내립니다.

• 두 모델만 비교할 때: 교차 검증 t-검정이 일반적입니다. 두 모델의 예측 결과가 어떻게 다른지에 집중하고 싶다면 맥니마 검정을 사용합니다.

• 세 개 이상의 모델을 비교할 때: 먼저 프리드먼 검정을 돌려 "모델들 간에 전반적으로 성능 차이가 있는가?"를 확인합니다. 여기서 '차이가 있다'는 결론이 나오면, 네메니 사후 검정을 추가로 실시하여 구체적으로 '어떤 모델'과 '어떤 모델'이 차이가 나는지 찾아냅니다.

2.5 편향과 분산

모델의 일반화 오차(Generalization Error)는 크게 편향(Bias), 분산(Variance), 그리고 줄일 수 없는 오류(Irreducible Error) 세 가지로 분해할 수 있습니다. 이 중 편향과 분산을 이해하는 것은 모델의 과적합, 과소적합을 파악하고 제어하는 데 매우 중요합니다.

편향 (Bias)

정의: 모델이 학습 데이터에 내재된 실제 관계를 얼마나 잘 파악하는지를 나타냅니다. 편향이 높다는 것은 모델이 너무 단순해서 데이터의 복잡한 패턴을 제대로 학습하지 못하고, 예측값들이 실제 정답과 전반적으로 멀리 떨어져 있음을 의미합니다.

분산 (Variance)

정의: 훈련 데이터가 조금만 바뀌어도 모델의 예측이 얼마나 민감하게 변하는지를 나타냅니다. 분산이 높다는 것은 모델이 훈련 데이터의 특정 패턴뿐만 아니라 노이즈까지 과하게 학습하여, 새로운 데이터에 대한 예측이 매우 불안정하고 일관성이 없음을 의미합니다.

편향-분산 트레이드오프 (Bias-Variance Trade-off)

편향과 분산은 일반적으로 한쪽이 낮아지면 다른 쪽이 높아지는 상충 관계(Trade-off)에 있습니다.

• 모델이 단순해지면 (복잡도 감소):
  데이터의 미세한 변화에 덜 민감해져 분산은 감소합니다.
  하지만 데이터의 전체적인 패턴을 놓칠 가능성이 커져 편향은 증가합니다.

• 모델이 복잡해지면 (복잡도 증가):
  데이터의 복잡한 패턴을 잘 잡아내어 편향은 감소합니다.
  하지만 데이터의 노이즈까지 학습하게 되어 분산은 증가합니다.

머신러닝의 목표는 이 트레이드오프 관계를 이해하고, 총오차(Total Error) = 편향² + 분산 + 줄일 수 없는 오류를 최소화하는 최적의 모델 복잡도, 즉 "Sweet Spot"을 찾는 것입니다. 이는 과소적합과 과적합 사이의 균형을 맞추는 것과 같습니다.