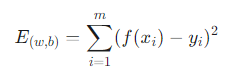3.1 선형 모델 (Linear Model)
선형 모델은 입력 데이터의 특성(feature)들에 가중치(weight)를 곱한 값들을 모두 더해 예측 결과를 만들어내는 가장 단순하고 직관적인 모델입니다. 특성과 예측 결과 사이에 직선적인 관계가 있다고 가정하죠.
ex) f잘 익은 수박(x) = 0.2색 + 0.5x꼭지모양 + 0.3x소리 +1
-
기본 식:
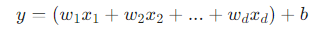
-
벡터 식:

- 비선형 모델 (Non-linear Model)
현실 세계의 복잡한 데이터는 단순한 직선 관계만으로 설명하기 어렵습니다. 비선형 모델은 이러한 복잡한 관계를 학습하기 위해 선형 모델을 기반으로 확장된 개념을 사용합니다.- 선형 모델을 여러 개 쌓거나(층) 데이터를 더 높은 차원으로 보내 비선형적인 관계를 표현할 수 있도록 만듭니다.
3.2 선형 회귀
선형 회귀의 목표와 기본 모델
선형 회귀의 목표는 데이터의 특성(feature)과 결과(target) 사이의 선형(직선) 관계를 가장 잘 나타내는 모델을 찾는 것입니다.
기본 가정: 입력 특성 x와 결과 y 사이에는 y ≈ wx + b 와 같은 직선 관계가 존재한다.
2. 비용 함수와 최소제곱법
가장 좋은 직선, 즉 최적의 w와 b를 찾기 위해, 모델의 예측값과 실제 정답의 차이인 오차(Error)를 측정하고 이를 최소화해야 합니다.
- 비용 함수 (Cost Function): 오차를 측정하는 기준으로, 회귀 문제에서는 주로 평균제곱 오차(Mean Squared Error, MSE)를 사용합니다.
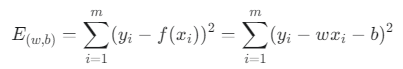
- 최소제곱법 (Least Squares Method): 위 비용 함수(오차의 제곱 합)를 최소화하는 w와 b를 찾는 방법입니다. 수학적으로는 비용 함수의 기울기가 0이 되는 지점을 찾는 것과 같습니다.
평균제곱 오차를 최소화 하는것의 기하학적 의미
- 유클리드 거리 (Euclidean distance): 우리가 흔히 아는 두 점 사이의 직선거리입니다.
- MSE 최소화: 2차원 그래프 상에 데이터 점(yᵢ)들이 흩어져 있을 때, 우리가 그린 직선(f(xᵢ) = wxᵢ + b)까지의 수직 거리들의 제곱의 합이 최소가 되는 w(기울기)와 b(y절편)를 찾는 것과 같습니다.
최적의 해 구하기 (Closed-form Solution)
E(w, b) = Σ(yᵢ - wxᵢ - b)²
w와 b의 해를 찾는 것은 위의 식을 최소화 하는 과정 입니다.
비용 함수를 각 파라미터(w, b)에 대해 편미분(partial differentiation)한 값이 0이 되는 지점을 연립방정식으로 풀면, 최적의 해를 구하는 공식을 유도할 수 있습니다. 이를 닫힌 해(closed-form solution)라고 합니다.
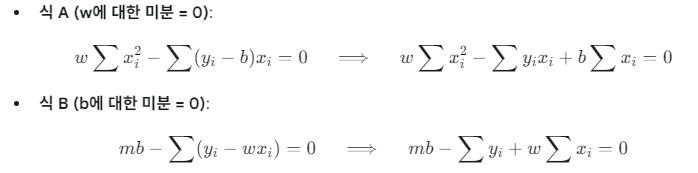
식 B를 이용해서 아래 식 구하기
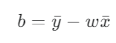

- 비용 함수를 w에 대해 편미분
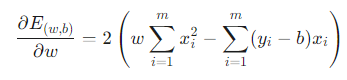
- 비용 함수를 b에 대해 편미분
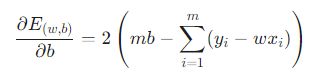
- 특성이 하나일 때:
- 최적의 기울기 w:
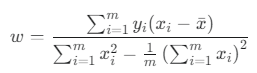
- x의 평균값
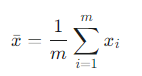
- 최적의 기울기 w:
- 최적의 편향 b:
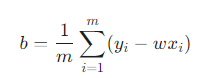
(여기서 x̄, ȳ는 각각 x와 y의 평균을 의미합니다.)
-
특성이 여러 개일 때 (다변량): 행렬을 사용하여 더 간결하게 표현하고 계산합니다.
- 최적 파라미터 벡터 ŵ (w와 b를 합친 벡터):
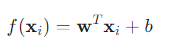
- 데이터 행렬 X
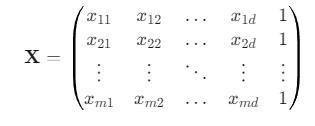
- 종속 변수 벡터 y
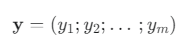
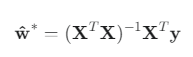
- 비용 함수의 편미분 (Gradient)
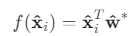
- 기울기를 0으로 설정하고 정리
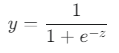
- 최정 예측 모델
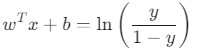
실제로 XᵀX가 풀랭크일 확률은 낮기 때문에 Regularization 필요
- 최적 파라미터 벡터 ŵ (w와 b를 합친 벡터):
-
데이터가 직선이 아니라면 단순한 선형 모델은 데이터를 잘 예측할 수 없습니다. 이 상황에서는 아래의 식을 사용합니다.(어려운 곡선 문제를 직선문제로 바꿔서 해결하는 로그-선형 회귀)
- y ≈ e^(wᵀx + b)
- ln(y) ≈ wᵀx + b
3.3 로지스틱 회귀
선형 모델을 사용하여 분류(Classification) 문제를 해결하는 대표적인 방법.
이전의 선형 회귀가 집값이나 시험 점수 같은 숫자를 예측했다면, 로지스틱 회귀는 "이 메일이 스팸일까, 아닐까?" 또는 "이 고객이 구독할까, 안 할까?"처럼 두 가지 선택지 중 하나를 결정하는 확률을 예측합니다.
-
선형 회귀의 한계
단순 선형 회귀의 예측값(wx+b)은 음의 무한대부터 양의 무한대까지 모든 숫자가 될 수 있습니다. 하지만 우리가 원하는 것은 확률, 즉 0과 1 사이의 값입니다. 선형 회귀의 결과를 확률로 해석하기는 어렵습니다. -
해결책: 시그모이드 함수 (Sigmoid Function)
이 문제를 해결하기 위해 시그모이드(Sigmoid) 함수라는 비선형 함수를 사용합니다. 이 함수는 어떤 값이든 0과 1 사이의 값으로 "찌그러뜨리는" 특징을 가집니다.
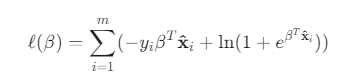
- z 자리에 선형 회귀의 예측값(wᵀx + b)이 들어갑니다.
-
로짓 변환
로짓 변환 (Logit Transformation): 식을 wᵀx + b에 대해 정리하면 다음과 같이 됩니다.
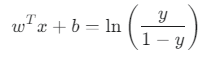
- 의미:
- y는 "성공할 확률"입니다.
- 1-y는 "실패할 확률"입니다.
- y / (1-y)는 오즈(Odds)라고 부르며, 성공 확률이 실패 확률보다 몇 배나 높은지를 나타냅
최대우도법 (Maximum Likelihood Estimation, MLE)
선형 회귀는 오차를 최소화하는 방식으로 최적의 해를 찾았습니다. 하지만 분류 문제인 로지스틱 회귀에서는 다른 접근법이 더 효과적입니다.
-
최대우도법이란?
"우리가 가진 데이터가 나타날 확률(Likelihood)을 가장 높게 만들어주는 최적의 파라미터(w, b)를 찾자"는 통계적인 방법입니다. -
ℓ(w, b) = Σ ln p(yᵢ | xᵢ; w, b)
이 식은 "모든 데이터에 대해, 모델이 실제 정답 yᵢ를 예측할 로그 확률의 총합"을 의미하며, 우리는 이 값을 최대로 만드는 w와 b를 찾고 싶습니다.
경사 하강법(Gradient Descent)
손실 함수는 볼록 함수입니다. 즉, 아래 그림처럼 밥그릇 모양이어서 최저점(Global Minimum)이 단 하나만 존재합니다. 이 최저점을 찾아가는 방법이 바로 경사 하강법입니다.
베타(β)는 가중치 벡터 w와 편향 b를 하나의 벡터로 합친 통합 파라미터 벡터입니다.
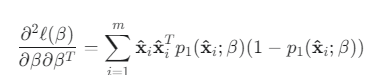
-
1차 도함수 (Gradient, 기울기)
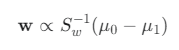
이 기울기 값을 경사 상승법(Gradient Ascent) 또는 경사 하강법(Gradient Descent)에 사용하여, β를 최적의 값으로 점진적으로 업데이트해 나갑니다. -
2차 도함수 (Hessian, 곡률)
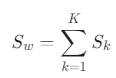
뉴턴 방법(Newton's Method)과 같은 더 발전된 최적화 알고리즘은 이 2차 도함수(곡률) 정보까지 활용하여, 단순한 경사 하강법보다 훨씬 빠르게 최적의 해를 찾아낼 수 있습니다.
3.4 선형 판별 분석(Linear Discriminant Analysis, LDA)
대표적인 분류(Classification) 알고리즘이자, 차원 축소(Dimensionality Reduction) 기법
목표: "클래스 간 분산은 최대화, 클래스 내 분산은 최소화" 하는 최적의 투영 축 w를 찾는 것
-
μ₀, μ₁ : 각 클래스(0과 1)에 속한 데이터들의 평균(중심점)
-
Σ₀, Σ₁ : 각 클래스 데이터들이 얼마나 퍼져있는지를 나타내는 공분산 행렬
-
w : 우리가 찾고 싶은 투영 축(projection axis)
-
LDA의 두 가지 목표를 하나의 식으로 합칩니다.
- 분자 (최대화 대상): 클래스 간 거리. w라는 축에 투영된 두 클래스 중심점(wᵀμ₀, wᵀμ₁) 사이의 거리입니다. 거리가 클수록 좋으므로 분자에 놓습니다.
- 분자 ≈ (wᵀμ₀ - wᵀμ₁)²
- 분모 (최소화 대상): 클래스 내 분산. w축에 투영된 각 클래스 데이터들의 퍼짐 정도(wᵀΣ₀w, wᵀΣ₁w)입니다. 퍼짐 정도가 작을수록 좋으므로 분모에 놓습니다.
- 분모 = wᵀΣ₀w + wᵀΣ₁w
클래스 내 산포 행렬, Within-class scatter matrix
- S_w = Σ₀ + Σ₁
- S_w는 모든 클래스 내부의 분산을 합친 것입니다.
클래스 간 산포 행렬, Between-class scatter matrix
-
S_b = (μ₀ - μ₁)(μ₀ - μ₁)ᵀ
-
S_b는 두 클래스 평균 사이의 거리를 나타냅니다.
-
최종 목표 함수(일반화된 레일리 몫 (Generalized Rayleigh Quotient)
- J(w) = (wᵀS_b w) / (wᵀS_w w)
라그랑주 승수법을 통한 해법
- 최대화할 함수 (f): f(w) = wᵀS_b w (클래스 간 분산)
- 제약 조건 함수 (g): g(w) = wᵀS_w w = 1 (클래스 내 분산)
라그랑주 승수법에 따르면, f(w)가 최대가 되는 지점에서는 f(w)의 기울기와 g(w)의 기울기가 평행해야 합니다.
- f(w)의 기울기: ∇f(w) = 2S_b w
- g(w)의 기울기: ∇g(w) = 2S_w w
두 벡터가 평행하다는 것은, 한 벡터가 다른 벡터의 상수배와 같다는 의미입니다. 여기서 그 상수를 λ (람다), 즉 라그랑주 승수라고 부릅니다.
- f(w)의 기울기 = λ * g(w)의 기울기
- 2S_b w = λ * (2S_w w)
- S_b w = λS_w w
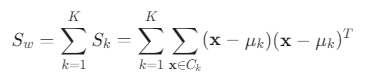
위의 식은 일단 두 클래스의 평균(중심점)을 잇는 방향 (μ₀ - μ₁)을 기본으로 하고,
각 클래스 내부의 퍼짐 정도(S_w)를 고려하여 그 방향을 보정(S_w⁻¹를 곱함)해준 것입니다.
LDA vs 로지스틱 회귀 (Logistic Regression)
-
공통점: 두 모델 모두 분류를 위한 선형 결정 경계를 만듭니다.
-
차이점: LDA는 데이터가 특정 확률 분포(가우시안 분포)를 따른다고 가정하는 생성 모델(Generative Model)인 반면, 로지스틱 회귀는 데이터의 분포를 가정하지 않고 결정 경계 자체를 찾는 판별 모델(Discriminative Model)입니다. LDA의 가정이 잘 맞으면 더 좋은 성능을 보일 수 있습니다.
다중 클래스 LDA (Multi-class LDA)
-
클래스 내 산포 행렬 S_w
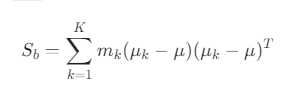
-
클래스 간 산포 행렬 S_b
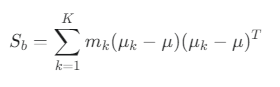
-
목표: K개의 클래스를 가장 잘 분리하는 최적의 (K-1)차원 공간을 찾습니다.
-
방법: 고유값 문제를 풀어 클래스 분리 능력이 가장 뛰어난 K-1개의 축(고유벡터)을 선택합니다.
-
결과: 분류와 차원 축소를 동시에 수행하여, 복잡한 고차원 데이터를 다루기 쉬운 저차원 데이터로 압축합니다.
3.5 다중 분류 학습
분해법과 앙상블(Ensemble)
- 분해법의 과정:
1. 하나의 다중 클래스 문제를 여러 개의 이진 분류 문제로 나눕니다.
2. 나눠진 각 문제에 대해 별도의 이진 분류기를 훈련시킵니다. (여러 명의 전문가를 만듦)
3. 새로운 데이터가 들어오면, 훈련된 모든 이진 분류기들에게 예측을 시킨 후, 그 결과를 종합하여(앙상블) 최종 결정을 내립니다.
분해 전략 (Decomposition Strategies)
1. 일대일 (One-vs-One, OvO)
N개의 클래스가 있다면, 가능한 모든 클래스 쌍(pair)에 대해 분류기를 만듭니다. 총 N(N-1)/2개의 분류기를 만듭니다.
-
예시 (A, B, C 세 클래스):
- 분류기 1: A vs B
- 분류기 2: A vs C
- 분류기 3: B vs C
-
예측: 새로운 데이터에 대해 모든 분류기들이 '투표'를 합니다. 예를 들어 분류기 1은 "A", 분류기 2는 "A", 분류기 3은 "B"라고 예측했다면, A가 2표, B가 1표를 얻어 최종 결과는 A가 됩니다.
2. 일대다 (One-vs-Rest, OvR)
N개의 클래스가 있다면, N개의 분류기를 만듭니다. 각 분류기는 "자기 클래스 vs 나머지 전부"를 구분하도록 학습합니다.
-
예시 (A, B, C 세 클래스):
- 분류기 1: A (양성) vs {B, C} (음성)
- 분류기 2: B (양성) vs {A, C} (음성)
- 분류기 3: C (양성) vs {A, B} (음성)
-
예측: 새로운 데이터에 대해 세 분류기 모두를 실행시켜, 가장 높은 확신(확률) 점수를 보인 분류기의 클래스를 최종 결과로 선택합니다.
3. 다대다 (Many-vs-Many, MvM)와 ECOC
가장 발전된 형태로, 여러 클래스를 두 개의 그룹으로 무작위로 나누어 학습시키는 방식입니다. 대표적인 예가 오류 수정 출력 코드(Error-Correcting Output Codes, ECOC)입니다.
-
핵심 아이디어: 각 클래스마다 고유한 "바코드(Codeword)"를 부여하고, 분류기들의 예측 결과를 조합하여 어떤 클래스의 바코드와 가장 비슷한지 찾는 방식입니다.
-
코딩 행렬 (Coding Matrix): 이 과정을 설계하는 표입니다.
- 행: 클래스 (A, B, C, D)
- 열: 이진 분류기 (f₁, f₂, f₃, f₄)
- 값: +1(양성 클래스로 사용), -1(음성 클래스로 사용), 0(이 학습에는 불참)

3.6 클래스 불균형 문제
한 클래스의 데이터는 엄청나게 많은데, 다른 클래스의 데이터는 극소수인 경우를 말합니다.
-
예시: 신용카드 사기 탐지 (99.9% 정상 거래 vs 0.1% 사기 거래), 희귀병 진단, 공장 불량품 검출 등.
-
문제점: 이런 데이터로 모델을 학습시키면, 모델은 정확도를 높이기 위해 그냥 다수 클래스(정상)라고만 예측하는 "게으른" 모델이 되기 쉽습니다. 정작 중요한 소수 클래스(사기)는 거의 탐지하지 못하게 됩니다.
1. 언더샘플링 (Undersampling)
방법: 다수 클래스의 데이터 수를 줄여서 소수 클래스의 수와 비슷하게 맞추는 방법입니다. 예를 들어 정상 거래 10,000개, 사기 거래 100개가 있다면, 정상 거래 데이터 중 100개만 무작위로 뽑아서 100:100으로 균형을 맞춥니다.
단점: 다수 클래스의 데이터가 대량으로 버려지므로, 중요한 정보가 손실될 수 있습니다.
언더샘플링 + 앙상블: 정보 손실을 줄이기 위해, 다수 클래스에서 여러 번 다르게 샘플링하여 여러 개의 균형 잡힌 데이터셋을 만듭니다. 그리고 각 데이터셋으로 별도의 모델을 학습시킨 후, 그 모델들의 예측을 종합(앙상블)하는 방식을 사용합니다.
2. 오버샘플링 (Oversampling)
방법: 소수 클래스의 데이터 수를 늘려서 다수 클래스의 수와 비슷하게 맞추는 방법입니다.
단순한 방법: 소수 클래스의 데이터를 그대로 복제하여 수를 늘립니다. (단점: 과적합 위험)
SMOTE (Synthetic Minority Over-sampling Technique): 단순 복제를 개선한 기법입니다. 소수 클래스의 데이터들 사이의 공간에 가상의 새로운 데이터(Synthetic Data)를 생성하여 데이터 수를 늘립니다.
원리: 소수 클래스 데이터 A와 그 주변의 가까운 데이터 B를 선택한 후, A와 B를 잇는 선 위의 어딘가에 새로운 점 C를 생성합니다.
장점: 단순 복제보다 과적합 위험이 적고, 모델이 더 일반화된 패턴을 학습하도록 돕습니다.
3. 임계값 이동 (Threshold Moving)
방법: 데이터 자체는 건드리지 않고, 모델의 "판단 기준"을 바꾸는 방법입니다.
원리: 로지스틱 회귀는 보통 예측 확률이 50%(임계값 0.5)를 넘으면 양성(Positive)으로 판단합니다. 하지만 불균형 데이터에서는 소수 클래스의 예측 확률이 낮게 나오는 경향이 있습니다.
해결책: 이 임계값을 0.5에서 0.2나 0.1처럼 대폭 낮춥니다. 이제 모델이 "사기일 확률이 20%만 돼도 일단 사기라고 의심해!"라고 더 민감하게 판단하도록 기준을 바꾸는 것입니다.