" 신경망이란, 적응성이 있는 단순 단위로 구성된 광범위하고 서로 연결된 네트워크다. 이 조직은 현실 세계 사물에 대한 생물 신경계통의 상호작용을 모방할 수 있다."

5.1 뉴런 모델

McCulloch and pitts neuron

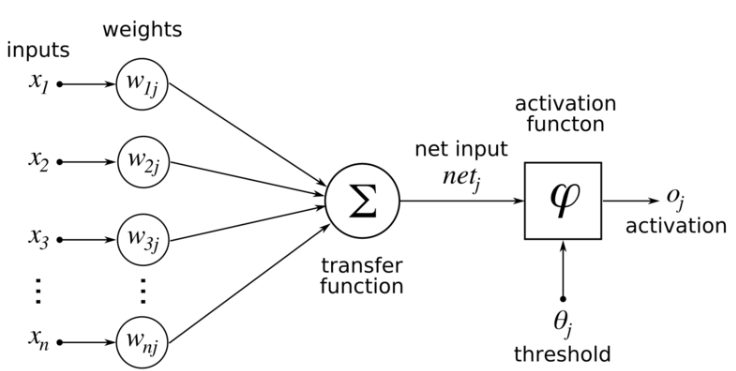
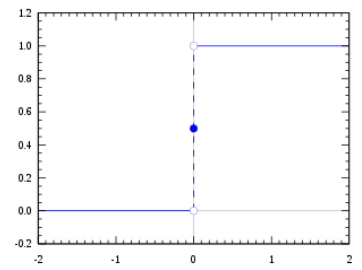
• 가장 이상적인 활성화 함수
  
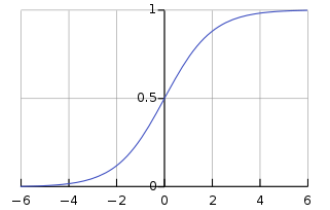
• 불연속성이라는 특성을 보안한 함수(sigmoid function == Squasing function)
  

5.2 퍼셉트론과 다층 네트워크

Perceptron

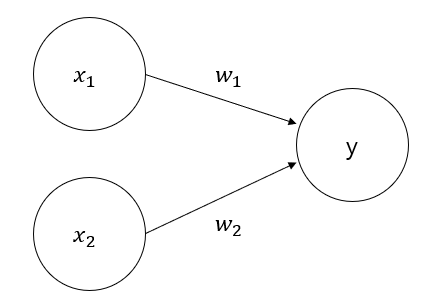
두 개의 뉴런으로 구성되어 입력층이 외부 입력 신호를 받은 후 출력층으로 전달하는 구조
출력층은 M-P neuron으로 구성

단층 퍼셉트론 (Single-Layer Perceptron)

단층 퍼셉트론은 AND, OR, NAND와 같은 논리 연산을 계산할 수 있는 신경망의 가장 기본적인 형태입니다. 그 구조는 다음과 같은 수식으로 표현됩니다.

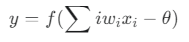
• 학습 과정:

  • 퍼셉트론은 훈련 데이터를 통해 가중치(w)와 임계값(θ)을 학습합니다.
    
    만약 퍼셉트론의 예측(y^)이 실제 값(y)과 일치하면 가중치에 변화가 없고, 예측이 틀리면 가중치가 조정됩니다.

• 한계:
  단층 퍼셉트론은 선형적으로 분리가 가능한 문제만 해결할 수 있습니다. 예를 들어 XOR 문제와 같이 선형적으로 분리할 수 없는 문제는 해결할 수 없습니다. 이는 단층 퍼셉트론이 오직 하나의 층(입력층과 출력층)만으로 구성되어 있기 때문이며, 이로 인해 학습 능력이 매우 제한적입니다.

다층 순방향 신경망 (Multi-Layer Feedforward Neural Networks)

단층 퍼셉트론의 한계를 극복하기 위해 제안된 구조가 다층 순방향 신경망입니다. 이는 여러 층의 뉴런을 겹겹이 쌓은 구조입니다.

• 구조적 특징:
  • 겹층 구조: 입력층, 하나 이상의 은닉층(Hidden Layer), 그리고 출력층으로 구성됩니다.
  • 순방향 연결: 각 층의 뉴런은 다음 층의 뉴런과만 연결됩니다. 같은 층의 뉴런끼리는 연결되어 있지 않으며, 층을 뛰어넘는 연결도 없습니다.
  • 기능성 뉴런: 입력층은 단순히 외부 입력을 받는 역할만 하며, 실제 신호 처리와 학습은 은닉층과 출력층의 기능성 뉴런들이 담당합니다.
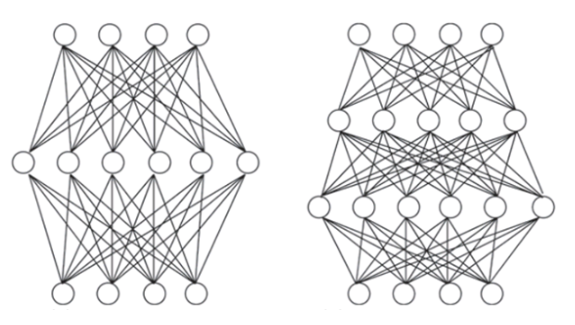
  • 단일 은닉층 신경망: 은닉층이 하나만 있는 구조를 'Neural Networks with a Single Hidden Layer'라고 부릅니다.

다중 은닉층 신경망: 두 개 이상의 은닉층을 가진 구조도 가능하며, 이는 더 복잡한 문제 해결에 사용됩니다.

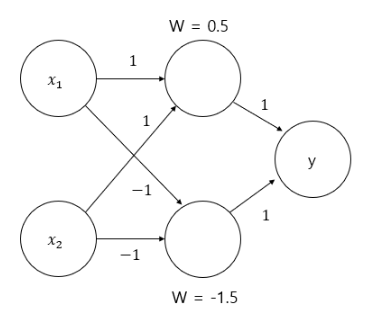
• 학습 과정:
  • 다층 순방향 신경망은 훈련 데이터를 통해 학습을 진행합니다. 학습의 핵심은 뉴런 간의 연결 가중치(w)와 각 기능성 뉴런의 임계값(θ)을 조절하는 것입니다. 즉, 신경망의 학습 능력은 이 가중치와 임계값에 내재되어 있습니다.
    

5.3 오차 역전파 알고리즘

역전파 알고리즘은 Input과 Output을 알고 있는 상태에서 신경망을 학습시키는 방법입니다. 역전파 알고리즘을 적용하기 이전에 MLP에 대해 다음과 같이 정의합니다.

• 초기 가중치 값은 랜덤으로 주어짐
• 각각의 노드는 하나의 퍼셉트론으로 생각함. 즉 노드를 지나칠 때마다 활성 함수를 적용하며, 활성화 함수를 적용하기 이전을 net, 이후를 out이라 함.
• 다음 레이어의 계산에는 out값을 사용하며, 마지막 out이 output이 됨.
• 활성화 함수로 시그모이드 함수를 사용함.

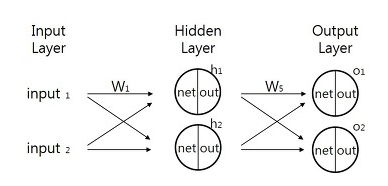
1. 기본 원리: 경사 하강법 (Gradient Descent)

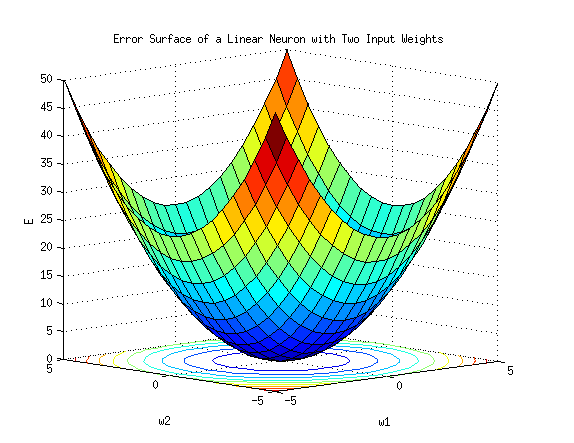
각각 가중치가 2개일때 (w1,w2), 오차 E를 도식화하면 위와 같은데, y=0,w1=0,w2=0일 때 E가 최소화됩니다.

따라서 오차 E를 모든 가중치들에 대한 방정식으로 본다면, 우리가 해야할 것은 가중치 w를 수정해 E가 최소가 되도록 만드는 것이며, 이를 위해 경사하강법(Graident Descent)라는 최적화 알고리즘을 사용합니다. 그 기본 원리는 기울기가 낮은 쪽으로 연속적으로 이속시켜 값이 최소가 되는 점인 극값에 다다르게 하는 것이라고 볼 수 있습니다.

이를 위해 오차 E를 미분하는 과정이 필요한데, 모든 가중치가 오차에 영향을 미치고 있으므로 E를 각각의 가중치로 편미분해야 합니다. 다층 신경망은 각 계층이 연결되어 있어 Output에 가까운 미분 과정에서 사용되는 값이 Output에서 먼쪽의 미분과정에 사용됩니다. 따라서 Output과 가까운 쪽의 미분을 먼저 진행하게 되며 그렇기 때문에 Back Propagation이라고 불립니다.

• 오차 함수
  

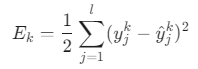
  • 의미: k번째 데이터에 대한 모델의 예측값(ŷ)과 실제 정답(y) 사이의 차이(오차)를 측정합니다. 이 오차 E_k를 최소화하는 것이 목표입니다.

• 가중치 업데이트 규칙
  

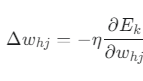
  • Δw_hj: 가중치 w_hj를 얼마나 변경할지를 나타내는 업데이트 양

  • η (에타): 학습률(learning rate). 얼마나 큰 폭으로 가중치를 수정할지 결정하는 값.

  • ∂E_k / ∂w_hj: 오차 함수 E_k를 가중치 w_hj에 대해 편미분한 값. 즉, "이 가중치를 조금 바꿨을 때 최종 오차가 얼마나 변하는가?"를 나타내는 기울기입니다.

  • 의미: 오차를 줄이는 방향(기울기의 반대 방향, -)으로 학습률(η)만큼 가중치를 업데이트하라는 뜻입니다.

2. 출력층(Output Layer) 가중치 업데이트

출력층 뉴런 j와 은닉층 뉴런 h를 연결하는 가중치 w_hj를 업데이트하는 공식입니다.

• 기울기 계산
  

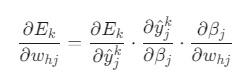
  • 의미: w_hj가 변하면 → 은닉층의 출력(β_j)이 변하고 → 최종 예측값(ŷ)이 변하고 → 최종 오차(E_k)가 변하는 과정을 연쇄적으로 미분한 것입니다.

  • 우리는 w_hj(은닉층 h → 출력층 j 가중치)가 최종 오차 E_k에 미치는 영향을 알고 싶습니다. 하지만 둘은 직접 연결되어 있지 않아 한 번에 계산할 수 없습니다. 그래서 연쇄 법칙(Chain Rule)을 이용해 중간 단계들을 연결하여 계산하는 것입니다.

  • ∂βⱼ / ∂w_hj: 가중치 w_hj가 변하면 → 출력 뉴런 j의 입력 합 βⱼ는 얼마나 변할까?

    • βⱼ는 은닉층의 출력 b_h와 가중치 w_hj의 곱(w_hj * b_h)을 포함하므로, 이 미분값은 b_h가 됩니다.

  • ∂ŷⱼᵏ / ∂βⱼ: 입력 합 βⱼ가 변하면 → 최종 예측값 ŷⱼᵏ는 얼마나 변할까?

    • 이는 활성화 함수(시그모이드)의 미분입니다. f'(z) = f(z)(1-f(z)) 이므로, 이 값은 ŷⱼᵏ(1-ŷⱼᵏ)가 됩니다.

  • ∂Eₖ / ∂ŷⱼᵏ: 예측값 ŷⱼᵏ이 변하면 → 최종 오차 Eₖ는 얼마나 변할까?

    • 오차 함수 Eₖ = ½(yⱼᵏ - ŷⱼᵏ)²를 ŷⱼᵏ에 대해 미분하면 -(yⱼᵏ - ŷⱼᵏ)가 됩니다.

• 출력층의 오차항
  위의 연쇄 법칙 중, 오차에 직접적으로 관련된 뒷부분 두 개를 곱해서 정리한 것입니다.
  

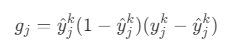
  • (yⱼᵏ - ŷⱼᵏ): 실제 정답과 예측값의 차이. 즉, 얼마나 틀렸는가?

  • ŷⱼᵏ(1-ŷⱼᵏ): 시그모이드 미분값. 예측이 0.5에 가까울수록(가장 애매한 지점) 미분값이 커집니다. 즉, 뉴런이 얼마나 변화에 민감한 상태인가?

  • 최종 가중치 업데이트
    

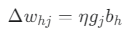
    • 의미: 은닉층 h의 출력값(b_h)이 클수록, 그리고 출력층 j의 오차(g_j)가 클수록 가중치 w_hj를 더 많이 수정하라는 뜻입니다.

3. 은닉층(Hidden Layer) 가중치 업데이트

이것이 바로 오차의 역전파입니다. 은닉 뉴런 h의 오차 eₕ는 자신이 신호를 보냈던 모든 출력 뉴런들의 오차(gⱼ)를 다시 돌려받아 계산합니다.

• 오차항 계산
  

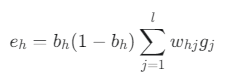
1. Σ w_hj g_j: 뉴런 h와 연결된 모든 출력 뉴런 j들로부터 각각의 오차(gⱼ)를 연결 가중치(w_hj)만큼 곱해서 전달받아 모두 더합니다. 이것이 바로 출력층의 오차(g)가 은닉층으로 거꾸로 전파(w_hj를 타고)되는 과정입니다.

2. bₕ(1-bₕ): 은닉 뉴런 h 자신이 얼마나 변화에 민감한 상태인지(시그모이드 미분값)를 곱해줍니다.

Pseudo Code

for training_repeat
  for training_sets

		// 가중치로 net, out 계산 
		forward pass              

		//output 레이어에서 시작해 input + 1 레이어로
		for i = output layer -> i = input layer + 1     
			for all nodes in layer i
				set delta
			
			//layer i와 i-1 사이에 있는 가중치 갱신
		  	for all weights between layer i and layer i-1  
				update weight    

5.4 글로벌 미니멈과 로컬 미니멈

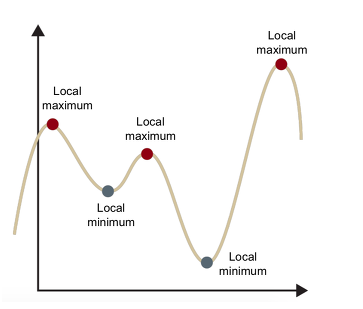
로컬 미니멈 문제란?

경사 하강법은 마치 눈을 가리고 산을 내려가는 것과 같습니다. 현재 위치에서 경사가 가장 낮은 방향으로 한 걸음씩 내려가다 보면 어느새 계곡의 가장 낮은 지점에 도착하게 됩니다.

문제는, 내가 도착한 계곡(로컬 미니멈)이 이 산 전체에서 가장 낮은 지점(글로벌 미니멈)이라는 보장이 없다는 것입니다. 더 깊은 계곡이 옆에 있는데도, 일단 한 계곡의 바닥에 도착하면 경사가 0이 되어 움직임을 멈추게 됩니다. 이것이 바로 '로컬 미니멈 함정'입니다.

• 담금질 기법 (Simulated Annealing)
  • 확률적으로 나쁜 선택(오르막)을 허용하여 현재의 계곡을 탈출
• 확률적 경사 하강법 (SGD)
  • 기울기 계산에 노이즈를 추가하여 비틀거리며 함정에서 탈출

5.5 기타 신경망

RBF (Radial Basis Function) 신경망

• "중심점(Center)으로부터의 거리가 가까울수록 크게 활성화된다"는 개념을 이용하는 신경망입니다. 주로 함수 근사(function approximation)나 분류 문제에 사용됩니다.

• 작동 원리:
  1. 은닉층(Hidden Layer): 각 뉴런이 하나의 '중심점' 또는 '프로토타입' 데이터 포인트를 가집니다. 활성화 함수로 가우시안 함수(종 모양 곡선) 같은 방사 기저 함수(RBF)를 사용합니다. 입력 데이터가 특정 뉴런의 중심점과 가까우면 해당 뉴런은 강하게 활성화(높은 값 출력)되고, 멀어지면 약하게 활성화됩니다.
  2. 출력층(Output Layer): 은닉층 뉴런들의 활성화 값들을 선형적으로 조합하여 최종 결과를 예측합니다.
  

ART (Adaptive Resonance Theory) 신경망

• "새로운 것을 배우면서 기존의 지식을 잊지 않는" 인간의 학습 방식을 모방한 비지도 학습(Unsupervised Learning) 클러스터링 알고리즘입니다.

• 작동 원리:
  1. 입력 데이터가 들어오면, 기존에 생성된 클러스터(뉴런)들과의 유사도를 비교합니다.

  	2. 만약 특정 클러스터와 충분히 유사하다면(설정된 경계 파라미터(Vigilance Parameter) 기준을 넘으면), 해당 클러스터에 데이터를 포함시키고 클러스터 정보를 업데이트합니다.
  	3. 만약 어떤 기존 클러스터와도 충분히 유사하지 않다면, 새로운 클러스터를 생성하여 데이터를 할당합니다.

SOM (Self-Organizing Map) 신경망

• 고차원의 데이터를 저차원(주로 2차원)의 격자(Grid) 위에 지도를 만들 듯 시각화하는 비지도 학습 알고리즘입니다.

• 작동 원리:
  1. 입력 데이터와 가장 유사한 가중치를 가진 뉴런(노드)을 2차원 격자 위에서 찾습니다. 이 뉴런을 BMU(Best Matching Unit)라고 합니다.
  2. BMU의 가중치를 입력 데이터와 더 비슷해지도록 업데이트합니다.
  3. 가장 중요한 특징으로, BMU뿐만 아니라 그 주변의 이웃 뉴런들도 함께, 하지만 더 약한 강도로 업데이트합니다.
  

중첩된 상호연관 신경망 (Hopfield Network)

• 연관 메모리(Associative Memory)처럼 동작하는 순환 신경망(RNN)의 한 종류입니다. 뇌가 불완전한 정보로부터 전체 정보를 기억해내는 방식을 모방합니다.

• 작동 원리:
  1. 모든 뉴런이 다른 모든 뉴런과 상호 연결된 구조를 가집니다.
  2. 네트워크에 특정 패턴(메모리)들을 저장하면, 이는 네트워크의 안정된 상태(에너지 함수의 최저점)가 됩니다.
  3. 노이즈가 섞이거나 일부가 손상된 불완전한 패턴을 입력으로 주면, 뉴런들의 상태가 상호작용을 통해 동적으로 변하다가 가장 가까운(유사한) 원본 메모리 상태로 수렴합니다.
  

엘만 네트워크 (Elman Network)

• 순환 신경망(RNN)의 초기 형태로, 단기 기억을 통해 순서가 있는 데이터를 처리합니다.

• 작동 원리:
  1. 기본적인 다층 퍼셉트론 구조에 특별한 연결이 추가됩니다.
  2. 은닉층의 이전 타임스텝(t-1)에서의 출력값을 컨텍스트 유닛(Context Unit)이라는 곳에 복사해 두었다가, 다음 타임스텝(t)에서 입력 데이터와 함께 은닉층의 입력으로 다시 사용합니다.
  3. 이 피드백 루프를 통해 네트워크는 바로 직전의 상태를 기억하고 현재의 예측에 반영할 수 있습니다.
  

볼츠만 머신 (Boltzmann Machine)

• 통계 물리학의 개념을 도입한 확률적인(Stochastic) 생성 모델입니다. 네트워크의 상태가 확률적으로 결정됩니다.

• 작동 원리:
  1. 뉴런들이 '켜짐(1)' 또는 '꺼짐(0)' 상태를 확률적으로 가집니다.
  2. 네트워크의 전체 상태에 대한 '에너지' 함수를 정의하고, 에너지가 낮을수록 해당 상태가 나타날 확률이 높도록 설계됩니다.
  3. 학습을 통해 데이터의 확률 분포 자체를 학습하려고 시도합니다

추가

• RNN은 시퀀스의 각 요소를 처리할 때마다, 예측 결과와 함께 은닉 상태(Hidden State)라는 '메모리'를 출력합니다. 이 은닉 상태는 다음 요소가 입력될 때, 새로운 입력 데이터와 함께 다시 네트워크로 들어가 현재까지의 문맥 정보를 전달하는 역할을 합니다.

5.6 딥러닝

DBN (Deep Belief Network, 심층 신뢰 신경망)

"깊은 신경망을 어떻게 똑똑하게 초기화할까?" 라는 문제를 해결한, 딥러닝 초기의 획기적인 모델입니다.

• 핵심 아이디어: 전체 신경망을 한 번에 학습시키지 않고, 한 층씩 차근차근, 정답 없이(비지도 학습) 미리 훈련시켜 가중치를 좋은 출발점에 놓는 것입니다.

• 구조: 제한된 볼츠만 머신(RBM)을 여러 개 쌓아 올린 형태입니다.

• 학습 과정 (2단계):

  1. 사전학습 (Pre-training): RBM을 한 층씩 쌓아 올리며 데이터의 저수준 특징부터 고수준 특징까지 비지도 방식으로 학습합니다. 이 과정을 통해 가중치들이 데이터의 구조를 이미 잘 파악한 "똑똑한" 초기값을 갖게 됩니다.

  2. 파인튜닝 (Fine-tuning): 사전학습이 끝난 전체 네트워크의 맨 위에 출력층을 추가하고, 정답이 있는 데이터(지도 학습)와 역전파 알고리즘을 이용해 전체 가중치를 목표에 맞게 미세 조정합니다.

'비지도 사전학습 + 지도 파인튜닝' 전략을 통해, 과거의 가장 큰 난제였던 기울기 소실(Vanishing Gradient) 문제를 해결하고 깊은 신경망의 학습을 가능하게 한 역사적으로 매우 중요한 모델입니다.

RNN (Recurrent Neural Network, 순환 신경망)

"순서가 있는 데이터" (예: 문장, 시계열 데이터)를 처리하기 위해 설계된, '기억'을 가진 신경망입니다.

• 핵심 아이디어: 네트워크 내부에 순환하는 루프(Loop)를 만들어, 이전 단계의 정보를 현재 단계의 예측에 반영합니다.

• 구조: 각 시점의 예측 결과를 계산할 때, 현재의 입력 데이터뿐만 아니라 이전 시점의 정보를 요약한 은닉 상태(Hidden State)를 함께 입력으로 사용합니다. 이 은닉 상태가 바로 RNN의 '메모리' 역할을 합니다.

• 작동 방식:
  1. 첫 번째 단어(입력)를 처리하고 결과와 함께 첫 번째 기억(은닉 상태)을 만듭니다.
  2. 두 번째 단어를 처리할 때는, 두 번째 단어와 첫 번째 기억을 함께 고려하여 결과와 두 번째 기억을 만듭니다.
  3. 이 과정을 시퀀스의 끝까지 반복하며, 과거의 정보를 계속 누적하여 현재의 예측에 활용합니다.

'메모리(은닉 상태)'를 통해 과거의 정보를 현재로 전달하는 순환 구조를 가진 신경망으로, 문장 번역, 음성 인식 등 순차적인 데이터를 다루는 데 필수적입니다. (단, 긴 시퀀스의 기억을 잘 못하는 단점이 있어 이를 보완한 LSTM, GRU가 널리 쓰입니다.)

CNN (Convolutional Neural Network, 합성곱 신경망)

이미지 인식에 혁명을 가져온, '가중치 공유' 개념을 사용하는 시각 정보 처리에 특화된 신경망입니다.

• 핵심 아이디어: 이미지의 특정 패턴(예: 고양이 귀)은 이미지의 어느 위치에 있든 같은 방법으로 찾을 수 있다는 점에 착안, 하나의 필터(Filter)를 이미지 전체에 공유하여 사용합니다.

• 구조: [합성곱 계층 → 풀링 계층] 구조를 여러 겹으로 쌓아 만듭니다.

  • 합성곱(Convolution) 계층: 특정 패턴(선, 모서리, 질감 등)을 감지하는 작은 필터(커널)가 이미지 위를 훑고 지나가며 특성 맵(Feature Map)을 만듭니다. 이 필터의 가중치가 이미지 전체에서 공유됩니다.

  • 풀링(Pooling) 계층: 특성 맵의 크기를 줄여(Downsampling) 계산량을 줄이고, 위치 변화에 좀 더 둔감한(강건한) 특징을 추출합니다.

• 작동 방식: 초기 계층에서는 선이나 모서리 같은 단순한 특징을, 깊은 계층으로 갈수록 눈, 코, 입과 같은 더 복잡하고 추상적인 특징을 학습하여 최종적으로 이미지를 분류합니다.

'필터(커널)'를 이미지 전체에 공유(가중치 공유)하여, 위치에 상관없이 효율적으로 시각적 패턴을 찾아내는 신경망입니다. 파라미터 수를 획기적으로 줄이면서 이미지 인식 성능을 극대화했습니다.