4.1 기본 프로세스

의사결정 트리 기본 알고리즘

입력:

• 훈련 세트 D = {(x₁, y₁), (x₂, y₂), ..., (xₘ, yₘ)};
• 속성 집합 A = {a₁, a₂, ..., a_d}

과정:
함수 TreeGenerate(D, A)
1: node를 생성;

2: if D의 샘플이 모두 클래스 C에 속할 경우 then => 완벽히 분류

  3: node를 C 클래스의 단말 노드로 표기 후 return;

4: end if

5: if A = ∅ OR D의 샘플이 A에서 동일할 경우 then

  6: node를 터미널 노드로 표기하고, 해당 클래스를 D에서 샘플 중 수가 가장 많은 클래스로 표기 후 return; => 더이상 나눌 수 없는경우

7: end if

8: A에서 최적의 분할 속성 a*를 선택; => 최적의 속성 선택

9: for a의 매 값 aᵛ do

 10: node를 위해 하나의 가지를 생성; D에서 a의 속성값이 aᵛ인 샘플을 D_v라 할 때

 11: if D_v = 0 then

  12: 가지를 단말 노드로 표기하고, 클래스를 D에서 샘플 수가 가장 많은 클래스로 표기

 13: else

  14: TreeGenerate(D_v, A \ {a*})가 반환한 노드로 가지를 표기

 15: end if

16: end for

알고리즘 설명

이 알고리즘은 재귀(Recursion)를 이용해 의사결정 트리를 만드는 과정을 설명합니다. "데이터를 가장 잘 나눌 수 있는 질문은 무엇인가?"를 반복적으로 찾아가며 나무를 성장시키는 분할 정복(Divide and Conquer) 전략을 사용합니다.

1. 재귀의 종료 조건: 나무가 성장을 멈추는 경우

더 이상 데이터를 나누지 않고, 현재 노드를 최종 결정(답변)을 내리는 단말 노드(Leaf Node)로 만드는 세 가지 조건이 있습니다.

• 조건 1 (완벽하게 분류됨): 현재 노드에 모인 데이터들이 모두 같은 클래스일 때. 이미 분류가 끝났으므로 더 이상 질문할 필요가 없습니다.

• 조건 2 (더 이상 나눌 수 없음): 질문할 속성이 다 떨어졌거나, 남은 데이터들의 속성값이 모두 똑같아 나눌 기준이 없을 때. 어쩔 수 없이 멈추고, 현재 모인 데이터 중 가장 많은 쪽(다수결)을 예측 결과로 정합니다.

• 조건 3 (분할 후 데이터 없음): 최적의 속성으로 데이터를 나눴는데, 특정 가지에 해당하는 데이터가 하나도 없을 때. 이 경우에도 나누기 전 데이터의 다수결을 따라 예측 결과를 정합니다.

2. 재귀 단계: 나무가 자라는 과정

위의 멈춤 조건에 해당하지 않으면, 다음과 같이 데이터를 나누어 트리를 성장시킵니다.

• 최적의 속성 선택 (가장 중요한 단계): 현재 데이터 그룹을 가장 잘 나눌 수 있는 하나의 질문(최적의 분할 속성 a*)을 선택합니다. 예를 들어 '색상', '모양', '크기' 중 '색상'으로 나누는 것이 가장 효과적이라고 판단하는 것입니다.

• 데이터 분할 및 재귀 호출:
  1. 선택된 속성('색상')의 각 값('빨강', '파랑' 등)에 대해 새로운 가지를 만듭니다.
  2. '빨강' 가지에는 빨간색 데이터들만 모으고, '파랑' 가지에는 파란색 데이터들만 모읍니다.
  3.나누어진 각 데이터 그룹에 대해, 다시 TreeGenerate 함수를 호출하여 이 과정을 처음부터 반복합니다.

4.2 분할 선택

4.2.1 정보 이득

1. 정보 엔트로피 (Information Entropy) - 불순도 측정하기

먼저 데이터가 얼마나 "지저분하게" 섞여 있는지, 즉 불순도(impurity) 또는 불확실성(uncertainty)을 측정해야 합니다. 이 측정 도구가 바로 정보 엔트로피입니다.

• 엔트로피가 높다: 여러 클래스가 비슷하게 섞여 있어 예측하기 어렵다 (불순도 높음). (예: 예/아니오가 50:50으로 섞인 경우)
• 엔트로피가 낮다: 한쪽 클래스가 대부분이라 예측하기 쉽다 (순도 높음). (예: 99%가 '예'인 경우)

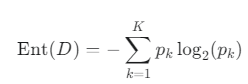
2. 정보 이득 (Information Gain) - 어떤 질문이 가장 좋은가?

정보 이득은 특정 속성(질문)으로 데이터를 나누었을 때, 엔트로피(불순도)가 얼마나 많이 줄어들었는지를 나타내는 값입니다. 당연히 정보 이득이 가장 큰 속성이 가장 좋은 질문(분할 기준)이 됩니다.

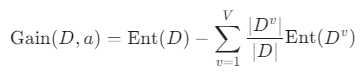
3. 최적의 분할 속성 a* 선택

의사결정 트리 알고리즘 8단계의 최적의 분할 속성 a를 선택하는 과정은 바로 이 정보 이득을 이용합니다.

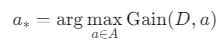
이 식은 "모든 속성 a에 대해 정보 이득 Gain(D, a)을 각각 계산하고, 그 값이 최대(max)가 되게 하는 속성 a를 a로 선택하라"는 의미입니다.

4.2.2 정보 이득율

1. 정보 이득의 문제점

정보 이득은 값(종류)이 많은 속성을 편애하는 경향이 있습니다.

예를 들어 '학번'이라는 속성이 있다고 해봅시다. 학생마다 학번이 다르므로, 이 속성으로 데이터를 나누면 모든 그룹의 순도가 100%가 되어 정보 이득이 매우 높게 계산됩니다. 하지만 '학번'은 전혀 유용한 분류 기준이 아닙니다.

2. 해결책: 정보 이득률 (Gain Ratio)

정보 이득률은 이러한 편향을 바로잡기 위해 패널티를 도입합니다.

고유값 (Intrinsic Value, IV(a))

이 패널티의 역할을 하는 것이 바로 고유값(IV)입니다. 고유값은 속성 자체가 얼마나 다양한 값을 갖는지, 즉 속성의 "복잡성"을 측정합니다.

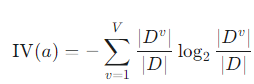
• 이 식은 정보 엔트로피 식과 형태가 똑같습니다. 단지 클래스 비율 대신, 속성값의 비율을 사용합니다.
• 속성값의 종류가 많을수록 (예: '학번'), 고유값(IV)은 커집니다.
• 속성값의 종류가 적을수록 (예: '성별'), 고유값(IV)은 작아집니다.

정보 이득률 (Gain Ratio) 공식

정보 이득률은 정보 이득을 이 고유값으로 나누어 계산합니다.

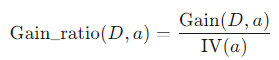
• 작동 원리: '학번'처럼 값의 종류가 많은 속성은 정보 이득(Gain)이 높게 나오더라도, 패널티인 고유값(IV) 역시 매우 커집니다. 결국 분모가 커져서 전체 정보 이득률(Gain Ratio) 값은 낮아지게 됩니다.

4.2.3 지니계수

지니 계수(Gini Index)는 데이터의 불순도(Impurity)를 측정하는 지표로, CART 의사결정 트리에서 분할 속성을 선택하는 기준으로 사용됩니다.

지니 계수는 "데이터 집합에서 무작위로 두 개의 샘플을 뽑았을 때, 두 샘플이 서로 다른 클래스에 속할 확률"을 의미합니다. 이 값이 낮을수록 데이터의 순도가 높다고 판단합니다.

지니 값 (Gini Value)

한 데이터 집합 D의 불순도를 계산하는 식입니다.

Gini(D) 공식

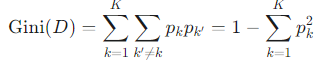
"1 - (같은 클래스를 두 번 연속 뽑을 확률)"을 의미하며, 이것이 바로 "다른 클래스를 뽑을 확률"이 됩니다.

지니 지수 (Gini Index)

속성 a로 데이터를 분할했을 때의 불순도를 나타내는 지표입니다. 정보 이득과 달리, 지니 지수는 가장 작은 값을 갖는 속성을 최적의 분할 기준으로 선택합니다.

Gini_index(D, a) 공식

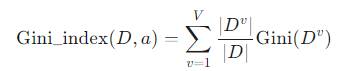
4.3 가지치기 (Pruning): 과적합 방지 전략

의사결정 트리를 아무런 제한 없이 끝까지 성장시키면, 훈련 데이터의 아주 사소한 특징이나 노이즈까지 모두 학습하여 과적합이 발생합니다. 이는 새로운 데이터에 대한 예측 성능을 떨어뜨립니다.

가지치기는 이렇게 불필요하게 복잡해진 나무의 가지를 잘라내어 모델을 더 단순하고 일반적인 형태로 만드는 과정입니다. 마치 정원사가 무성한 나뭇가지를 쳐내어 나무를 더 건강하게 만드는 것과 같습니다.

1. 사전 가지치기 (Pre-pruning)

• 개념: 나무가 완전히 성장하기 전에, 특정 조건에 도달하면 성장을 미리 멈추는 방식입니다.

• 동작 방식: 트리의 노드를 분할하기 전에, 분할의 이득을 평가합니다.

  • 예를 들어, 현재 노드를 분할했을 때 검증 세트(Validation Set)에서의 정확도가 향상되지 않으면 분할을 멈추고 해당 노드를 리프 노드(단말 노드)로 만듭니다.

• 장점:
  트리를 끝까지 만들지 않으므로 학습 속도가 빠릅니다.

• 단점:
  '탐욕적인(Greedy)' 접근법입니다. 지금 당장은 분할의 이득이 없어 보여도, 한 단계 더 깊이 분할하면 성능이 크게 향상될 수 있는 가능성을 놓칠 수 있습니다. 즉, 섣부른 판단으로 나무의 성장을 너무 일찍 멈출 위험이 있습니다.

2. 사후 가지치기 (Post-pruning)

• 개념: 일단 트리를 최대한 끝까지 성장시킨 후, 불필요한 가지를 아래에서부터 위로 올라오며 잘라내는 방식입니다.

• 동작 방식:
  1. 가장 아래쪽의 노드부터 검토하여, 특정 노드 아래의 하위 트리 전체를 하나의 리프 노드로 대체했을 때 검증 세트에서의 정확도가 향상되는지 확인합니다.
  2. 정확도가 향상되거나 거의 유지된다면, 과감하게 해당 하위 트리를 잘라내고 리프 노드로 만듭니다.
  3. 이 과정을 점차 위쪽 노드로 올라오며 반복합니다.

• 장점:
  모든 가능한 분할을 고려한 뒤에 가지치기를 하므로, 일반적으로 사전 가지치기보다 더 좋은 성능의 모델을 만듭니다.

• 단점:
  일단 트리를 끝까지 만들어야 하므로 학습 시간이 오래 걸리고 계산량이 많습니다.

4.4 연속값과 결측값

4.4.1 연속값

• 처리 문제 상황
  '밀도' 값은 0.243, 0.245, 0.351 등 무수히 많을 수 있습니다. 이 모든 값에 대해 가지를 만들 수는 없습니다.
• 해결책: 이분법 (Bi-partition)
  C4.5 알고리즘에서 사용하는 방법으로, 연속값을 하나의 분할점(cut-off point) t를 기준으로 두 개의 구간으로 나누는 것입니다. (예: "밀도 ≤ t인가?" 라는 이진 질문으로 바꿈)

어떻게 최적의 분할점 t를 찾을까?

1단계: 모든 후보 분할점 찾기

• 해당 속성(예: '밀도')의 모든 값들을 크기 순으로 정렬합니다. {a¹, a², ..., aⁿ}
• 인접한 두 값의 중간 지점들을 모두 후보 분할점으로 정합니다.
• 후보 분할점 집합 Tₐ 공식:
  

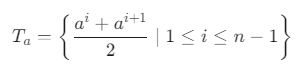
2단계: 정보 이득이 최대가 되는 분할점 선택

• 각각의 후보 분할점 t에 대해, 데이터 D를 ≤ t인 그룹과 > t인 그룹으로 나누고 정보 이득(Information Gain)을 계산합니다.
• 특정 분할점 t에 대한 정보 이득 공식
  
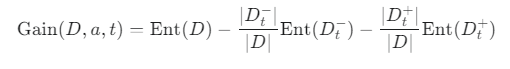
• 계산된 정보 이득 값들 중 가장 큰 값을 해당 연속 속성 a의 최종 정보 이득으로 선택합니다.
• 연속 속성 a의 최종 정보 이득 공식
  

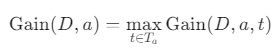
4.4.2 결측값 처리

문제 1: 속성값이 결측된 상황에서 어떻게 분할 속성을 선택할 것인가?

• 아이디어: 특정 속성에 결측값이 없는 데이터만 가지고 정보 이득을 계산한 뒤, 전체 데이터에서 해당 속성값이 존재하는 데이터의 비율을 곱하여 최종 정보 이득을 구합니다.

1단계: 데이터셋 분리

• D: 현재 노드의 전체 훈련 데이터셋
• D̃: 전체 D 중에서, 우리가 지금 평가하려는 속성 a에 결측값이 없는 데이터들의 부분집합.

2단계: 가중치(비율) ρ 계산

• ρ (로): 전체 데이터 중 속성 a의 값이 실제로 존재하는 데이터의 비율입니다.
  

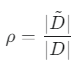
3단계: 정보 이득 계산

• 먼저, 결측값이 없는 데이터 D̃에 대해서만 표준 정보 이득 공식을 사용하여 Gain(D̃, a)를 계산합니다.
• 최종적으로, 위에서 구한 비율 ρ를 곱하여 가중치를 부여합니다.

결측값을 고려한 정보 이득 공식

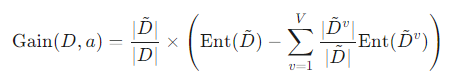
4.5 다변량 의사결정 트리

기존 의사결정 트리와의 차이점

• 일반 의사결정 트리 (Univariate): 각 노드에서 단 하나의 속성에 대한 질문을 합니다. (예: "색깔이 빨간색인가?" 또는 "밀도가 0.6보다 큰가?")
  • 이로 인해 만들어지는 결정 경계는 항상 축에 평행한(axis-parallel) 직선, 즉 계단 모양이 됩니다.
• 다변량 의사결정 트리 (Multivariate): 각 노드에서 여러 속성의 선형 결합에 대한 질문을 합니다. (예: "(0.7 x 밀도) + (0.3 x 당도)가 0.8보다 큰가?")
  • 이로 인해 만들어지는 결정 경계는 축에 평행하지 않은 사선(oblique) 형태가 될 수 있습니다.